НОУ ИНТУИТ | Введение в математику. Практикум. Лекция 3: Приложения дифференциального и интегрального исчисления

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3447 / 675 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Развитие исследовательских и творческих навыков по практическому использованию элементов дифференциального и интегрального исчисления

Ключевые слова: производная, интеграл, разложение в ряд, ряд, площадь

Какой экономический или социально–гуманитарный смысл можно придать производной и интегралу? Привести примеры. Указание: экономическим смыслом может быть, например, темп производства (если дифференцируемой функции придать смысл функции производства, объема выпущенной продукции).
Пусть интенсивность реализации (выпуска) продукции на заводе равна 500 ед./год, затраты на запуск в производство партии продукции 2000 руб., себестоимость 1 единицы продукции – 1000 руб., а стратегия управления состоит в том, чтобы получить отдачу 2 руб. на каждый 1 руб. вложенный в запасы денежных средств в год. Найти минимум общих затрат. Указание: выписать функцию цели – стоимость общих затрат.
Пусть 100 лет назад в Австралию (с идеальными условиями обитания и отсутствием хищников) было завезено 1000 кроликов. Условно коэффициент прироста k=0.5 (пять кроликов на десять кроликов). Найти количество кроликов через 10 лет такой "хорошей жизни" кроликов. Построить модель динамики их роста. Указание: прирост кроликов определяется производной, а закон роста – экспоненциальный (нет лимитирования).
Интенсивность изучения иностранных слов определяется производной от x(t), где t – время, x(t) – объем слов, изученных к моменту времени t. Максимальный словарный запас равен X. Записать уравнение динамики (темпа) изучения слов. Указание: использовать простую гипотезу – темп изучения пропорционален объему неизученных слов.
Железная дорога для подвоза сырья описывается на некотором участке уравнением x+2y=3, а железная дорога для поставки готовой продукции – уравнением 5x–2y=2. Река, ограничивающая местность возможной постройки завода на этом участке можно описывать уравнением y=0. По этой реке также подвозится часть сырья. В какой точке можно построить завод, чтобы стоимость подвоза сырья и отвоза продукции была бы минимальной? Указание: сделать чертеж, выписать функцию цели – сумма расстояний до дорог.
Найти натуральное число е с погрешностью не более 0,001, используя разложение экспоненциальной функции в ряд Маклорена. Указание: подсчитать сумму элементов ряда Маклорена для экспоненты при х=1 до тех пор, пока добавляемое новое слагаемое не станет меньше 0,001.
Вычислить значение интеграла

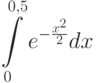
$\int\limits_0^{0,5}{e^{-\frac{x^2}{2}}dx}$

приближенно (с точностью 0,01 ), используя разложение в ряд подынтегральной функции (вместо x в разложение подставляем – x²/2 ). Оценить погрешность вычисления. Указание: подставить вместо интегрируемой функции ее разложение в ряд Маклорена и "оборвать" сумму интегралов на первом слагаемом ( интеграле ), который меньше 0,01.
Пусть производная по х характеризует скорость изменения потока в зависимости от увеличения или уменьшения числа жителей х, а производная по y характеризует скорость изменения потока в зависимости от увеличения или уменьшения расстояния y между пунктами: 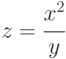$z=\cfrac{x^2}{y}$ . Получите (обоснуйте) закон: уменьшение потока пассажиров обратно пропорционально квадрату расстояния между пунктами, при одной и той же численности жителей в пунктах, а увеличение потока пассажиров пропорционально числу жителей населенных пунктов при одном и том же расстоянии между пунктами. Указание: вычислить первые частные производные функции z и найдите между ними зависимость ("свяжите их").
Найти значение корня $\sqrt[3]{0,98\sqrt[4]{1,05^3}}$ используя равенство вида:

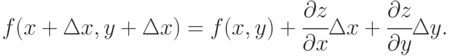
$f(x+\Delta x, y+\Delta x) = f(x,y) + \cfrac{ \partial z}{ \partial x} \Delta x + \cfrac{ \partial z}{ \partial y} \Delta y.$

Указание: взять следующие параметры равенства: x=1, y=1, $\Delta x=-0,02$ , $\Delta y=0,05$ .
Определить, какая площадь больше (и на сколько): площадь фигуры, ограниченной линиями y=x² , y=x²+2 или площадь фигуры, ограниченной линиями y=x³ , y=x. Указание: сделайте эскизы графиков, искомой площади и найдите точки пересечения линий; площадь вычислить с помощью интеграла (от "верхней" функции отнять "нижнюю").

Дальше >>

Авторизоваться

Введение в математику. Практикум

Приложения дифференциального и интегрального исчисления

Вопросы и ответы