Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3435 / 667 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00
Тема: Математика
Специальности: Математик
Теги:
Практическая работа 8:
Дифференцирование
< Практическая работа 7 || Практическая работа 8 || Практическая работа 9 >
Аннотация: Решение типовых задач дифференциального исчисления функции одной и нескольких переменных, обучение реферированию и Интернет–поиску по этой теме
Задачи
-
Исходя лишь из определения производной, найти производную функции вида:
-
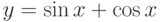 ;
; -
 ;
; -
 .
.
Указание: оценить отношение

-
-
-
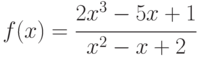 ;
; -
 ;
; -
 .
.
Указание: использовать формулы дифференцирования суммы, разности, произведения, дроби и таблицу производных.
-
-
-
 ;
; -
 ;
; -
 .
.
Указание: использовать формулы дифференцирования сложной функции, суммы, разности, произведения, дроби и таблицу производных.
-
- Найти частные производные до второго порядка включительно для функции z=x2y-xy2+5ln(x+y). Указание: использовать формулы uxx=(ux)x, uyy=(uy)y, uxy=uyx= (ux)y=(uy)x.
- Найти промежутки возрастания и убывания, точки перегиба и экстремума функции y=e—x+ex. Указание: это значения х, для которых, соответственно, y/>0, y/<0, y/=0.
- Найти экстремум, наибольшее и наименьшее значения функции y=sinx+cosx на промежутке [0;5). Указание: так как х<5, то y(5) вычислять не нужно.
-
Найти экстремум, наибольшее и наименьшее значения функции

на отрезке [0;1]. Указание: исследовать тип экстремума в критической точке.
- Исследовать по полной схеме исследования функцию вида: y=2—3x+x2. Указание: найти области D(y), E(y), монотонности, периодичности, разрывы, перегибы, экстремумы, асимптоты, поострить график (эскиз).
- Исследовать по полной схеме исследования функцию вида: y=3e-2x+ex. Указание: найти области D(y), E(y), монотонности, периодичности, разрывы, перегибы, экстремумы, асимптоты, поострить график (эскиз).
- Исследовать по полной схеме исследования функцию вида: y=ln(x2+1). Указание: найти области D(y), E(y), монотонности, периодичности, разрывы, перегибы, экстремумы, асимптоты, поострить график (эскиз).
Темы научных исследований и рефератов (Интернет-листов)
- Производная, ее происхождение.
- Различные смыслы (геометрический, физический, экономический и др.) производной.
- Исторические предпосылки формирования элементов дифференциального исчисления.
- Дифференциальное исчисление и его эволюция.
- Приложения дифференцирования в социально-экономических областях.
- Приложения дифференцирования в гуманитарных областях.
- Дифференцирование функции многих переменных.
- Экстремумы функций и их приложения.
- Методы дифференцирования.
- Фундаментальность дифференциального исчисления как метода исследования законов природы и общества.
< Практическая работа 7 || Практическая работа 8 || Практическая работа 9 >
