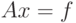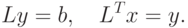Опубликован: 18.05.2011 | Доступ: свободный | Студентов: 965 / 104 | Оценка: 4.40 / 4.20 | Длительность: 12:30:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги:
Лекция 14:
Нелиненйые уравнения
Лабораторная работа "Решение линейных и нелинейных уравнений"
Цель занятия
Аппробировать базовые численные методы для решения систем линейных алгебраических уравнений и нелинейных трансцендентных уравнений.
Сценарий лабораторной работы
- Написать программу на языке C# для нахождения разложения
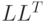 по методу Холецкого для симметричных положительно определенных
матриц. Провести различные вычислительные опыты.
по методу Холецкого для симметричных положительно определенных
матриц. Провести различные вычислительные опыты. - Напишите программу для решения системы линейных алгебраических уравнений для симметричных положительно определенных матриц на основе метода Холецкого.
- Реализовать метод Ньютона для приближенного решения уравнения
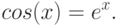
- Найти теоретические границы сходимости итераций Ньютона для этого уравнения.
Указания
Метод Холецкого позволяет найти такую матрицу  , которая имеет
вид
, которая имеет
вид
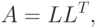
 - нижняя треугольная матрица
- нижняя треугольная матрица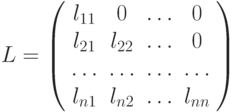
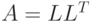 , то уравнение
, то уравнение