Обыкновенные дифференциальные уравнения
Цель лекции: Показать эффективность объектно-ориентированного подхода к задаче нахождения численных решений задачи Коши для дифференциальных уравнений. Провести вычислительные эксперименты и сравнить различные методы.
В настоящей лекции мы будем рассматривать задачу Коши для довольного широкого класса обыкновенных дифференциальных уравнений.
Сначала перейдем к формальному определению постановки задачи
Коши. Пусть  - область (ограниченная или нет) в
- область (ограниченная или нет) в  -мерном пространстве. Пусть также задан отрезок
-мерном пространстве. Пусть также задан отрезок ![[0,\Bbb{T}]](/sites/default/files/tex_cache/04ac6f9a8a5ac4ef16981c5e9a0b710f.png) ,
здесь
,
здесь  может быть и бесконечностью. Введем обозначение
может быть и бесконечностью. Введем обозначение
![D_\Bbb{T}=\{(x,t):x\in\overline D,t\in[0,\Bbb{T}]\}.](/sites/default/files/tex_cache/0c895a8a55b47f5d21d805f45da38170.png)
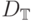 задана функция
задана функция 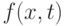 тогда можно рассматривать
обыкновенное дифференциальное уравнение
тогда можно рассматривать
обыкновенное дифференциальное уравнение![y'(t)=f(y(t),t),\ t\in[0,\Bbb{T}].](/sites/default/files/tex_cache/35ef3fa585522679451ce52753862dd7.png) |
( 16.1) |
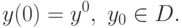 |
( 16.2) |
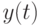 такой, что на некотором интервале
такой, что на некотором интервале ![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) функция
функция 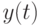 имеет непрерывную производную при
имеет непрерывную производную при ![t\in[0,T]](/sites/default/files/tex_cache/8b20560d8c06799d96af194ac2594a0b.png) имеет место
имеет место  , и функция
, и функция 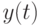 удовлетворяет уравнению 16.1 и начальному условию
16.2.
удовлетворяет уравнению 16.1 и начальному условию
16.2.В теории обыкновенных дифференциальных уравнений доказываются следующие теоремы.
Теорема 16.1. Пусть функция 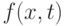 является непрерывной в
является непрерывной в 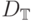 , тогда
существует такое
, тогда
существует такое  , что на
, что на ![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) существует по крайней мере
одно решение задачи 16.1-16.2.
существует по крайней мере
одно решение задачи 16.1-16.2.
В условиях теоремы существуют примеры задач Коши, которые имеют
более одного решения. Действительно, если взять  ,
,  , а в качестве функции
, а в качестве функции 
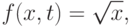

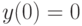
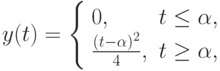
 - параметр семейства решений.
- параметр семейства решений.Чтобы гарантировать единственность решения задачи Коши, необходимо
накладывать большие условия на функцию  .
.
Теорема 16.2. Пусть функция 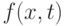 является непрерывной в
является непрерывной в 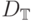 , и
существует такая положительная константа
, и
существует такая положительная константа  , зависящая только
от
, зависящая только
от  что для любого отрезка
что для любого отрезка ![[0,\tau]\subset[0,\Bbb{T}]](/sites/default/files/tex_cache/56a7442d3783c6a4d2810b59a6385bc6.png) выполнено неравенство
выполнено неравенство
 |
( 16.3) |
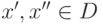 и
и ![t\in[0,\tau]](/sites/default/files/tex_cache/9b7a68a8c422f3640411e8db4ac0d10f.png) .
.Тогда существует такое  , что на
, что на ![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) существует
единственное решение задачи 16.1-16.2.
существует
единственное решение задачи 16.1-16.2.
Условие 16.3 называется условием Липшица. Это
условие будет заведомо выполнено, если непрерывная функция  имеет ограниченные и непрерывные производные по
имеет ограниченные и непрерывные производные по 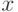 в
в 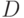 .
.
Приведенные выше теоремы гарантируют только локальную разрешимость
задачи Коши. Действительно, следующий пример задачи Коши не имеет
решения на любом отрезке ![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) , где
, где 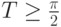 . Пусть
снова
. Пусть
снова  , функция
, функция 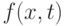 имеет вид
имеет вид
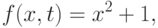
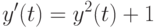


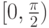 .
.Чтобы гарантировать существование глобального по времени решения, необходимо накладывать дополнительные условия на рост правой части.
Теорема 16.3. Пусть выполнены все условия теоремы 16.2 и дополнительно
функция 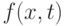 удовлетворяет условию в области
удовлетворяет условию в области 
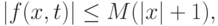
 не зависит ни от
не зависит ни от 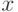 , ни от
, ни от 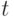 , тогда задача
Коши имеет единственное решение на отрезке
, тогда задача
Коши имеет единственное решение на отрезке  .
.В курсах по обыкновенным дифференциальным уравнениям проходят разнообразные методы нахождения точных решений дифференциальных уравнений. Однако, во-первых, случаи, когда можно найти точные решения являются исключительными случаями и для многих уравнений доказано, что найти решение в квадратурах невозможно. Во-вторых, даже если удалось найти точное решение, то это решение может быть выражено в неявном виде, либо в виде квадратур, которые в свою очередь могут не выражаться в элементарных случаях. В-третьих, во многих задачах правые части могут не быть заданы элементарными функциями. Наконец, во многих случаях построение приближенного решения с достаточной точностью является значительно более простым и эффективным, чем нахождение точного решения.
