Принципы организации вычислительных процедур
Цель лекции: Показать важность правильности выбора вычислительных процедур. Продемонстрировать итерационные вычислительные процедуры на простом примере программы на C#.
К классическим темам вычислительной математики обычно относят следующие разделы:
- Табулирование функций и интерполяция
- Нахождения корней систем уравнений
- Решение задач линейной алгебры
- Численное интегрирование и дифференцирование
- Решение обыкновенных дифференциальных уравнений (задачи Коши и краевых задач)
- Решение уравнений в частных производных
- Решение интегральных уравнений
- Задачи линейного и нелинейного программирования
- Обработка результатов экспериментов и задачи математической статистики
- Решение задач дискретной математики
Разумеется, это не полный список тем вычислительной математики, поскольку практически в любой области математики можно найти "работу" для численных методов. Среди собственных тем вычислительной математики можно выделить следующие:
- Сходимость численных методов
- Оценка погрешности и сложности вычислительных процедур
- Программирование численных методов
- Методика проведения вычислительных экспериментов
Рассмотрим принципы организации вычислительных процедур на примере
решения операторного уравнения. Пусть  и
и  метрические
пространства с метриками
метрические
пространства с метриками 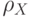 и
и  соответственно, и
пусть задано однозначное отображение
соответственно, и
пусть задано однозначное отображение
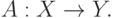
![A[x]=y,](/sites/default/files/tex_cache/2a916d7ffa110228aa764bc25a02af9d.png) |
( 5.1) |
 .
.Решением уравнения 5.1 называется элемент 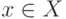 ,
удовлетворяющий уравнению 5.1. Мы будем предполагать,
что существует хотя бы одно решение уравнения 5.1,
которое мы обозначим через
,
удовлетворяющий уравнению 5.1. Мы будем предполагать,
что существует хотя бы одно решение уравнения 5.1,
которое мы обозначим через 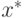 . Задачей вычислительной
математики является конструктивное построение такого отображения
. Задачей вычислительной
математики является конструктивное построение такого отображения
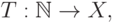
![x_n=T[n]](/sites/default/files/tex_cache/e90b8f46d2ae37f6808f0d0bfc951acf.png)
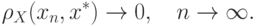
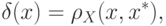
![\varepsilon(x)=\rho_Y(A[x],y).](/sites/default/files/tex_cache/30acfeba1b8a0d70025ba6179394aa46.png)
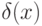 необходимо знать собственно
решение
необходимо знать собственно
решение 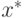 , что возможно лишь в тестовых задачах. С другой
стороны при вычислении невязки решение не участвует, поэтому
величина
, что возможно лишь в тестовых задачах. С другой
стороны при вычислении невязки решение не участвует, поэтому
величина 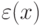 является конструктивно вычисляемой.
является конструктивно вычисляемой.Как правило, целью численных методов является построение такой
последовательности 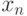 , для которой выполнено условие:
, для которой выполнено условие:
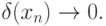
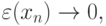
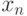 сходится к
решению (и вообще, что сходится). Рассмотрим простой пример. Пусть
сходится к
решению (и вообще, что сходится). Рассмотрим простой пример. Пусть 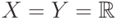 - числовая ось. Функция
- числовая ось. Функция  задана по формуле:
задана по формуле:![A[x]=\frac{x^2}{1+x^4}.](/sites/default/files/tex_cache/6f823df1be4976007881fd57a403d656.png)
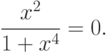
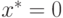 . Если мы
используем вычислительную процедуру
. Если мы
используем вычислительную процедуру![x_n=T[n]=\frac{1}{n},](/sites/default/files/tex_cache/82c4226fbc78f0a9de3e3b3237f22e8d.png)
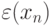 имеет вид
имеет вид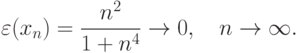
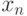 никак не сходится к решению.
Заметим, что причиной такой ситуации является то, что пространство
никак не сходится к решению.
Заметим, что причиной такой ситуации является то, что пространство  , на котором задана функция
, на котором задана функция  , не является компактным.
, не является компактным.Однако есть следующая зависимость между функциями 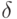 и
и  . Если предположить, что отображение
. Если предположить, что отображение  является
непрерывным отображением, то для любой последовательности
является
непрерывным отображением, то для любой последовательности 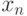 из
условия
из
условия