Oбъектно-opиентированное управление решениями дифференциальных уравнений
Цель лекции: Показать применение дифференциальных уравнений в задачах управления. Показать эффективность объектно-ориентированного управления в задачах построения управляемых систем.
Многие процессы, описываемые дифференциальными уравнениями, являются управляемыми системами. Дадим формальное описание управляемой системы.
Пусть  ,
, 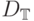 имеют тот же смысл, что и в прошлой лекции.
Пусть теперь еще выделено семейство множеств
имеют тот же смысл, что и в прошлой лекции.
Пусть теперь еще выделено семейство множеств  ,
где
,
где  и
и ![t\in[0,\Bbb{T}]](/sites/default/files/tex_cache/3de74289177305d93af1d0c857664f88.png) являются параметрами. Множество
являются параметрами. Множество  называется множеством допустимых управлений.
называется множеством допустимых управлений.
Пусть теперь задана функция  , которая определена при
, которая определена при  ,
, ![u\in\bigcup\limits_{x\in\overline{D},t\in[0,\Bbb{T}]}U(x,t)](/sites/default/files/tex_cache/c6a216b20b51baea97b560154e9fbd87.png) ,
, ![t\in[0,\Bbb{T}]](/sites/default/files/tex_cache/3de74289177305d93af1d0c857664f88.png) . Будем рассматривать обыкновенное дифференциальное
уравнение с управлением
. Будем рассматривать обыкновенное дифференциальное
уравнение с управлением
![\begin{array}{c}
y'(t)=f(y(t),u(t),t), \\
\\
u(t)\in U(y(t),t)\ t\in[0,\Bbb{T}].\\
\end{array}](/sites/default/files/tex_cache/157b0259ed97a195a9197dfd5265bf1e.png) |
( 18.1) |
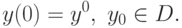 |
( 18.2) |
![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) является
измеримая функция
является
измеримая функция 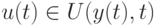 и абсолютно непрерывная
функция
и абсолютно непрерывная
функция  ,
, ![t\in[0,T]](/sites/default/files/tex_cache/8b20560d8c06799d96af194ac2594a0b.png) , и эти функции
удовлетворяют 18.1-18.2.
, и эти функции
удовлетворяют 18.1-18.2.Мы сформулировали задачу на управления решениями дифференциальных уравнений в довольно общем виде. Однако, как правило, управление осуществляется с некоторой целью. Для этого вводится так называемый целевой функционал. Целевым функционалом называется любая числовая функция определенная на решении задачи 18.1-18.2. Обозначим этот функционал следующим образом
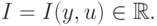
 и
и  является удовлетворительным с точки зрения
целевого функционала, если
является удовлетворительным с точки зрения
целевого функционала, если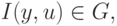
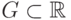 называется удовлетворительной областью значения
целевого функционала. Заметим, что
называется удовлетворительной областью значения
целевого функционала. Заметим, что  может быть произвольным
непустым множеством.
может быть произвольным
непустым множеством.Обратимся к моделированию задач управления. Общая схема такова
- Задаем начальное управление
- Решаем систему дифференциальных уравнений с начальным управлением на одном шаге методом Рунге-Кутты
- По полученному решению на очередном шаге меняем (в случае необходимости) управление
- Повторяем шаги 2-3 до тех пор пока решение и управления не станут удовлетворительными с точки зрения целевого функционала
Следует отметить, что далеко не всегда удовлетворительное с точки зрения целевого функционала решение задачи управления является оптимальным решением. Более того, существует такие задачи управления решениями, для которых не существует оптимального решения.
Реализуем эту схему в виде абстрактного класса, который мы
создадим, как наследник класса  .
.
![\begin{verbatim}
abstract class TControlSystem : TRungeKutta
{
public int M;
public double[] U;
public TControlSystem(int N, int M) : base(N)
{
this.M = M;
U = new double[M];
}
abstract public void SetU();
public override void NextStep(double dt)
{
SetU();
base.NextStep(dt);
}
}
\end{verbatim}](/sites/default/files/tex_cache/0b635740ffff042d3d76c95e5f9858d6.png)
Рассмотрим модельную систему управления на основе уравнений, описывающих математический маятник. Будем рассматривать следующую управляемую систему дифференциальных уравнений.
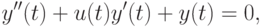


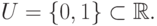
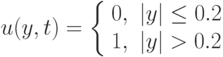
![\begin{verbatim}
class TOscControl : TControlSystem
{
public TOscControl() : base(2, 1)
{
U[0] = 0;
}
public override void SetU()
{
if (Math.Abs(Y[0]) > 0.2)
{
U[0] = 1;
}
else
{
U[0] = 0;
}
}
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = Y[1];
FY[1] = -Y[0] - U[0] * Y[1];
}
}
\end{verbatim}](/sites/default/files/tex_cache/3d644d888345636bbbda476a99793e04.png)
И проведем вычислительный эксперимент.
![\begin{verbatim}
TOscControl Osc = new TOscControl();
Osc.SetInit(0, new double[2] { 1, 0 });
double h = 0.01;
StreamWriter F = File.CreateText("control.txt");
while (Osc.GetCurrent() < 50.0 + h / 2.0)
{
Console.WriteLine("{0}\t{1}\t{2}\t{3}",
Osc.GetCurrent(), Osc.Y[0], Osc.Y[1], Osc.U[0]);
F.WriteLine("{0}\t{1}\t{2}\t{3}",
Osc.GetCurrent(), Osc.Y[0], Osc.Y[1], Osc.U[0]);
Osc.NextStep(h);
}
F.Close();
\end{verbatim}](/sites/default/files/tex_cache/f7537242bddb290c7b43265643532889.png)
