Нейросетевые информационные модели сложных инженерных систем
Прикладное информационное моделирование в задаче оценки риска при эксплуатации сложной инженерной системы
Сложные инженерные устройства при воздействии внешних факторов могут демонстрировать разнообразное нелинейное поведение. С точки зрения эксплуатации таких систем отклик может отвечать нормальному режиму работы, а также аномальным и аварийным режимам. В последнем случае требуется принятие специальных мер для снижения риска последствий инцидента.
Задача информационного моделирования при оценке риска 12Проблема оценивания самой величины риска при этом остается за рамками данного рассмотрения. Одним из методов вычисления риска при известных из информационного или математического моделирования режимах работы системы является взвешивание вероятностей реализации различных режимов с экспертными оценками их последствий. Далее управление эксплуатацией системы состоит в минимизации риска. для объекта при внешнем нагружении состоит в необходимости предсказания его поведения в обычных и аномальных условиях.
Описание инженерной системы
Примером задачи оценки риска является эксплуатация контейнера для перевозки или хранения промышленных отходов (например, делящиеся материалы в отработанных твэлах атомных электростанций, или токсичные химические вещества). В качестве аномального внешнего воздействия требуется рассмотрение пожара с различными параметрами. Отклик контейнера (измеряемый оценкой сохранности содержимого и не проникновением его во внешнюю среду) может изменяться в зависимости от текущего состояния системы, например, степенью возможных повреждений в аварийных условиях.
Рассмотрим относительно простую и полезную с практической точки зрения модель, основанную на данных измерений параметров контейнера при различных условиях пожара. Фактически, построенная модель основывалась на результатах численного моделирования, а не на реальных данных. Это, однако, не снижает ценность рассмотрения, поскольку в численных расчетах удается учесть широкий спектр пожаров для одного и того же контейнера. Неопределенность в коэффициентах, описывающих теплофизические свойства материалов, а также численные эффекты, вносят шум в используемые данные, приближая условия моделирования к реальным. В сложившейся практике нейросетевого моделирования данные такого рода называют реалистичными (в отличие от искусственных и реальных данных).
База собранных данных содержит 8 параметров, описывающих контейнер и условия пожара. Признаковое пространство входов состоит из 6 переменных - одной переменной состояния контейнера (экспертная оценка степени повреждения контейнера) и пяти параметров воздействия (свойств пожара).
Параметры пожара включают две координаты области пламени, диаметр этой области, температуру пожара и его длительность.
Двумя выходными переменными являются максимальное значение температуры внутри контейнера на протяжении всего пожара, а также отрезок времени, в течение которого температура внутри контейнера превышала некоторое пороговое значение, соответствующее критическому уровню возможного повреждения содержимого контейнера.
Нейросетевая информационная модель системы
Информационная модель отклика контейнера строилась на основе сети встречного распространения и многослойной сети с обучением по методу обратного распространения ошибки. Были рассмотрены прямая, обратная и комбинированная задачи.
Нейронная сеть для прямой задачи содержит 6 входов и 2 оцениваемых выхода. Прямая задача для данного приложения позволят ответить на следующие вопросы:
- Какова будет максимальная температура внутри контейнера при известных параметрах пожара?
- Превысит или нет внутренняя температура заданное критическое значение? Если да, то как долго система будет находиться в критических условиях?
- Что отвечает большему риску повреждения содержимого контейнера: короткий, но высокотемпературный пожар, или длительная умеренная тепловая нагрузка?
Обратная задача соответствует оценке параметров внешнего воздействия по измерениям отклика системы. Тепловой режим внутри контейнера при этом контролируется датчиками температуры. Запросы к обратной модели носят диагностический характер:
- Какова длительность и температура пламени?
- Как далеко от контейнера произошел пожар, и каков был размер пламени?
- Какова фактическая степень повреждения контейнера?
Наиболее интересная комбинированная задача рассматривает часть параметров как известные, а остальные, как неизвестные. При обучении нейросети комбинированной задаче множества переменных, используемых как входные и как выходные, могут частично или полностью перекрываться.
Комбинированная задача отвечает на все запросы прямой и обратной задач, но имеет дополнительные возможности:
- Оценка состояния контейнера по внешним и внутренним измерениям.
- Каковы наитяжелейшие условия пожара, при которых контейнер еще сохраняет содержимое?
Обратную и комбинированную задачи следует рассматривать, как некорректно поставленные.
Область возможных значений физических параметров ограничивалась максимальными температурами пожара (достигаемыми при горении обогащенного топлива), расстояниями и размерами пламени, при которых теплопередача контейнеру приводит к температуре около 200оС (типичный порог для пожаро-сигнализирующих датчиков). Длительность пожара ограничивалась значением 1 час.
После введения всех ограничений данные из базы данных были линейным преобразованием приведены в "серый" формат [0..1].
Интегральная оценка корректности модели
На первом этапе в предлагаемой технологии исследовалась корректность задачи на всей области значений параметров. С этой целью последовательно выбирались семь параметров из восьми, включенных в модель. Эти параметры считались известными, а оставшийся восьмой параметр - неизвестным. Таким образом, каждый из параметров по очереди тестировался, как неизвестный. При моделировании определялась ошибка обучения многослойной сети с обратным распространением. Все расчеты проводились для нейросетей большого13Для определения необходимого числа нейронов на скрытом слое была выполнена серия расчетов с увеличивающимся размером сети. Далее использовалось полученное предельное значение (для нашей базы данных из  примеров потребовалось 30 нейронов).
размера, поэтому полученная ошибка связывается только с некорректностью задачи. Был использован следующий вид функции ошибки (называемой процентом среднего квадрата ошибки 14Исходный английский термин - squared error percentage .
):
примеров потребовалось 30 нейронов).
размера, поэтому полученная ошибка связывается только с некорректностью задачи. Был использован следующий вид функции ошибки (называемой процентом среднего квадрата ошибки 14Исходный английский термин - squared error percentage .
):
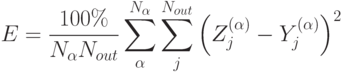
Численное моделирование показало, что обе прямые задачи, когда неизвестными считались выходные переменные задачи - максимальная температура внутри контейнера и длительность периода превышения заданного уровня температуры, являются корректно поставленными. Значение ошибки обучения не превышало 1%. Напротив, все шесть обратных/комбинированных задач оказались некорректными с ошибкой обучения масштаба 25-35%. Данные результат является принципиальным для планирования последующих экспериментов с информационной моделью: попытки оценки решения обратных задач на всей области значений (без дифференциального анализа корректности) будут неудачными.

