Лекция 9: Логически прозрачные нейронные сети и производство явных знаний из данных
Вычислительный центр СО РАН в г. Красноярске
Производство явных знаний из накопленных данных - проблема, которая намного старше чем компьютеры. Обучаемые нейронные сети могут производить из данных скрытые знания: создается навык предсказания, классификации, распознавания образов и т.п., но его логическая структура обычно остается скрытой от пользователя. Проблема проявления (контрастирования) этой скрытой логической структуры решается в работе путем приведения нейронных сетей к специальному "логически прозрачному" разреженному виду.
Исследуются два вопроса, встающие перед каждым исследователем, решившим использовать нейронные сети: "Сколько нейронов необходимо для решения задачи?" и "Какова должна быть структура нейронной сети?" Объединяя эти два вопроса, мы получаем третий: "Как сделать работу нейронной сети понятной для пользователя (логически прозрачной) и какие выгоды может принести такое понимание?" Описаны способы получения логически прозрачных нейронных сетей. Приведен пример из области социально-политических предсказаний. Для определенности рассматриваются только нейронные сети, обучение которых есть минимизация оценок (ошибок) с использованием градиента. Градиент оценки вычисляется методом двойственности (его частный случай - метод обратного распространения ошибки).
Сколько нейронов нужно использовать?
При ответе на этот вопрос существует две противоположные точки зрения. Одна из них утверждает, что чем больше нейронов использовать, тем более надежная сеть получится. Сторонники этой позиции ссылаются на пример человеческого мозга. Действительно, чем больше нейронов, тем больше число связей между ними, и тем более сложные задачи способна решить нейронная сеть. Кроме того, если использовать заведомо большее число нейронов, чем необходимо для решения задачи, то нейронная сеть точно обучится. Если же начинать с небольшого числа нейронов, то сеть может оказаться неспособной обучиться решению задачи, и весь процесс придется повторять сначала с большим числом нейронов. Эта точка зрения (чем больше - тем лучше) популярна среди разработчиков нейросетевого программного обеспечения. Так, многие из них как одно из основных достоинств своих программ называют возможность использования любого числа нейронов.
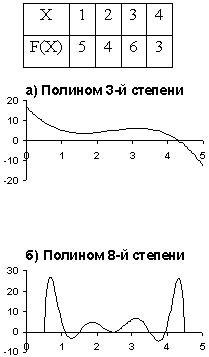
Вторая точка зрения опирается на такое "эмпирическое" правило: чем больше подгоночных параметров, тем хуже аппроксимация функции в тех областях, где ее значения были заранее неизвестны. С математической точки зрения задачи обучения нейронных сетей сводятся к продолжению функции заданной в конечном числе точек на всю область определения. При таком подходе входные данные сети считаются аргументами функции, а ответ сети - значением функции. На рис. 9.1 приведен пример аппроксимации табличной функции полиномами 3-й ( рис. 9.1.а ) и 8-й ( рис. 9.1.б ) степеней. Очевидно, что аппроксимация, полученная с помощью полинома 3-ей степени больше соответствует внутреннему представлению о "правильной" аппроксимации. Несмотря на свою простоту, этот пример достаточно наглядно демонстрирует суть проблемы.
Второй подход определяет нужное число нейронов как минимально необходимое. Основным недостатком является то, что это, минимально необходимое число, заранее неизвестно, а процедура его определения путем постепенного наращивания числа нейронов весьма трудоемка. Опираясь на опыт работы группы НейроКомп в области медицинской диагностики [9.4,9.5,9.9], космической навигации и психологии [9.10] можно отметить, что во всех этих задачах ни разу не потребовалось более нескольких десятков нейронов.
Подводя итог анализу двух крайних позиций, можно сказать следующее: сеть с минимальным числом нейронов должна лучше ("правильнее", более гладко) аппроксимировать функцию, но выяснение этого минимального числа нейронов требует больших интеллектуальных затрат и экспериментов по обучению сетей. Если число нейронов избыточно, то можно получить результат с первой попытки, но существует риск построить "плохую" аппроксимацию. Истина, как всегда бывает в таких случаях, лежит посередине: нужно выбирать число нейронов большим чем необходимо, но не намного. Это можно осуществить путем удвоения числа нейронов в сети после каждой неудачной попытки обучения. Однако существует более надежный способ оценки минимального числа нейронов - использование процедуры контрастирования [9.1]. Кроме того, процедура контрастирования позволяет ответить и на второй вопрос: какова должна быть структура сети.