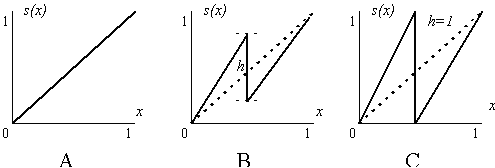Нейросетевые информационные модели сложных инженерных систем
Прямые, обратные и комбинированные задачи информационного моделирования
При формулировании постановки информационной задачи предсказания реакции исследуемой системы при ее известном состоянии на заданные внешние воздействия, т.е. получения величин Y при заданных X исследователь имеет дело с прямой задачей. Прямая задача является типичной при моделировании поведения системы, если запросы к информационной модели носят характер что-если.
Другим важным классом информационных задач являются обратные задачи. Целью обратной задачи выступает получение входных величин X, соответствующих наблюдаемым значениям выходов Y. При моделировании сложных систем соответствующий запрос к модели формулируется, как поиск внешних условий, которые привели к реализовавшемуся отклику системы.
Для большинства приложений чисто обратные задачи встречаются относительно редко, так как обычно имеются дополнительные сведения о системе. Например, кроме измеренного отклика, могут быть известны переменные состояния системы и часть параметров воздействия. В этом случае задача относится к классу комбинированных задач: по известным значениям части компонент входного X и выходного Y векторов восстановить оставшиеся неизвестные компоненты.
В общем случае моделируемая системная функция может быть представлена в виде (X,Y)=F (X, Y). В этом случае комбинированный вектор (X,Y) рассматривается одновременно, как входной и выходной. В этом смысле, произвольная задача допускает комбинированную постановку.
Некорректность обратной задачи
Отличительная особенность обратных и комбинированных задач состоит в том, что они обычно являются некорректно поставленными [4.10], и поэтому требуют специализированных методов поиска приближенных решений. Согласно Ж.Адамару, для корректности постановки задачи необходимо:
- существование решения при всех допустимых исходных данных;
- единственность данного решения;
- устойчивость решения к изменениям (малым) исходных данных.
Рассмотрим характер возможных нарушений данных условий при решении модельной обратной задачи.
Пусть имеется три исследуемых систем, описываемых кусочно-линейными функциями одной переменной y=F(x) на отрезке [0..1]. Системы отличаются друг от друга величиной скачка h системной функции (см рис. 4.2). Прямая задача состоит в построении приближения G к функции F, с использованием пар значений {xi, yi=s(xi)}, где xi - конечный набор Na случайных равномерно распределенных на [0..1] точек. Обратная задача заключается в нахождении функции, аппроксимирующей соотношения xi(yi). В зависимости от величины скачка моделируемой функции можно выделить три варианта.
-
Система A ( h=0 ). Модель является линейной: y=x. Для прямой задачи легко получить исчезающую ошибку обучения
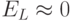 , и малую8Это достигается, например, использованием нейронной сети без скрытых слоев с произвольной переходной функцией нейронов, имеющей близкий к линейному участок изменения.
ошибку обобщения EG. Для обратной задачи получаются такие же результаты, так она при точных значения {xi, yi} не содержит некорректности. Задачи с решениями, корректными на всей области определения и множестве значений, будем называть безусловно корректными. Корректность постановки обратной задачи для системы А определяется существованием однозначной и непрерывной функции F-1.
, и малую8Это достигается, например, использованием нейронной сети без скрытых слоев с произвольной переходной функцией нейронов, имеющей близкий к линейному участок изменения.
ошибку обобщения EG. Для обратной задачи получаются такие же результаты, так она при точных значения {xi, yi} не содержит некорректности. Задачи с решениями, корректными на всей области определения и множестве значений, будем называть безусловно корректными. Корректность постановки обратной задачи для системы А определяется существованием однозначной и непрерывной функции F-1.
-
Система B ( 0<h<1 ). Прямая задача в этом случае также хорошо определена, и при использовании достаточно богатого множества базисных функций можно произвольно уменьшить ошибку обучения (
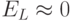 ) при хорошем обобщении. Обратная задача характеризуется наличием на множестве значений областей с однозначной ( y > 0.5+0.5h; y < 0.5-0.5h ) и неоднозначной (
) при хорошем обобщении. Обратная задача характеризуется наличием на множестве значений областей с однозначной ( y > 0.5+0.5h; y < 0.5-0.5h ) и неоднозначной ( ![{\rm{y }}\in {\rm{[0}}{\rm{.5 - 0}}{\rm{.5h}}{\rm{, 0}}{\rm{.5 + 0}}{\rm{.5h]}}](/sites/default/files/tex_cache/1ad7df4f90b1af7222ad70df8fdb1224.png) ) обратной функцией. В областях однозначности функции могут быть получены произвольно точные результаты для обратной задачи. Однако в отрезке нарушения однозначности ошибка обучения (и ошибка обобщения) останется конечной, поскольку противоречие в данных, полученных из разных ветвей обратной функции, не устранимо. Значение ошибки обобщения пропорционально длине отрезка неоднозначности h. Такие задачи, корректное (единственное и устойчивое) решение которых может быть получено только для
некоторой подобласти множества значений, будем называть условно (или частично ) корректными9В книге [4.1], стр. 563, условно-корректными названы задачи, в постановку которых добавлено априорное предположение о существовании решения на некотором компакте. Для данного решения должна быть доказана теорема единственнности. В нашем рассмотрении в качестве такого компактного множества выступают отрезки, на которых обратная функция однозначна.
.
) обратной функцией. В областях однозначности функции могут быть получены произвольно точные результаты для обратной задачи. Однако в отрезке нарушения однозначности ошибка обучения (и ошибка обобщения) останется конечной, поскольку противоречие в данных, полученных из разных ветвей обратной функции, не устранимо. Значение ошибки обобщения пропорционально длине отрезка неоднозначности h. Такие задачи, корректное (единственное и устойчивое) решение которых может быть получено только для
некоторой подобласти множества значений, будем называть условно (или частично ) корректными9В книге [4.1], стр. 563, условно-корректными названы задачи, в постановку которых добавлено априорное предположение о существовании решения на некотором компакте. Для данного решения должна быть доказана теорема единственнности. В нашем рассмотрении в качестве такого компактного множества выступают отрезки, на которых обратная функция однозначна.
. -
Система C ( h=1 ). Прямая задача по-прежнему корректно поставлена, требуемое обучение и обобщение может быть достигнуто (
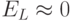 ). Однако ситуация качественно меняется для случая обратной задачи. Обратная функция двузначна на всем множестве значений, информация о ее значении минимальна. Обратная задача полностью некорректно поставлена.
). Однако ситуация качественно меняется для случая обратной задачи. Обратная функция двузначна на всем множестве значений, информация о ее значении минимальна. Обратная задача полностью некорректно поставлена.
Что общего между всеми этими примерами? В каждом из них ошибка обобщения при решении обратной задачи не может быть меньше значения, определяемого размером области неоднозначности h, который, таким образом, может рассматриваться, как мера некорректности задачи. В случае, если для решения обратной задачи используется метод со стабилизирующими свойствами (например, с малым числом свободных параметров по сравнению с числом обучающих примеров), будет получено гладкое решение с ненулевой ошибкой обучения, определяемой параметром h.
Заметим, что прямая задача является безусловно корректной только при полном отсутствии шума в обучающих данных. При наличии случайных компонент в значениях X имеется целое "облако" решений прямой задачи, причем размер облака пропорционален величине шума. Таким образом, нарушается единственность решения прямой задачи, и она становится некорректно поставленной.