Нейросетевые информационные модели сложных инженерных систем

Характер приближений в информационных моделях

Специфичность информационных моделей проявляется не только в способах их синтеза, но и характере делаемых приближений (и связанных с ними ошибок). Отличия в поведении системы и ее информационной модели возникают вследствие свойств экспериментальных данных.

• Информационные модели ab initio являются неполными. Пространства входных и выходных переменных не могут, в общем случае, содержать все параметры, существенные для описания поведения системы. Это связано как с техническими ограничениями, так и с ограниченностью наших представлений о моделируемой системе. Кроме того, при увеличении числа переменных ужесточаются требования на объем необходимых экспериментальных данных для построения модели (об этом см. ниже). Эффект опущенных (скрытых) входных параметров может нарушать однозначность моделируемой системной функции F.
• База экспериментальных данных, на которых основывается модель G рассматривается, как внешняя данность. При этом, в данных всегда присутствуют ошибки разной природы, шум, а также противоречия отдельных измерений друг другу. За исключением простых случаев, искажения в данных не могут быть устранены полностью.
• Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных задачи. Как следствие, получаемые модели будут обладать неодинаковой достоверностью и точностью в различных областях изменения параметров.
• Экспериментальные данные могут содержать пропущенные значения (например, вследствие потери информации, отказа измеряющих датчиков, невозможности проведения полного набора анализов и т.п.). Произвольность в интерпретации этих значений, опять-таки, ухудшает свойства модели.

Такие особенности в данных и в постановке задач требуют особого отношения к ошибкам информационных моделей.

Ошибка обучения и ошибка обобщения

Итак, при информационном подходе требуемая модель G системы F не может быть полностью основана на явных правилах и формальных законах. Процесс получения G из имеющихся отрывочных экспериментальных сведений о системе F может рассматриваться, как обучение модели G поведению F в соответствии с заданным критерием, настолько близко, насколько возможно. Алгоритмически, обучение означает подстройку внутренних параметров модели (весов синаптических связей в случае нейронной сети) с целью минимизации ошибки модели .

Прямое измерение указанной ошибки модели на практике не достижимо, поскольку системная функция F при произвольных значениях аргумента не известна. Однако возможно получение ее оценки:

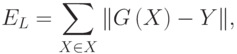
где суммирование по X проводится по некоторому конечному набору параметров X, называемому обучающим множеством. При использовании базы данных наблюдений за системой, для обучения может отводиться некоторая ее часть, называемая в этом случае обучающей выборкой. Для обучающих примеров X отклики системы Y известны^{7С учетом описанных выше особенностей экспериментальных данных.} . Норма невязки модельной функции G и системной функции Y на множестве X играет важную роль в информационном моделировании и называется ошибкой обучения модели.

Для случая точных измерений (например, в некоторых задачах классификации, когда отношение образца к классу не вызывает сомнений) однозначность системной функции для достаточно широкого класса G моделей гарантирует возможность достижения произвольно малого значения ошибки обучения E_L. Нарушение однозначности системной функции в присутствии экспериментальных ошибок и неполноты признаковых пространств приводит в общем случае к ненулевым ошибкам обучения. В этом случае предельная достижимая ошибка обучения может служить мерой корректности постановки задачи и качества класса моделей G.

В приложениях пользователя обычно интересуют предсказательные свойства модели. При этом главным является вопрос, каковым будет отклик системы на новое воздействие, пример которого отсутствует в базе данных наблюдений. Наиболее общий ответ на этот вопрос дает (по-прежнему недоступная) ошибка модели E. Неизвестная ошибка, допускаемая моделью G на данных, не использовавшихся при обучении, называется ошибкой обобщения модели E_G.

Основной целью при построении информационной модели является уменьшение именно ошибки обобщения, поскольку малая ошибка обучения гарантирует адекватность модели лишь в заранее выбранных точках (а в них значения отклика системы известны и без всякой модели!). Проводя аналогии с обучением в биологии, можно сказать, что малая ошибка обучения соответствует прямому запоминанию обучающей информации, а малая ошибка обобщения - формированию понятий и навыков, позволяющих распространить ограниченный опыт обучения на новые условия. Последнее значительно более ценно при проектировании нейросетевых систем, так как для непосредственного запоминания информации лучше приспособлены не нейронные устройства компьютерной памяти.

Важно отметить, что малость ошибки обучения не гарантирует малость ошибки обобщения. Классическим примером является построение модели функции (аппроксимация функции) по нескольким заданным точкам полиномом высокого порядка. Значения полинома (модели) при достаточно высокой его степени являются точными в обучающих точках, т.е. ошибка обучения равна нулю. Однако значения в промежуточных точках могут значительно отличаться от аппроксимируемой функции, следовательно ошибка обобщения такой модели может быть неприемлемо большой.

Поскольку истинное значение ошибки обобщения не доступно, в практике используется ее оценка. Для ее получения анализируется часть примеров из имеющейся базы данных, для которых известны отклики системы, но которые не использовались при обучении. Эта выборка примеров называется тестовой выборкой. Ошибка обобщения оценивается, как норма уклонения модели на множестве примеров из тестовой выборки.

Оценка ошибки обобщения является принципиальным моментом при построении информационной модели. На первый взгляд может показаться, что сознательное не использование части примеров при обучении может только ухудшить итоговую модель. Однако без этапа тестирования единственной оценкой качества модели будет лишь ошибка обучения, которая, как уже отмечалось, мало связана с предсказательными способностями модели. В профессиональных исследованиях могут использоваться несколько независимых тестовых выборок, этапы обучения и тестирования повторяются многократно с вариацией начального распределения весов нейросети, ее топологии и параметров обучения. Окончательный выбор "наилучшей" нейросети выполняется с учетом имеющегося объема и качества данных, специфики задачи, с целью минимизации риска большой ошибки обобщения при эксплуатации модели.