Математические методы в моделировании экономики
Цель лекции. Дать понятие экономико-математической модели и изложить основные этапы моделирования. Показать средства программы Mathcad для проведения наиболее распространенных математических преобразований в процессе решения математических моделей.
Принципы экономико-математического моделирования
Экономико-математическое моделирование - эффективный метод исследования сложных социально-экономических объектов и процессов. Практическими задачами моделирования являются анализ экономических объектов; экономическое прогнозирование, предвидение развития хозяйственных процессов и выработка управленческих решений. на всех уровнях.
Экономико-математическое моделирование основывается на принципе аналогии. Объект исследуется и изучается через рассмотрение другого, подобного ему и более доступного объекта, его модели. Модель создается исследователем с целью получения новых знаний об объекте-оригинале и отражает существенные (с точки зрения разработчика) свойства оригинала. Математическая модель – математический образ исследуемой системы, описывающий ее в абстрактной форме и адекватно отражающий структуру, свойства и взаимосвязи. Использование математических моделей позволяет осуществить предварительный выбор оптимальных или близких к ним вариантов решений по определенным критериям. Экономико-математическая модель - это математическая модель, предназначенная для исследования экономической проблемы. В ней отражаются основные соотношения между экономическими показателями.
Моделирование задачи включает следующие этапы:
- Определение проблемы. Четкая формулировка цели.
- Постановка задачи. Отбор объектов и ситуаций, реализующих поставленную цель, их качественный и количественный анализ.
- Системный анализ. Выдвигаются гипотезы. Сложные объекты, разбиваются на части (элементы), определяются связи элементов, свойства, выражаемые в виде уравнений, неравенств и т.п. Объект представляется в виде системы.
- Системный синтез. Математическая постановка задачи, в процессе которой осуществляется построение математической модели объекта и определение методов (алгоритмов) получения решения задачи. Как правило, подбирается известная математическая модель и алгоритм ее решения. Важно выбрать наиболее подходящий метод.
- Выбор программного обеспечения. Разработка программы.
- Решение и тестирование модели, анализ выходных данных. Если полученные результаты не удовлетворяют исследователя, то следует выбрать другую математическую модель; либо поставить задачу более корректно;
- Применение результатов исследований.
Экономико-математическое моделирование требует от исследователя четкости формулировки исследовательской задачи, строгой логичности в построении гипотез и концепций, умения пользоваться инструментарием высшей математики. В процессе построения и решения модели необходимо проводить аналитические математические преобразования в общем виде: исследование функций, дифференцирование и интегрирование, нахождение пределов, решение различного вида уравнений и систем уравнений. Символьный процессор программы Mathcad обеспечивает выполнение сложных математических операций простыми доступными средствами. Методика работы в Mathcad изложена в пособии "Mathcad 14: Основные сервисы и технологии". В этой лекции представлены аналитические методы решения распространенных математических задач в среде с Mathcad 14.
Математические операции в задачах экономико-математического моделирования
Рассмотрим ряд часто используемых математических операций, которые необходимы в процессе математического моделирования.
Дифференцирование
Для проведения операции дифференцирования в Mathcad надо ввести функцию под знак  . (панель Calculus), щелкнуть оператор символьного вывода (панель Symbolic или Evaluation). В программе можно находить частные производные, производные второго, третьего, высоких порядков.
. (панель Calculus), щелкнуть оператор символьного вывода (панель Symbolic или Evaluation). В программе можно находить частные производные, производные второго, третьего, высоких порядков.
Дифференциальное исчисление часто применяется в процессе экономического анализа. При построении модели, анализе экономических показателей возникают вопросы: от каких факторов зависят показатели, каковы их оптимальные значения, какова степень зависимости. Задачи на нахождение экстремума, анализ системы на устойчивость, исследование взаимосвязи экономических показателей, скорости изменения решаются с использованием дифференциального исчисления.
Пример 1.1.
Рассмотрим пример исследования эластичности. Коэффициент эластичности  показывает относительное изменение исследуемого экономического показателя Y под действием единичного относительного изменения экономического фактора x, от которого зависит показатель. Функция имеет вид:
показывает относительное изменение исследуемого экономического показателя Y под действием единичного относительного изменения экономического фактора x, от которого зависит показатель. Функция имеет вид:
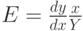 |
( 1.1) |
где 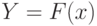 . В зависимости от вида функции эластичность по-разному зависит от фактора
. В зависимости от вида функции эластичность по-разному зависит от фактора  .
.
Пусть зависимость экономического показателя  от фактора
от фактора  описывается функцией:
описывается функцией:
- показательной
- обратной
 ,
, - линейной
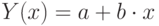 .
.
Определить вид зависимости коэффициента эластичности.
Решение показано на рисунке 1.1.
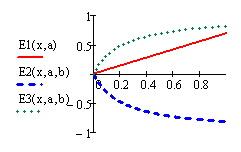
Рис. 1.1. Листинг решения Примера 1.1. Расчет эластичности для разных функций зависимости экономического показателя от заданного фактора
 - коэффициент эластичности
- коэффициент эластичности 
 и
и  - параметры
- параметры
-
Показательная функция:

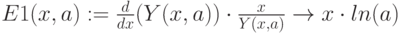
-
Обратная функция:


-
Линейная функция:


