Имитационное моделирование
Цель лекции. Научить строить модель задачи, в которой ключевые данные не могут быть точно определены. Показать, как выделить стохастические переменные, выбрать и построить для них закон распределения. Показать применение функций Mathcad для реализации метода Монте-Карло. Представить, как провести анализ результата.
5.1 Постановка задач имитационного моделирования
В первой главе описаны основные этапы экономико-математического моделирования. После того, как математическая модель построена, выбирается программное обеспечение для ее реализации на компьютере, производится разработка и расчет компьютерной модели. Использование компьютеров дает возможность представить сложный экономический процесс посредством искусственных процессов-аналогов, которые можно реализовать на ЭВМ, и выполнить оптимизацию исследуемых параметров в режиме "имитации". Имитация - это компьютерный эксперимент, который проводится с моделью системы, а не с самой системой. Для этого выбираются специальные имитирующие компьютерные программы и технологии программирования. В процессе машинного эксперимента меняют те или иные показатели, т.е. изменяют состояние объекта и регистрируют его поведение в новых условиях. Математическую динамическую модель называют имитационной моделью. Имитационной моделью называют также специальный программный комплекс, который позволяет имитировать деятельность какого-либо сложного объекта [23, 24].
В этой главе рассмотрим задачи, в которых свойства изучаемого объекта точно не определены. Переменные модели - стохастические, их значения не могут быть точно установлены или предсказаны. Неопределенность стохастических переменных связана с недостаточностью информации о них. Неопределенность вероятностных переменных связана с вероятностным характером описываемых ими процессов. Не зная точных исходных данных, используя компьютерные технологии, мы имеем возможность непрерывно и случайным образом генерировать значения исходных величин и затем рассчитывать значения выходной переменной. Для оценки характеристик исследуемых совокупностей используется аппарат теории вероятности, теории случайных функций, понятие случайной величины [25].
Если входные переменные являются стохастическими, то и выходные зависимые переменные также будут стохастическими. При моделировании систем, содержащих вероятностные элементы, используются методы Монте-Карло [24, 26]. Это общее название группы методов решения задач, в которых реализуется построение вероятностных распределений возможных значений выходной стохастической переменной при изменении входных переменных, которые генерируются в виде случайных последовательностей. Стохастические переменные моделируются как случайные величины с определенным законом распределения вероятностей. При численном решении задач, включающих стохастические переменные, используется метод статистических испытаний, который заключается в моделировании случайных величин. На практике эти величины получают путем некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Экономические показатели (цены, прибыль, затраты и т.д) моделируются как случайные числа с каким-либо распределением. Повторяющиеся испытания реализуются путем генерации случайных совокупностей этих параметров. Статистические результаты получаются в результате обработки этих совокупностей. Вероятность того, что результаты отличаются от истинных не более чем на заданную величину, есть функция количества испытаний или размера сгенерированных выборок. Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел. Для исследователя представляют интерес выводы, носящие характер статистических показателей, представленных в виде графиков или таблиц, в которых каждому варианту исследуемых параметров поставлены в соответствие определенные средние значения с набором характеристик их распределения.
5.2 Основные этапы имитационного моделирования
В общем случае проведение имитационного моделирования происходит по общепринятой схеме, но поскольку переменные модели являются стохастическими, надо проводить анализ этих переменных. Для моделирования стохастических переменных, используются компьютерные технологии, с помощью которых случайным образом генерируются значения исходных величин и затем рассчитываются значения выходной переменной. Для оценки характеристик исследуемых совокупностей 
и 
используется аппарат теории вероятности и теории случайных функций. Приведем основные этапы имитационного моделирования.
Прежде всего, надо четко определить цель моделирования. Когда цель определена, выделяются следующие этапы:
- Выбрать основные объекты и величины, описывающие исследуемый процесс. Определить входные показатели
.. - Выбрать и рассчитать выходные показатели, описывающие модель системы. Для этого выбрать закон изменения переменных, описывающий исследуемый процесс, - функциональную зависимость
. Тогда математическая модель системы или процесса имеет вид: 
( 5.1) - Задать числовые значения показателей, задать граничные условия - установить взаимосвязи между различными показателями в виде математических уравнений или неравенств
- Задать законы распределения вероятностей для ключевых параметров модели. В зависимости от информации о данных выбрать законы распределения случайных величин. Исходя из условий задачи, можно выбрать несколько альтернативных вариантов, рассмотреть их и сравнить полученные решения.
- Провести компьютерную имитацию значений ключевых параметров модели. Провести генерацию случайных значений. Для этого предварительно выбрать программное обеспечение, с использованием которого будет решаться задача.
- Рассчитать основные характеристики вероятностных распределений выходных показателей. С использованием выбранной программы провести статистический анализ полученных случайных совокупностей.
- Провести анализ полученных результатов и принять решение. На основании статистического анализа проделать экономический анализ полученных результатов.
Результаты имитационного эксперимента могут использоваться для построения прогнозных моделей и сценариев. Рассмотрим реализацию метода Монте –Карло в программе Mathcad.
5.3 Имитационное моделирование прибыли фирмы методом Монте-Карло
Рассмотрим технику имитационного моделирования методом Монте-Карло на примере исследования прибыли фирмы. Рассмотрим, например, рекламную деятельность фирмы.
Задача 5.1.
Фирма предполагает инвестировать сумму 2 млн. руб., используя денежные средства от рекламной деятельности. Предоставляются рекламные услуги по заказам клиентов. Количество и стоимость заказов - величины постоянно меняющиеся. Затраты составляют в среднем 20% от стоимости заказов. Необходимо оценить, какую прибыль может получить фирма за год в таких условиях, насколько она отличается от 2 млн. руб.
Постановка задачи
Цель задачи – рассчитать прибыль за год и оценить риск быть меньше 2 млн. руб. Разделим переменные на стохастические и постоянные и определим возможные границы их изменений. Стохастические переменные моделируем в виде случайных совокупностей с определенным законом распределения вероятностей. Выходной показатель – прибыль представляем в виде статистических показателей, гистограммы распределения, графиков.
Модель задачи
Определим основные параметры, описывающие задачу, введем обозначения:
Стохастические переменные:
-
- процент изменения количества заказов. -
- количество заказов в месяц, -
- стоимость заказа,
Постоянные параметры:
-
процент затрат постоянный в течение всего года.
Проведен анализ по оценке деятельности фирмы за прошедший год, и на его основе сделаны предположения о численных значениях параметров в месяц (таблица 5.1) .
| Показатели (значения в месяц) | Вероятное значение | Пределы изменения | |
|---|---|---|---|
| Изменяемые | Количество заказов Q | 120 | |
| Ежемесячный процент изменения числа заказов dQ | От -5% до 8% | ||
| Стоимость заказа P(руб.) | 1800 | От 1400 до 2000 | |
| Постоянные. | Процент затрат F% от стоимости заказа | 20% |
По оценкам стоимость заказа будет меняться в пределах от 1000 до 2000 руб, с вероятным значением 1800 руб. Количество заказов будет определяться как сумма количества заказов 
в предшествующем месяце и его изменения , которое флуктуирует между 5% уменьшения и 8% увеличения. Для расчета принимается среднее количество заказов в месяц за пошедший год 
. Тогда имеем
 |
( 5.1) |
Выходные показатели. Прибыль фирмы 
за год - сумма месячных прибылей с учетом процента затрат. Прибыль за месяц 
- стохастическая переменная определяется как произведение случайных величин количества заказов в месяц и стоимости заказа 
.
 |
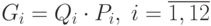( 5.2) |
 |
( 5.2) |
Выбор законов распределения вероятностей стохастических переменных.
Необходимо учесть вероятностный характер моделируемого показателя. Аппроксимируем и 
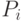случайными числами с каким-либо законом вероятности. Выбор законов распределения вероятностей исходных данных определяет сценарии развития ситуаций – различные варианты решения задачи. Рассмотрим следующий вариант распределения ключевых переменных: изменение количества заказов в течение – равномерное распределение, стоимость заказа - нормальное распределение.
Компьютерная имитация ключевых параметров модели. Для генерации случайных совокупностей используем средства Mathcad. Для генерации случайных величин с заданным распределением существуют функции из категории Random numbers .
Анализ полученных результатов. Статистический анализ результатов сделаем, используя статистические функции Mathcad из категории Statistics. Все полученные результаты проанализируем, делая численные оценки прибыли и построим наилучший и наихудший сценарий.