Нейронные сети ассоциативной памяти
Нейронные сети ассоциативной памяти
Вычислительный центр СО РАН в г. Красноярске
Рассматриваются нейронные сети ассоциативной памяти, восстанавливающие по искаженному и/или зашумленному образу ближайший к нему эталонный. Исследована информационная емкость сетей и предложено несколько путей ее повышения, в том числе - ортогональные тензорные (многочастичные) сети. Построены способы предобработки, позволяющие конструировать нейронные сети ассоциативной памяти для обработки образов, инвариантной относительно групп преобразований. Описан численный эксперимент по использованию нейронных сетей для декодирования различных кодов.
Введение
Прежде чем заниматься конструированием сетей ассоциативной памяти необходимо ответить на следующие два вопроса: "Как устроена ассоциативная память?" и "Какие задачи она решает?". Когда мы задаем эти вопросы, имеется в виду не устройство отделов мозга, отвечающих за ассоциативную память, а наше представление о макропроцессах, происходящих при проявлении ассоциативной памяти.
Принято говорить, что у человека возникла ассоциация, если при получении некоторой неполной информации он может подробно описать объект, к которому по его мнению относится эта информация. Достаточно хорошим примером может служить описание малознакомого человека. К примеру, при высказывании: "Слушай, а что за парень, с которым ты вчера разговаривал на вечеринке, такой высокий блондин?"- у собеседника возникает образ вчерашнего собеседника, не ограничивающийся ростом и цветом волос. В ответ на заданный вопрос он может рассказать об этом человеке довольно много. При этом следует заметить, что содержащейся в вопросе информации явно недостаточно для точной идентификации собеседника. Более того, если вчерашний собеседник был случайным, то без дополнительной информации его и не вспомнят.
В качестве другого примера можно рассмотреть ситуацию, когда ваша однокурсница появляется в институте с совершенно новой прической и в незнакомой вам одежде. При этом вы, тем не менее, чаще всего ее узнаете и сможете определить чем ее новый образ отличается от привычного. Можно предположить, что это происходит следующим образом. При виде ее нового облика в вашей памяти возникает ассоциация с привычным для вас. А далее сравнивая эти два облика вы можете определить отличия.
Исходя из рассмотренных примеров можно сказать, что ассоциативная память позволяет по неполной и даже частично недостоверной информации восстановить достаточно полное описание знакомого объекта. Слово знакомого является очень важным, поскольку невозможно вызвать ассоциации с незнакомыми объектами. При этом объект должен быть знаком тому, у кого возникают ассоциации.
Одновременно рассмотренные примеры позволяют сформулировать решаемые ассоциативной памятью задачи:
- Соотнести входную информацию со знакомыми объектами, и дополнить ее до точного описания объекта.
- Отфильтровать из входной информации недостоверную, а на основании оставшейся решить первую задачу.
Очевидно, что под точным описанием объекта следует понимать всю информацию, которая доступна ассоциативной памяти. Вторая задача решается не поэтапно, а одновременно происходит соотнесение полученной информации с известными образцами и отсев недостоверной информации.
Постановка задачи
Пусть задан набор из  эталонов -
эталонов -  -мерных векторов
-мерных векторов  . Требуется построить сеть, которая при предъявлении на вход произвольного образа - вектора x - давала бы на выходе "наиболее похожий" эталон.
. Требуется построить сеть, которая при предъявлении на вход произвольного образа - вектора x - давала бы на выходе "наиболее похожий" эталон.
Всюду далее образы и, в том числе, эталоны -  -мерные векторы с координатами
-мерные векторы с координатами  . Эталон, "наиболее похожий" на x - ближайший к x вектор
. Эталон, "наиболее похожий" на x - ближайший к x вектор 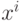 . Легко заметить, что это требование эквивалентно требованию максимальности скалярного произведения векторов
. Легко заметить, что это требование эквивалентно требованию максимальности скалярного произведения векторов  и
и  :
:
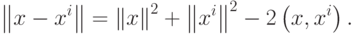
Первые два слагаемых в правой части совпадают для любых образов  и
и 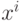 , так как длины всех векторов-образов равны
, так как длины всех векторов-образов равны  . Таким образом, задача поиска ближайшего образа сводится к поиску образа, скалярное произведение с которым максимально. Этот простой факт приводит к тому, что сравнивать придется линейные функции от образов, тогда как расстояние является квадратичной функцией.
. Таким образом, задача поиска ближайшего образа сводится к поиску образа, скалярное произведение с которым максимально. Этот простой факт приводит к тому, что сравнивать придется линейные функции от образов, тогда как расстояние является квадратичной функцией.
