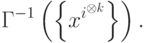НОУ ИНТУИТ | Нейроинформатика. Лекция 8: Нейронные сети ассоциативной памяти

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Доступ: свободный | Студентов: 1638 / 246 | Оценка: 4.58 / 4.39 | Длительность: 20:15:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист

|

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Тензорные сети

Для увеличения числа линейно независимых эталонов, не приводящих к прозрачности сети, используется прием перехода к тензорным или многочастичным сетям [8.3, 8.4, 8.5, 8.6, 8.7].

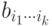Тензорным произведением -мерных векторов $y^1 , \cdots ,y^k$ называется -индексная величина $b_{i_1 \cdots i_k }$ , у которой все индексы независимо пробегают весь набор значений от единицы до , а $b_{i_1 \cdots i_k } = y_{i_1 }^1 y_{i_2 }^2 \cdots y_{i_k }^k$ . -ой тензорной степенью вектора будем называть вектор $x^{ \otimes k}$ , полученный как тензорное произведение векторов . Вектор $x^{ \otimes k}$ является n^k -мерным вектором. Однако пространство $L\left( {\left\{ {x^{i^{ \otimes k}}} \right\}} \right)$ имеет размерность, не превышающую величину $r_{n,k} = \sum\limits_{i = 0}^k {{\bf{C}}_{n - 1}^i }$ , где ${\bf{C}}_p^q = \frac{{p!}}{{q!\left( {p - q} \right)!}}$ - число сочетаний из по .

Теорема. При k < n в ранг $r_{n,k}$ множества $\left\{ {x^{ \otimes k} } \right\}$ равен: $r_{n,k} = \sum\limits_{i = 0}^k {{\bf{C}}_{n - 1}^i }$ .

Рис. 8.2. "Тензорный" треугольник Паскаля

Небольшая модернизация треугольника Паскаля, позволяет легко вычислять эту величину. На рис. 8.2 приведен "тензорный" треугольник Паскаля. При его построении использованы следующие правила:

Первая строка содержит двойку, поскольку при n=2 в множестве X всего два неколлинеарных вектора.
При переходе к новой строке, первый элемент получается добавлением единицы к первому элементу предыдущей строки, второй - как сумма первого и второго элементов предыдущей строки, третий - как сумма второго и третьего элементов и т.д. Последний элемент получается удвоением последнего элемента предыдущей строки.

Таблица 8.1.
n	k	n^k	C^{k - 1}_{n + k - 1}	r_n,k
5	2	25	15	11
	3	125	35	15
10	3	1 000	220	130
	6	1 000 000	5005	466
	8	100 000 000	24310	511

В таблица 8.1 приведено сравнение трех оценок информационной емкости тензорных сетей для некоторых значений n и k. Первая оценка - n^k - заведомо завышена, вторая - ${\bf{C}}_{n + k - 1}^{k - 1}$ - дается формулой Эйлера для размерности пространства симметричных тензоров и третья - точное значение $r_{n,k}$

Как легко видеть из таблицы таблица 8.1, уточнение при переходе к оценке $r_{nk}$ является весьма существенным. С другой стороны, предельная информационная емкость тензорной сети (число правильно воспроизводимых образов) может существенно превышать число нейронов, например, для 10 нейронов тензорная сеть валентности 8 имеет предельную информационную емкость 511.

Легко показать, что если множество векторов $\left\{ {x^i } \right\}$ не содержит взаимно обратных, то размерность пространства $L\left( {\left\{ {x^{i^{ \otimes n}} } \right\}} \right)$ равна числу векторов в множестве $\left\{ {x^i } \right\}$ . Сеть (2) для случая тензорных сетей имеет вид

$x' = Sign\left( {\sum\limits_{i = 1}^m {\left( {x^{ \otimes k} ,x^{i^{ \otimes k}} } \right)x^i } } \right) = Sign\left( {\sum\limits_{i = 1}^m {\left( {x,x^i } \right)^k x^i } } \right) ,$

( 9)

а ортогональная тензорная сеть

$x' = Sign\left( {\sum\limits_{i = 1}^m {\left( {x^{ \otimes k} ,v^i } \right)x^i } } \right) = Sign\left( {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {\gamma_{ij}^{ - 1} } \left( {x,x^j } \right)^k x^i } } \right) ,$

( 10)

где $\gamma_{ij}^{-1}$ - элемент матрицы

$\Gamma^{ - 1} \left( {\left\{ {x^{i^{ \otimes k}} } \right\}} \right).$

Сеть (9) хорошо работает на слабо скоррелированных эталонах, а сеть (10) не чувствительна к степени скоррелированности эталонов.

Дальше >>

Авторизоваться

Нейроинформатика

Нейронные сети ассоциативной памяти

Тензорные сети

Вопросы и ответы