|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Принципы квантовых вычислений
Квантовые алгоритмы и квантовые вычисления, их преимущества
Как и в классических вычислениях, обработку информации путем применения квантовых логических операций можно описывать по-разному:
- как выполнение в определенной последовательности элементарных преобразований, т.е. как последовательное применение к имеющимся данным (операндам) ряда операторов, – в этом случае говорят о квантовых программах или алгоритмах;
- как последовательную обработку потока данных в сети квантовых логических вентилей или "гейтов" (от англ. gate), – тогда говорят о квантовых схемах.
Оба эти подхода, как и в классической вычислительной технике, с точки зрения конечного результата обработки информации являются эквивалентными.
Доказано, что из квантовых вентилей можно построить квантовые логические схемы для вычисления любой классической функции. Считается, что для квантовых вычислений имеет силу даже "усиленный" тезис Черча–Тьюринга–Дойча, а именно: с помощью квантовых логических схем (квантовых алгоритмов) можно смоделировать любой физический процесс, ограниченный в пространстве и времени.
Обоснован ряд функционально полных наборов квантовых логических операций (вентилей).
В 1997 г. была детально разработана одна из возможных теоретических моделей универсальной квантовой машины Тьюринга [Bernstein E., Vazirani U.V. Quantum complexity theory. // Society for Industrial and APPLIED Mathematics Journal on Computing. – 1997. – v. 26, No. 5. – P. 1411-1473].
Однако серьезное внимание научного сообщества к квантовым вычислениям было привлечено лишь тогда, когда были предложены алгоритмы квантовых вычислений для задач, непосильных для мощнейших классических ЭВМ.
Первым из них был квантовый алгоритм факторизации, т.е. разложения многозначных целых чисел на простые множители, предложенный в 1994 г. П. Шором. Наиболее эффективный из известных классических алгоритмов факторизации требует для решения этой задачи количество вычислительных операций порядка ![exp(a\sqrt[3]{n})](/sites/default/files/tex_cache/d740b5325520285d6414173f4bdb7935.png) , где
, где  – константа,
– константа,  – количество десятичных знаков в разлагаемом на множители числе. Уже при
– количество десятичных знаков в разлагаемом на множители числе. Уже при 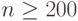 задача не может быть решена за разумное время даже на мощнейших многопроцессорных современных суперкомпьютерах.
На этом факте основан, кстати, популярнейший ныне криптографический протокол RSA, обеспечивающий надежную защиту важной информации от посторонних лиц. Квантовый алгоритм П. Шора требует для решения этой задачи количество квантовых вычислительных операций, которое не экспоненциально, а только полиномиально зависит от
задача не может быть решена за разумное время даже на мощнейших многопроцессорных современных суперкомпьютерах.
На этом факте основан, кстати, популярнейший ныне криптографический протокол RSA, обеспечивающий надежную защиту важной информации от посторонних лиц. Квантовый алгоритм П. Шора требует для решения этой задачи количество квантовых вычислительных операций, которое не экспоненциально, а только полиномиально зависит от  . Поэтому квантовый компьютер, в состав которого входят порядка 1000 кубитов, с тактовой частотой порядка 1 ГГц был бы способен управиться с факторизацией целых чисел длиной 200 десятичных знаков уже за несколько минут!
. Поэтому квантовый компьютер, в состав которого входят порядка 1000 кубитов, с тактовой частотой порядка 1 ГГц был бы способен управиться с факторизацией целых чисел длиной 200 десятичных знаков уже за несколько минут!
Алгоритм П. Шора стал настоящим открытием для вычислительной математики. Ведь оказалось, что классы сложности задач для классических и для квантовых вычислений не совпадают, что квантовые вычисления некоторых важных типов задач могут быть намного более эффективными, чем классические.
Это подтвердил и опубликованный Л. Гровером в 1996 г. алгоритм быстрого поиска в неструктурированной базе данных. В то время как классический поиск нужной записи требует в среднем  операций, где
операций, где  – общее число записей, предложенный Л. Гровером квантовый алгоритм позволяет найти нужную запись приблизительно за
– общее число записей, предложенный Л. Гровером квантовый алгоритм позволяет найти нужную запись приблизительно за  квантовых операций.
квантовых операций.
Эффективность алгоритмов П. Шора и Л. Гровера основана на использовании существенных преимуществ сплетенных состояний и экспоненциально возрастающего квантового параллелизма обработки информации в таких состояниях.
С тех пор разработано уже немало эффективных квантовых алгоритмов для решения таких практически важных задач, как быстрые квантовые преобразования Фурье, выявление периодичности очень сложных функций и нахождение их периодов, распознавание структур абстрактной алгебры и их функций, проверка тождественности очень сложных формул логики предикатов, вычисление и преобразование числовых матриц больших размеров, нахождение собственных значений и собственных векторов матричных операторов, решение многомерных задач дискретной оптимизации и т.п.
Квантовые вычисления значительно эффективнее, чем классические, при моделировании поведения многокомпонентных квантовых систем, – сложных молекул, химических радикалов, взаимодействий между ними, атомных ядер, других ансамблей из многих элементарных частиц, биологических мембран и т.п.
И в результате стало очевидным то, что работать над практической реализацией квантовых вычислений несомненно следует. Поэтому конец ХХ – начало ХХІ в. ознаменовались значительной активизацией исследований и разработок квантовых алгоритмов, подходов к программированию квантовых вычислений, а также путей реализации кубитов и квантовых схем.
Декогерентизация и квантовая коррекция ошибок
Эксперименты уже с первыми действующими образцами квантовых процессоров из небольшого числа кубитов выявили тот досадный факт, что отдельные кубиты и тем более группы кубитов не удается долго удерживать в "когерентном" состоянии, когда сохраняются постоянными разности фаз между волновыми функциями. Дело в том, что ни отдельный кубит, ни квантовый регистр в целом на самом деле никогда не являются полностью изолированными от окружающей среды системами. Как ни стараются экспериментаторы, им не удается полностью исключить влияние хаотического теплового движения частиц, внешних случайных электромагнитных полей, внешнего гравитационного поля, космических потоков нейтрино и других частиц, шумов физического вакуума и т.д.
Квантовые логические операции тоже не выполняются абсолютно точно. Действуя нацелено на один, на два или на группу кубитов, не удается полностью устранить нежелательное, пусть и совсем незначительное, частичное влияние на соседние кубиты. Если обратиться к
рис.
8.1, то влияние всех этих посторонних шумовых факторов наглядно можно представить как хаотические отклонения ("дрейф") вектора состояния кубита под действием посторонних влияний от своего "идеального" положения  .
.
Более того, когда кубит находится в связи со своим окружением, его состояние, строго говоря, описывается уже т.н. "матрицей плотности". В данном случае речь идет о плотности вероятности различных состояний системы "кубит – окружение". Вектор состояния кубита может иметь длину уже меньше единицы, т.е. его острие находится не обязательно на поверхности, а может располагаться и внутри сферы Блоха. Чем больше энергия взаимодействия кубита с окружением относительно его внутренней энергии, тем больше могут быть эти отклонения.
За продолжительное время вектор состояния может неконтролируемо "дрейфовать" довольно далеко. А это изменяет связь его фазы с фазами других кубитов. Имеет место постепенная потеря когерентности. А время от времени совпадение нескольких внешних влияний действует как процесс считывания: кубит скачком переходит в одно из своих базовых состояний. В случае взаимодействия ряда кубитов, особенно в сплетенных состояниях, это приводит к непредвиденному изменению состояния всего квантового регистра. И чем больше кубитов в регистре, тем чаще имеет место потеря когерентности. Это явление называют "декогерентизацией" (от англ. "decoherence"). Из-за этого в квантовых вычислениях происходят ошибки, и дальше эволюция квантового процессора становится уже неконтролируемой.
Чтобы легче понять, что такое декогерентизация, снова взгляните на рис. 8.2 и вообразите себе, что под одним из поплавков промелькнула рыбка или на него случайно упал листочек, в результате чего фаза его колебаний, а может и частота, немного сбились. Ясно, что результат интерференции волн изменится, а поскольку все поплавки сплетены, то это немного повлияет и на колебания других поплавков.
К счастью, однако, оказалось, что с разрушительным влиянием декогерентизации можно успешно бороться с помощью хорошо продуманных методов кодирования, периодического контроля, своевременного выявления и квантовой коррекции ошибок.
Методы выявления и коррекции сбоев и ошибок были хорошо разработаны уже в классической вычислительной технике, где на практике доказана высокая эффективность "избыточного" кодирования, когда п бит данных специальными способами кодируются ( )-битным кодом. Это позволяет эффективно обнаруживать одно-, двух- и даже многобитовые ошибки и корректировать их. Подобная идея используется и в квантовом случае. Правда, квантовая коррекция ошибок оказалась намного более сложной, ведь речь идет не о битах, а о кубитах, – вместе со всеми их особенностями. Дополнительно затрудняет дело невозможность "клонирования", т.е. создания нескольких копий состояния кубитов.
)-битным кодом. Это позволяет эффективно обнаруживать одно-, двух- и даже многобитовые ошибки и корректировать их. Подобная идея используется и в квантовом случае. Правда, квантовая коррекция ошибок оказалась намного более сложной, ведь речь идет не о битах, а о кубитах, – вместе со всеми их особенностями. Дополнительно затрудняет дело невозможность "клонирования", т.е. создания нескольких копий состояния кубитов.
Имеются, однако, и специфически квантовые преимущества. Например, уже в случае одного кубита можно считать допустимыми не все его квантовые состояния. Сферу Блоха ( рис. 8.1) можно разбить на отдельные участки, например, аппроксимируя ее правильным многогранником, и считать допустимыми лишь квантовые состояния, которые представлены векторами, проведенными к центру граней. Если из-за внешних влияний вектор состояния сместится за некоторое время (период контроля) из своего допустимого положения, но останется в пределах грани, то при периодическом контроле он может быть принудительно возвращен в центр грани, что позволяет поддерживать допустимое состояние кубита неизменным как угодно долго.
Эффективные методы кодирования, диагностики отклонений и их квантовой коррекции уже найдены и детально разработаны. Мы не станем здесь их объяснять, так как это – задача другого курса лекций. Укажем лишь, что найденные методы позволяют поддерживать контролируемый процесс квантовых вычислений как угодно долго, если вероятность ошибки при выполнении одной квантовой логической операции ниже определенного уровня – порядка одной ошибки на 104–105 квантовых операций.
Программа периодического контроля, выявления, диагностики и квантовой коррекции ошибок должна запускаться в начале квантовых вычислений и работать в фоновом режиме. Из-за необходимости избыточного кодирования значительно (иногда в несколько раз) возрастает и суммарное количество требуемых для квантовых вычислений кубитов. Но благодаря этому квантовые вычисления становятся практически возможными даже при наличии декогерентизации.
Технические требования к элементной базе квантового процессора
Функциональная схема электронного комплекса для квантовых вычислений, как это представляется сегодня, изображена на рис. 8.4.
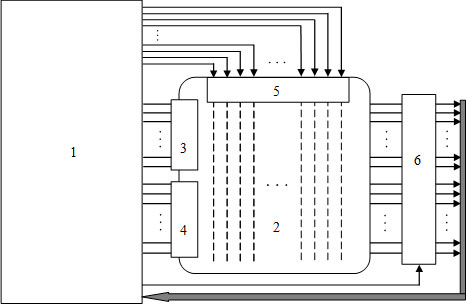
Рис. 8.4. Функциональная схема аппаратуры для квантовых вычислений: 1 – классическая быстродействующая ЭВМ; 2 – квантовый процессор; 3, 4 – устройства записи информации в квантовые регистры; 5 – устройство управления квантовыми операциями; 6 – устройство считывания информации с кубитов
Цикл работы комплекса начинается с "инициализации" – занесения в первую часть квантового регистра через устройство 3 нужного набора начальных данных. Соответствующие кубиты переводятся при этом в заведомо заданные базовые квантовые состояния. Через устройство 4 все другие кубиты переводятся в базовое квантовое состояние "0". Дальше с помощью устройства 5 сначала выполняется преобразование Уолша-Адамара, вследствие чего квантовый регистр переходит в одно из максимально сплетенных состояний. А потом выполняется ряд предусмотренных программой квантовых операций, в ходе которых происходят целенаправленные взаимосогласованные преобразования одновременно миллиардов и миллиардов миллиардов комплексных амплитуд. Достигается такая степень параллелизма, которая "и не снилась" классическим компьютерам.
Когда преобразования заканчиваются, с помощью устройства 6 информация считывается с кубитов и передается в классический компьютер. Программой работы может быть предусмотрено также промежуточное считывание состояния лишь нескольких или даже одного из всех кубитов. По результатам промежуточного считывания выбирается одно из многих возможных продолжений программы, и цикл повторяется.
Предполагается и многоразовое повторение одной программы при разных вариантах начальных данных. Такого рода комплекс обеспечивает эффективное объединение преимуществ как классических, так и квантовых вычислений.
Элементная база практически полезного квантового процессора должна удовлетворять следующим техническим требованиям:
- процессор должен составляться не менее чем из примерно 1000 слабо взаимодействующих кубитов, поскольку лишь в этом случае экономически оправдываются затраты на его реализацию по сравнению с современными классическими суперкомпьютерами;
- должна быть обеспечена возможность надежной записи информации, если не в каждый, то в значительное число кубитов, и промежуточного считывания состояния некоторых кубитов, а также считывание конечного результата из всей выходной части квантового регистра;
- квантовый процессор должен быть настолько хорошо изолирован от внешних влияний, определяющих его декогерентизацию, чтобы гарантированное время сохранения когерентности было достаточным для выполнения по крайней мере 104–105 квантовых логических операций;
- в процессоре должна быть обеспечена возможность контролируемого выполнения функционально полного набора квантовых логических операций;
- эффективное избыточное кодирование и фоновые программы диагностики и квантовой коррекции ошибок должны поддерживать процесс квантовых вычислений достаточно долго;
- в состав процессора должны входить достаточно быстрые и надежные шины связи;
- в процессоре должна иметься оперативная память для хранения и повторного использования промежуточных результатов вычислений.
