|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Принципы квантовых вычислений
Введение
Конец ХХ и начало ХХІ века ознаменовались значительной активизацией исследований и разработок в области квантовых вычислений.
Если в ХХ в. дальнейший прогресс вычислительной техники связывали в основном с усовершенствованием микроэлектронной и с переходом к наноэлектронной элементной базе информатики, с повышением степени интеграции и быстродействия интегральных схем, с использованием параллельной и аналоговой обработки изображений, со специализацией и наращиванием количества параллельно работающих процессоров, то сейчас большие надежды стали возлагаться также на кардинально новую квантовую элементную базу, на квантовую информатику и квантовые вычисления. С основными принципами, лежащими в основе таких вычислений, мы и ознакомим вас в данной лекции.
Основные положения квантовой механики, важные для квантовых вычислений
Напомним известные положения квантовой механики, важные для понимания особенностей квантовой информатики.
Физическое состояние и поведение квантовых объектов описываются комплексной функцией  , которую называют "волновой" и аргументы которой
, которую называют "волновой" и аргументы которой  выбирают в зависимости от того, с какой стороны, с какой точки зрения рассматривается квантовый объект. Если нас интересует, например, пространственное расположение электронов вокруг ядра атома или в молекуле, то аргументами волновой функции будут пространственные координаты электронов
выбирают в зависимости от того, с какой стороны, с какой точки зрения рассматривается квантовый объект. Если нас интересует, например, пространственное расположение электронов вокруг ядра атома или в молекуле, то аргументами волновой функции будут пространственные координаты электронов  относительно центра массы. Волновая функция в этом случае описывает пространственную структуру электронной "шубы" атома или молекулы – своего рода "стоячую волну" вокруг ядра или нескольких ядер. Соответствующие примеры мы уже рассматривали в предыдущих разделах. Вспомните, например, атомные и молекулярные орбитали.
относительно центра массы. Волновая функция в этом случае описывает пространственную структуру электронной "шубы" атома или молекулы – своего рода "стоячую волну" вокруг ядра или нескольких ядер. Соответствующие примеры мы уже рассматривали в предыдущих разделах. Вспомните, например, атомные и молекулярные орбитали.
Волновая функция "нормируется" так, чтобы интеграл от квадрата ее модуля по всему пространству равнялся единице:
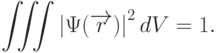 |
( 8.1) |
При этом величину  можно трактовать как "плотность электронной шубы" в точке
можно трактовать как "плотность электронной шубы" в точке  пространства или как плотность вероятности того, что электрон находится внутри элемента пространства
пространства или как плотность вероятности того, что электрон находится внутри элемента пространства  с координатами
с координатами  .
.
Если же нас интересует, скажем, динамическое поведение квантового объекта во внешнем магнитном поле, то аргументами волновой функции являются время  и вектор
и вектор  магнитного момента этого объекта, в частности его проекция на направление силовых линий поля. А волновая функция описывает в этом случае особенности состояний равновесия и прецессии квантового объекта в магнитном поле. Она тоже нормируется так, чтобы интеграл от квадрата ее модуля по всем возможным направлениям в любой момент времени равнялся единице. Тогда
магнитного момента этого объекта, в частности его проекция на направление силовых линий поля. А волновая функция описывает в этом случае особенности состояний равновесия и прецессии квантового объекта в магнитном поле. Она тоже нормируется так, чтобы интеграл от квадрата ее модуля по всем возможным направлениям в любой момент времени равнялся единице. Тогда  можно рассматривать как плотность вероятности соответствующей ориентации магнитного момента объекта или как плотность распределения многих идентичных квантовых объектов по ориентации их в магнитном поле в момент времени
можно рассматривать как плотность вероятности соответствующей ориентации магнитного момента объекта или как плотность распределения многих идентичных квантовых объектов по ориентации их в магнитном поле в момент времени  .
.
Рассмотрение волновой функции как комплексной функции разных наборов аргументов называют разными "представлениями" квантового объекта, которые, как правило, не являются альтернативными, а, наоборот, существенно дополняют друг друга.
Если силовое поле квантового объекта не зависит от времени (другими словами – является стационарным), то волновая функция этого объекта может быть записана в виде
 |
( 8.2) |
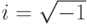 – мнимая единица,
– мнимая единица, 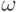 – круговая частота собственных колебаний. Независимый от времени множитель – комплексная функция
– круговая частота собственных колебаний. Независимый от времени множитель – комплексная функция 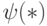 – является решением стационарного уравнения Шредингера
– является решением стационарного уравнения Шредингера
 |
( 8.3) |
 – известный дифференциальный оператор Гамильтона для данной конкретной системы,
– известный дифференциальный оператор Гамильтона для данной конкретной системы,  – действительное число (энергия квантового объекта), а на функцию
– действительное число (энергия квантового объекта), а на функцию 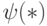 наложено условие нормирования квадрата ее модуля на единицу. Решение такого уравнения – это известная задача Штурма-Лиувилля на собственные значения. Спектр энергии может быть дискретным или непрерывным. Когда квантовый объект находится в связанном состоянии (например, электрон в кулоновском поле ядра атома) и
наложено условие нормирования квадрата ее модуля на единицу. Решение такого уравнения – это известная задача Штурма-Лиувилля на собственные значения. Спектр энергии может быть дискретным или непрерывным. Когда квантовый объект находится в связанном состоянии (например, электрон в кулоновском поле ядра атома) и  , то спектр энергии всегда дискретный, т.е. уравнение (8.3) имеет решения лишь при определенных значениях энергии
, то спектр энергии всегда дискретный, т.е. уравнение (8.3) имеет решения лишь при определенных значениях энергии  .
.Если на квантовый объект действует внешнее силовое поле, изменяющееся во времени, то эволюция волновой функции под действием этого поля описывается нестационарным уравнением Шредингера
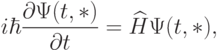 |
( 8.4) |
где 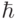 – приведенная постоянная Планка, а в оператор Гамильтона
– приведенная постоянная Планка, а в оператор Гамильтона  как слагаемое входит оператор внешнего силового поля, изменяющегося во времени.
как слагаемое входит оператор внешнего силового поля, изменяющегося во времени.
Еще одной важной для данной темы особенностью квантовой физики является более глубокое понимание процессов наблюдения. В классической физике считалось, что за физическим объектом можно наблюдать и выполнять измерения его характеристик, не влияя на его состояние. Однако на самом деле наблюдение или измерение возможны лишь в результате прямого или опосредствованного взаимодействия соответствующего сенсора с объектом. В квантовой физике понимание этого стало принципиальным, так как во время взаимодействия квантового объекта с сенсором их надо рассматривать уже как единую систему и в уравнения (8.3) и (8.4) к оператору Гамильтона  надо прибавить соответствующий квантовый оператор взаимодействия.
Из-за этого решение уравнения Шредингера и волновая функция квантового объекта изменяются. Во многих случаях процесс измерения является кратковременным взаимодействием, оператор взаимодействия зависит от времени и, следовательно, состояние объекта и поведение всей системы описываются нестационарным уравнением Шредингера (8.4). Если измерительное устройство включено постоянно, для стационарного уравнения (8.3) принципиально важным становится то, что объект перестал быть консервативным, а является уже одной из составляющих частей квантовой системы "объект + сенсор".
надо прибавить соответствующий квантовый оператор взаимодействия.
Из-за этого решение уравнения Шредингера и волновая функция квантового объекта изменяются. Во многих случаях процесс измерения является кратковременным взаимодействием, оператор взаимодействия зависит от времени и, следовательно, состояние объекта и поведение всей системы описываются нестационарным уравнением Шредингера (8.4). Если измерительное устройство включено постоянно, для стационарного уравнения (8.3) принципиально важным становится то, что объект перестал быть консервативным, а является уже одной из составляющих частей квантовой системы "объект + сенсор".
Важным является также то, что в результате взаимодействия, вообще говоря, наблюдается не то состояние квантового объекта, которое он имел до взаимодействия, а то, в которое он перешел.
При наблюдениях или измерениях состояния квантовых объектов, выполняемых с помощью классических сенсоров, действует следующее "правило редукции": сразу после наблюдения или измерения квантовый объект оказывается в том базовом состоянии, которое было только что зафиксировано.
