|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Сверхпроводниковая электроника
1.1. Справка из общего курса физики
Напомним, что при очень низких температурах, ниже т.н. "критической температуры" TK (для каждого сверхпроводящего материала она своя), ряд металлов и сплавов (в частности ниобий и его аналоги, используемые чаще всего), а в последние десятилетия также и ряд керамических материалов становятся сверхпроводящими, т.е. не оказывают совсем никакого сопротивления прохождению электрического тока. Кроме того, из толщи сверхпроводника магнитное поле вытесняется: индукция магнитного поля внутри сверхпроводника равна нулю. Однако, когда внешнее магнитное поле становится достаточно сильным, выше "критического" значения BK, то состояние сверхпроводимости "разрушается". Разрушается оно и в случае, если плотность электрического тока в сверхпроводнике превышает некоторое "критическое" значение jK.
Поскольку электрическое сопротивление сверхпроводника равно нулю, то в замкнутом сверхпроводящем контуре электрический ток может бесконечно долго циркулировать без затухания при отсутствии любой посторонней ЭДС.
Сверхпроводимость объясняется тем, что при определенных условиях двум электронам с противоположно направленными спинами становится энергетически выгоднее объединиться в неразрывную пару. Такие связанные между собой электроны называют "куперовскими парами" (в честь ученого Л. Купера, который впервые показал, что электроны в сверхпроводниках объединяются в пары). Каждая пара связанных электронов ведет себя как квазичастица с нулевым спином и с электрическим зарядом, равным двум зарядам электрона. Куперовские пары, как и всякая квантовая система, могут находиться лишь в разрешенных энергетических состояниях. Для перехода в другое разрешенное энергетическое состояние нужна значительная энергия. Поэтому куперовские пары не могут рассеиваться на фононах, примесных атомах, ионах, дефектах кристаллической решетки, из-за чего и исчезает электрическое сопротивление.
На квазичастицы с нулевым спином не распространяется квантово-механический принцип Паули, и все они находятся в одном и том же квантовом состоянии, описываются общей волновой функцией, другими словами, являются когерентными. Именно благодаря этому в сверхпроводниках для куперовских пар электронов имеет место т.н. "макроскопическая квантовая интерференция". Она приводит к тому, что магнитный поток, пронизывающий отверстие контура, "квантуется", т.е. должен быть кратным характерной величине
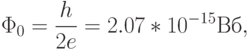 |
( 1.1) |
где 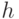 и
и  – известные физические константы (постоянная Планка и заряд электрона). Эту величину называют "квантом магнитного потока" или "флюксоном", а замкнутые контуры из сверхпроводников с включенными в них т.н. переходами Джозефсона – сверхпроводящими квантовыми интерферометрами или сокращенно "сквидами" (от англ. "SQUID" – "Superconducting Quantum Interference Device").
– известные физические константы (постоянная Планка и заряд электрона). Эту величину называют "квантом магнитного потока" или "флюксоном", а замкнутые контуры из сверхпроводников с включенными в них т.н. переходами Джозефсона – сверхпроводящими квантовыми интерферометрами или сокращенно "сквидами" (от англ. "SQUID" – "Superconducting Quantum Interference Device").
1.2. Сверхпроводящая элементная база на криотронах
Существование "критического" значения напряженности магнитного поля ВK, при превышении которого состояние сверхпроводимости исчезает, позволило создать довольно эффективные криоэлектронные вентили, которые были названы криотронами. Структура простейшего криотрона показана на рис. 1.1.а.
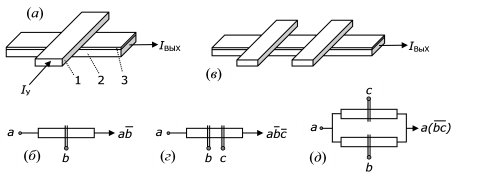
Рис. 1.1. (а) Структура простейшего криотрона; (б) его логическая схема; (в) криотрон с двумя управляющими шинами; (г) его логическая схема; (д) пример логической схемы на криотронах; 1 – сверхпроводник с большим значением ВК; 2 – сверхпроводник с меньшим значением ВK; 3 – изолирующий слой
Он состоит из сверхпроводящей шины 1 из материала с большим значением критического магнитного поля ВK (например, из ниобия) и ортогональной к ней сверхпроводящей шины 2 из материала со значительно меньшим значением ВK (например, из тантала), которые гальванически разделены тонким слоем изолятора 3. Первая сверхпроводящая шина (1) считается управляющей, вторая (2) – управляемой. Через управляющую шину пропускают электрический ток Іy такой величины, чтобы создаваемое им магнитное поле превышало критическое значение ВK для шины 2. В этом случае состояние сверхпроводимости в ней разрушается, и электрический ток сквозь нее резко уменьшается. Геометрические размеры и материал сверхпроводящих шин можно подобрать так, чтобы выходной ток был значительно больше управляющего тока и был достаточным для управления одновременно несколькими криотронами последующей логической цепи.
Если считать наличие сверхпроводящего состояния и протекание сквозь управляемую шину значительного тока логической "1", а разрушенное состояние сверхпроводимости и протекание незначительного тока –логическим "0", то соответствующая логическая схема простейшего криотрона будет выглядеть так, как показано на рис. 1.1.б. Управляемая шина изображена здесь прямоугольником, а управляющая – двойной чертой. Значительный ток сквозь криотрон течет лишь в том случае, когда на вход  криотрона подается значительный ток (
криотрона подается значительный ток (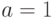 ) и одновременно в управляющей шине ток незначителен (
) и одновременно в управляющей шине ток незначителен (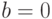 ). Реализуется логическая операция
). Реализуется логическая операция  . На рис. 1.1.в показан криотрон с двумя управляющими шинами, а на рис. 1.1.г – соответствующая ему логическая схема. Еще один вариант логической схемы на криотронах показан на рис. 1.1.д.
. На рис. 1.1.в показан криотрон с двумя управляющими шинами, а на рис. 1.1.г – соответствующая ему логическая схема. Еще один вариант логической схемы на криотронах показан на рис. 1.1.д.
Другой, более удобный для практики вариант логики на криотронах показан на рис. 1.2.
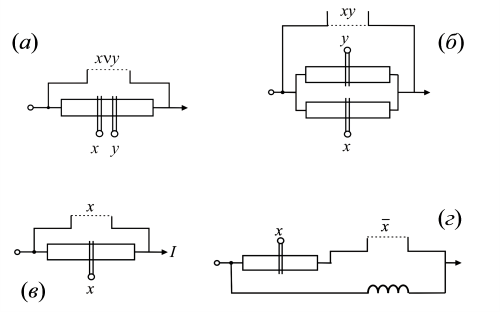
Рис. 1.2. Логические схемы на криотронах с альтернативной выходной ветвью: (а) элемент, реализующий дизъюнкцию; (б) элемент, реализующий конъюнкцию; (в) элемент, реализующий тождество (повторитель); (г) элемент, реализующий отрицание
Здесь параллельно каждой управляемой шине включена альтернативная ветвь. Когда управляемая шина находится в сверхпроводящем состоянии, через альтернативную ветвь ток не течет (или течет очень незначительный ток). Это состояние считают логическим "0". Когда в управляемой шине состояние сверхпроводимости разрушается, то электрический ток течет через альтернативную ветвь. Это состояние считают логической "1". В схеме на рис. 1.2.а ток в выходной ветви ( ) течет в тех случаях, когда хотя бы через одну из управляющих шин (
) течет в тех случаях, когда хотя бы через одну из управляющих шин ( ) течет сверхпроводящий ток, разрушающий сверхпроводимость в управляемой ветви. На рис. 1.2.б показана схема, реализующая конъюнкцию. Ток в выходной ветви (
) течет сверхпроводящий ток, разрушающий сверхпроводимость в управляемой ветви. На рис. 1.2.б показана схема, реализующая конъюнкцию. Ток в выходной ветви ( ) течет лишь в том случае, когда через каждую из управляющих шин (
) течет лишь в том случае, когда через каждую из управляющих шин ( ) течет ток, разрушающий сверхпроводимость в соответствующей управляемой шине. На рис. 1.2.в показана схема, реализующая логическую операцию тождества, а на рис. 1.2.г – схема, реализующая логическую операцию отрицания. Электрический ток, который течет через выходную ветвь, используется для управления другими криотронами или для считывания результата логических преобразований.
) течет ток, разрушающий сверхпроводимость в соответствующей управляемой шине. На рис. 1.2.в показана схема, реализующая логическую операцию тождества, а на рис. 1.2.г – схема, реализующая логическую операцию отрицания. Электрический ток, который течет через выходную ветвь, используется для управления другими криотронами или для считывания результата логических преобразований.
В целом перечисленные элементы образуют технически полную систему логических элементов, т.е. из них можно построить любую логическую схему, а также элементы памяти, триггеры, процессоры.
Принцип действия криотронов допускает их масштабирование до нанометровых размеров. Чем меньше размеры криотронов, тем меньшие токи они потребляют и, соответственно, тем меньше рассеивают тепла. Собственное время их переключения можно оценить по формуле
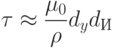 |
( 1.2) |
где  = 1,257*10-6 Гн/м – магнитная постоянная;
= 1,257*10-6 Гн/м – магнитная постоянная; 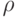 – удельное сопротивление материала управляемой шины в нормальном (не сверхпроводящем) состоянии;
– удельное сопротивление материала управляемой шины в нормальном (не сверхпроводящем) состоянии;  – толщина управляющей шины;
– толщина управляющей шины;  – толщина слоя изолятора. При
– толщина слоя изолятора. При  и
и 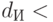 100 нм собственное время переключения может быть меньше 10 пс. Реальное быстродействие криотронных логических схем зависит от электрической емкости межсоединений и даже при нанометровых размерах криотронов не превышает нескольких гигагерц. Для современных требований это маловато.
100 нм собственное время переключения может быть меньше 10 пс. Реальное быстродействие криотронных логических схем зависит от электрической емкости межсоединений и даже при нанометровых размерах криотронов не превышает нескольких гигагерц. Для современных требований это маловато.
При всех своих положительных характеристиках – малая потребляемая мощность, высокие потенциально возможные плотность компоновки и уровень интеграции, – наноразмерные пленочные криотроны, кроме далеко не рекордного быстродействия, имеют такой недостаток, как работоспособность лишь при низких температурах.
1.3. Переходы и эффекты Джозефсона.
В 1962 г. Б. Джозефсон, позднее ставший лауреатом Нобелевской премии, показал, что определенный сверхпроводящий ток может протекать, не встречая сопротивления, также и через тонкий туннельный барьер между двумя сверхпроводниками (рис. 1.3.а). Такие барьеры стали называть "переходами Джозефсона" (далее мы употребляем сокращение "ПД").
На практике применяют обычно один из нескольких типов ПД. Чаще всего это очень тонкий (1-2 нм) слой окисла между двумя металлическими сверхпроводниками, – структура SIS (сверхпроводник – изолятор – сверхпроводник). Другой тип имеет структуру SNS (сверхпроводник – нормальный металл – сверхпроводник). Слой нормального металла может иметь толщину уже порядка 10 нм. Третий тип это SFS (сверхпроводник – ферромагнетик – сверхпроводник). Имеются и другие.
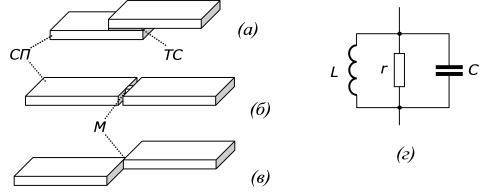
Рис. 1.3. Возможные варианты структуры перехода Джозефсона (а, б, в) и его эквивалентная электрическая схема (г): СП – сверхпроводник; TС – туннельный слой; М – "мостик" между сверхпроводниками; С – электроемкость; L – нелинейная индуктивность; r – активное сопротивление (становится существенным, когда ток сквозь переход превышает Ik)
Позднее выяснилось, что ПД может возникать при наличии любого "слабого" контакта между сверхпроводниками. Из них чаще всего используют т.н. "мостик" – тонкую перемычку между двумя планарными сверхпроводниками, размер которой меньше "длины когерентности" (среднее расстояние между связанными электронами куперовской пары, рис. 1.2.б,в).
Энергетическая диаграмма ПД для куперовских пар электронов показана на рис. 1.4: слева – для случая, когда напряжение на переходе равно нулю, справа – для случая, когда оно отличается от нуля.
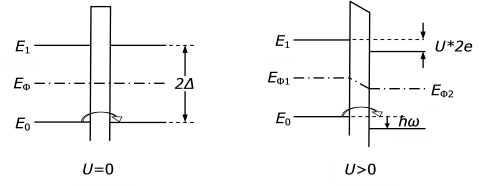
Рис. 1.4. Энергетические диаграммы перехода Джозефсона для куперовских пар: слева – когда напряжение на ПД U = 0, справа – когда U>0
Здесь вдоль вертикали отложена энергия, вдоль горизонтали – координата.  – это наиболее низкий разрешенный уровень энергии для куперовской пары,
– это наиболее низкий разрешенный уровень энергии для куперовской пары, 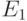 – следующий разрешенный уровень,
– следующий разрешенный уровень,  – это ширина "запрещенной зоны" ("энергетической щели") между этими уровнями. Через
– это ширина "запрещенной зоны" ("энергетической щели") между этими уровнями. Через  обозначен уровень Ферми. При отсутствии напряжения на ПД уровни Ферми слева и справа от ПД совпадают, и, если переход достаточно тонок, то куперовские пары благодаря туннельному эффекту могут проникать сквозь него.Критический ток
обозначен уровень Ферми. При отсутствии напряжения на ПД уровни Ферми слева и справа от ПД совпадают, и, если переход достаточно тонок, то куперовские пары благодаря туннельному эффекту могут проникать сквозь него.Критический ток 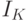 сквозь ПД как правило значительно меньше, чем критический ток в соответствующем сверхпроводнике, и равен
сквозь ПД как правило значительно меньше, чем критический ток в соответствующем сверхпроводнике, и равен
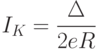 |
( 1.3) |
где  – электрическое сопротивление ПД в нормальном (не сверхпроводящем) состоянии.
– электрическое сопротивление ПД в нормальном (не сверхпроводящем) состоянии.
Между волновыми функциями куперовских пар с обеих сторон барьера в результате туннельного обмена устанавливается некоторая разность фаз  , которая и определяет величину электрического сверхпроводящего тока сквозь ПД:
, которая и определяет величину электрического сверхпроводящего тока сквозь ПД:
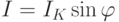 |
( 1.4) |
Когда сквозь ПД электрический ток не течет, тогда разность фаз  , а когда течет максимально допустимый сверхпроводящий ток
, а когда течет максимально допустимый сверхпроводящий ток  , то
, то 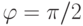 . Пока
. Пока  , напряжение на ПД равно нулю. Все это вместе называют стационарным эффектом Джозефсона.
, напряжение на ПД равно нулю. Все это вместе называют стационарным эффектом Джозефсона.
Если сквозь ПД пропускать электрический ток  , то часть его
, то часть его  будет переноситься не куперовскими парами, а обычными (попарно не связанными) электронами проводимости. Поскольку для этой части тока (не сверхпроводящей) действует закон Ома, то на ПД появляется падение напряжения
будет переноситься не куперовскими парами, а обычными (попарно не связанными) электронами проводимости. Поскольку для этой части тока (не сверхпроводящей) действует закон Ома, то на ПД появляется падение напряжения
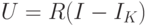 |
( 1.5) |
Б. Джозефсон показал, что, когда на переходе имеется электрическое напряжение  , то разность фаз
, то разность фаз  по законам квантовой механики начинает изменяться. Скорость изменения описывается формулой Джозефсона
по законам квантовой механики начинает изменяться. Скорость изменения описывается формулой Джозефсона
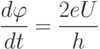 |
( 1.6) |
Интегрируя выражение (1.6) по времени, получаем
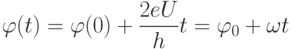 |
( 1.7) |
где
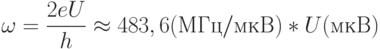 |
( 1.8) |
- т.н. "джозефсоновская частота". Подставляя (1.7) в формулу (1.4), находим, что при наличии напряжения на ПД сверхпроводящая составляющая тока через переход
 |
( 1.9) |
т.е. гармонически изменяется со временем. Это означает, что через ПД, кроме постоянного не сверхпроводящего тока  , течет сверхпроводящий переменный электрический ток с частотой (1.8), пропорциональной приложенному напряжению. Этот эффект называют нестационарным эффектом Джозефсона.
, течет сверхпроводящий переменный электрический ток с частотой (1.8), пропорциональной приложенному напряжению. Этот эффект называют нестационарным эффектом Джозефсона.
На энергетической диаграмме, изображенной на рис. 1.4 справа, этому эффекту можно поставить в соответствие процесс, в котором куперовская пара прошла сквозь ПД. На другой стороне перехода оказывается, что она имеет "избыточную" (относительно разрешенного здесь уровня) энергию  , которую она сразу же излучает в виде кванта электромагнитной волны с такой же энергией. Суммарное когерентное действие многих куперовских пар, которые проходят сквозь ПД, и предопределяет "джозефсоновскую генерацию".
, которую она сразу же излучает в виде кванта электромагнитной волны с такой же энергией. Суммарное когерентное действие многих куперовских пар, которые проходят сквозь ПД, и предопределяет "джозефсоновскую генерацию".
Переход Джозефсона лучше характеризовать не вольтамперной характеристикой, как это обычно делают, а ампер-вольтной (рис. 1.5), где вдоль оси абсцисс отложен электрический ток сквозь переход, а вдоль оси ординат – падение напряжения на переходе.
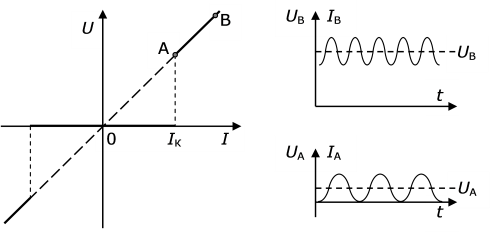
Рис. 1.5. Ампер-вольтная характеристика перехода Джозефсона (слева) и генерация переменного тока при І>Іk (справа)
Пока ток сквозь ПД не превосходит критическое значение, падения напряжения на переходе нет. Но если ток превосходит критический, на переходе падает напряжение, пропорциональное величине тока. При этом возникает джозефсоновская генерация. Типичные зависимости напряжения на переходе и тока сквозь переход показаны на рис. 1.5 справа для двух "рабочих точек" А и В, помеченных на статической характеристике слева. В рабочей точке А средний (по времени) ток равняется  , среднее напряжение на ПД
, среднее напряжение на ПД  , круговая частота колебаний тока
, круговая частота колебаний тока  . В рабочей точке В напряжение на ПД
. В рабочей точке В напряжение на ПД  , а круговая частота колебаний тока
, а круговая частота колебаний тока  .
.
Приведенные характеристики, строго говоря, касаются идеального ПД. Реальные ПД имеют дополнительно также "геометрические" емкость и индуктивность. Электрическая емкость определяется геометрическими размерами, прежде всего площадью, реального перехода Джозефсона. В ПД туннельного типа (рис. 1.3.а) она значительно больше, чем в ПД типа "мостик" (рис. 1.3.б,в). А суммарная индуктивность ПД, как коэффициент пропорциональности между ЭДС самоиндукции и скоростью изменения тока, не является постоянной, а нелинейно зависит от разности фаз  :
:
 |
( 1.10) |
Собственные электрическая емкость и индуктивность ПД могут существенно влиять на его характеристики в переходных режимах и на переменном токе. Выполнение ПД нанометровых размеров практически снимает эти проблемы.
1.4. Сквиды с переходами Джозефсона и их применение
1.4.1. Сквид с одним переходом Джозефсона
Если ПД входит в состав замкнутого сверхпроводящего контура (рис. 1.6.а), то наблюдаются дополнительные интересные эффекты. Такой контур называют сквидом с одним переходом Джозефсона.
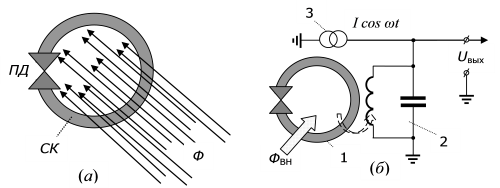
Рис. 1.6. (а) Сквид з одним переходом Джозефсона (ПД), СК – сверхпроводящий контур; Ф – магнитный поток сквозь контур. (б) схема магнитометра переменного тока, 1 – сквид с одним ПД, 2 – индуктивно связанный с ним колебательный контур, ФВН – внешний магнитный поток
Состояние такого сквида однозначно связано с величиной  суммарного магнитного потока, пронизывающего его контур. В самом деле, квантовая интерференция куперовских пар приводит к тому, что в стационарном состоянии замкнутый сверхпроводящий контур может пронизывать лишь магнитный поток, равный целому числу квантов магнитного потока
суммарного магнитного потока, пронизывающего его контур. В самом деле, квантовая интерференция куперовских пар приводит к тому, что в стационарном состоянии замкнутый сверхпроводящий контур может пронизывать лишь магнитный поток, равный целому числу квантов магнитного потока  . Поэтому сверхпроводящий ток в контуре всегда имеет такую величину, чтобы создаваемый им магнитный поток через контур дополнял (или уменьшал) магнитный поток
. Поэтому сверхпроводящий ток в контуре всегда имеет такую величину, чтобы создаваемый им магнитный поток через контур дополнял (или уменьшал) магнитный поток  , созданный внешними источниками, до величины, кратной
, созданный внешними источниками, до величины, кратной  . Если внешний магнитный поток
. Если внешний магнитный поток  начинает изменяться, то по закону магнитной индукции Фарадея в контуре возникает ЭДС, под действием которой по закону Джозефсона (1.6) начинает изменяться и разность фаз
начинает изменяться, то по закону магнитной индукции Фарадея в контуре возникает ЭДС, под действием которой по закону Джозефсона (1.6) начинает изменяться и разность фаз  на ПД. А это по закону (1.4) вызывает изменение электрического тока через ПД такое, чтобы суммарный магнитный поток сквозь контур стал кратным
на ПД. А это по закону (1.4) вызывает изменение электрического тока через ПД такое, чтобы суммарный магнитный поток сквозь контур стал кратным  .
.
Разность фаз  однозначно "отслеживает" изменения потока
однозначно "отслеживает" изменения потока  . Если это изменение очень быстрое, так что благодаря значительной ЭДС индукции ток через ПД превышает критическое значение, то излишек тока переносится обычными электронами проводимости, которые не являются когерентными к куперовских парам. При наличии не сверхпроводящего тока в контур "прорываются" дополнительные кванты магнитного потока до тех пор, пока разность
. Если это изменение очень быстрое, так что благодаря значительной ЭДС индукции ток через ПД превышает критическое значение, то излишек тока переносится обычными электронами проводимости, которые не являются когерентными к куперовских парам. При наличии не сверхпроводящего тока в контур "прорываются" дополнительные кванты магнитного потока до тех пор, пока разность  не станет меньше
не станет меньше  . Лишь тогда ток через ПД снова падает ниже критического значения, и сверхпроводящее состояние ПД восстанавливается.
. Лишь тогда ток через ПД снова падает ниже критического значения, и сверхпроводящее состояние ПД восстанавливается.
Благодаря тому, что сквид с одним ПД "реагирует" на наименьшие изменения магнитного потока, его часто используют для создания очень чувствительных сенсоров магнитного поля. Одна из наиболее распространенных схем такого сенсора, которую называют магнитометром переменного тока, показана на рис. 1.6.б. Кроме сквида 1 с одним ПД, в нем используют миниатюрный высокодобротный колебательный контур 2, индуктивно связанный со сквидом. Индуктивная связь условно изображена штриховой стрелкой. На колебательный контур от генератора 3 подают переменный ток с частотой, близкой к резонансной частоте колебательного контура 2. В этом случае импеданс контура становится очень чувствительным к магнитному потоку  . Выходным сигналом является падение переменного напряжения
. Выходным сигналом является падение переменного напряжения  на колебательном контуре.
на колебательном контуре.
1.4.2. Сквид с двумя переходами Джозефсона
Сквид с двумя ПД показан на рис. 1.7. Здесь СП – сверхпроводящие шины, ПД1 и ПД2 – переходы Джозефсона. Слева показана типичная схема применения такого сквида. Переходы Джозефсона ПД1 и ПД2 включены здесь в сверхпроводящий контур как два симметричных параллельных "плеча". В сверхпроводящем контуре циркулирует не затухающий сверхпроводящий ток  . Его направление и величина зависят от величины внешнего магнитного потока, который пронизывает контур. Ведь благодаря квантовой интерференции ток автоматически поддерживается таким, чтобы суммарный магнитный поток сквозь контур оставался кратным к
. Его направление и величина зависят от величины внешнего магнитного потока, который пронизывает контур. Ведь благодаря квантовой интерференции ток автоматически поддерживается таким, чтобы суммарный магнитный поток сквозь контур оставался кратным к  .
.
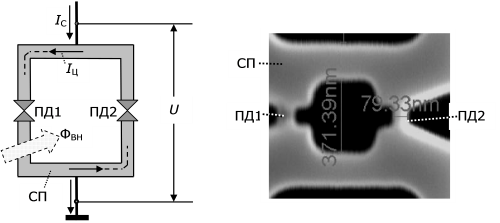
Рис. 1.7. Сквид с двумя переходами Джозефсона (ПД1 и ПД2), СП – сверхпроводящие шины. Слева – схема применения, справа – микрофотография одного из вариантов наноразмерного сквида, полученная с помощью растрового электронного микроскопа
Кроме того, извне в контур подается постоянный "ток смещения"  , который иногда называют еще "транспортным током". В результате через ПД1 течет электрический ток
, который иногда называют еще "транспортным током". В результате через ПД1 течет электрический ток  , а через ПД2 – электрический ток
, а через ПД2 – электрический ток  . Если в одном из плеч величина тока превышает критический ток ПД, то сверхпроводимость разрушается, ток смещения переключается в другое плечо, из-за чего и здесь сверхпроводимость разрушается. И на сквиде наблюдается падение напряжения
. Если в одном из плеч величина тока превышает критический ток ПД, то сверхпроводимость разрушается, ток смещения переключается в другое плечо, из-за чего и здесь сверхпроводимость разрушается. И на сквиде наблюдается падение напряжения  .
.
Благодаря квантовой интерференции падение напряжения зависит от величины внешнего магнитного потока  , который пронизывает контур. И зависимость эта является периодической с периодом, равным кванту магнитного потока
, который пронизывает контур. И зависимость эта является периодической с периодом, равным кванту магнитного потока  (рис. 1.8 слева). Эту зависимость называют сигнальной кривой. Амплитуда и положение сигнальной кривой зависят от тока смещения и от дополнительных магнитных потоков, пронизывающих сверхпроводящий контур. Справа показана функциональная схема магнитометра постоянного тока на сквиде С с двумя ПД. Величину постоянного электрического тока смещения задает генератор ГТС. Падение напряжения на сквиде воспринимается, усиливается и обрабатывается в электронном узле обработки сигналов УОС. Через катушку обратной связи КОС, магнитно-связанную со сквидом, в него подается дополнительный магнитный поток, который выбирают так, чтобы "рабочая точка" сквида всегда находилась на самом крутом участке сигнальной кривой. Благодаря этому прирост
(рис. 1.8 слева). Эту зависимость называют сигнальной кривой. Амплитуда и положение сигнальной кривой зависят от тока смещения и от дополнительных магнитных потоков, пронизывающих сверхпроводящий контур. Справа показана функциональная схема магнитометра постоянного тока на сквиде С с двумя ПД. Величину постоянного электрического тока смещения задает генератор ГТС. Падение напряжения на сквиде воспринимается, усиливается и обрабатывается в электронном узле обработки сигналов УОС. Через катушку обратной связи КОС, магнитно-связанную со сквидом, в него подается дополнительный магнитный поток, который выбирают так, чтобы "рабочая точка" сквида всегда находилась на самом крутом участке сигнальной кривой. Благодаря этому прирост  измеряемого магнитного потока дает максимальный прирост
измеряемого магнитного потока дает максимальный прирост  выходного напряжения. Это позволяет автоматически поддерживать максимальную чувствительность магнитометра.
выходного напряжения. Это позволяет автоматически поддерживать максимальную чувствительность магнитометра.
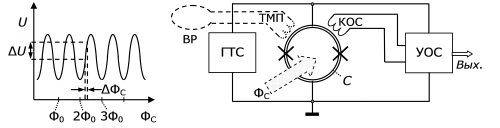
Рис. 1.8. Слева – зависимость напряжения на сквиде с двумя ПД от внешнего магнитного потока, пронизывающего сверхпроводящий контур. Справа – схема магнитометра постоянного тока: С – сквид, ГТС – генератор тока смещения, УОС –узел обработки сигналов, КОС – катушка обратной связи, ВР – выносная рамка
1.4.3. Градиометры магнитного поля
С помощью выносной рамки ВР и трансформатора магнитного потока ТМП, изображенных штриховой линией на рис. 1.8 справа, можно измерять изменения магнитного потока не только в месте непосредственного расположения сквида, но и на некотором расстоянии от него. Ведь изменения магнитного потока, пронизывающего выносную рамку, приводят к соответствующему изменению тока через катушку ТМП и связанного с ней магнитного потока сквозь контур сквида. Ориентируя выносную рамку перпендикулярно к осям ОХ, OY, OZ (рис. 1.9 слева), можно измерять изменения компонент  ,
,  и
и  магнитного потока.
магнитного потока.

Рис. 1.9. Слева – варианты ориентации выносной рамки для измерения компонент магнитного потока, ориентированных вдоль координатных осей. Справа – схема расположения пары выносных рамок для градиометра магнитного поля 1-го порядка. Обозначения как на рис. 1.8
Справа на рис. 1.9 показана схема расположения двух одинаковых выносных рамок (ВР1 и ВР2) с целью использования магнитометра постоянного тока на сквиде С с двумя ПД для измерения градиента магнитного поля. Поскольку выносные рамки ВР1 и ВР2 включены здесь навстречу одна другой, то в контур сквида трансформируется лишь разность  магнитных потоков, пронизывающих эти выносные рамки.
магнитных потоков, пронизывающих эти выносные рамки.
Зная расстояние  между ними, легко вычислить градиент магнитного потока
между ними, легко вычислить градиент магнитного потока
 |
( 1.11) |
А если расположить рядом две такие пары рамок и включить их навстречу одна другой (рис. 1.10), то магнитный поток, который трансформируется в контур сквида, будет равняться разности 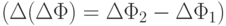 .
.
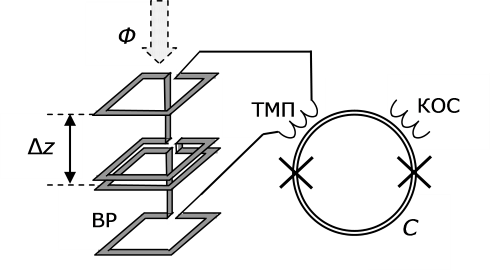
Рис. 1.10. Схема расположения двух пар выносных рамок для градиометра магнитного поля 2-го порядка. Обозначения как на рис. 1.8
Зная расстояние  между парами рамок, легко вычислить производную магнитного потока 2-го порядка
между парами рамок, легко вычислить производную магнитного потока 2-го порядка
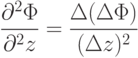 |
( 1.12) |
Магнитометры постоянного тока на сквиде С с двумя ПД в таких случаях называют градиометрами 1-го и 2-го порядка.
1.4.4. Измерение слабых магнитных полей
Чувствительность магнитометров характеризуют минимальным изменением магнитного потока, которое можно зафиксировать, отнесенным к единичной частотной полосе. Сейчас чувствительность наилучших сверхпроводящих магнитометров достигает  . Чувствительность относительно магнитной индукции достигает 10-14 Тл. И очень важно, что чувствительность эта не зависит от уровня постоянной составляющей магнитного поля, т.е. совсем небольшие изменения можно измерять на фоне относительно сильного постоянного магнитного поля, например, магнитного поля Земли.
. Чувствительность относительно магнитной индукции достигает 10-14 Тл. И очень важно, что чувствительность эта не зависит от уровня постоянной составляющей магнитного поля, т.е. совсем небольшие изменения можно измерять на фоне относительно сильного постоянного магнитного поля, например, магнитного поля Земли.
Как мы уже отмечали, физические принципы работы сквидов допускают их масштабирование, т.е. уменьшение их размеров вплоть до значений порядка длины когерентности куперовских пар (порядка 10 нм). С помощью наноразмерных сквидов удается измерять предельно слабые магнитные поля, создаваемые даже отдельными наночастицами. Принцип измерения показан на рис. 1.11 слева, где изображены сверхпроводящий контур наноразмерного сквида с двумя ПД и ряд случайно расположенных магнитных наночастиц (МНЧ).

Рис. 1.11. Слева – схема измерения магнитного поля отдельных наночастиц (НЧ). Справа – микрофотография в сканирующем электронном микроскопе магнитной наночастицы (МНЧ) диаметром 165 нм на краю сквида. ПД – переходы Джозефсона (здесь "мостики")
Магнитное поле наночастиц, расположенных внутри контура, замыкается в нем и поэтому не создает дополнительный магнитный поток сквозь контур. Магнитное поле наночастиц, расположенных на краю сверхпроводящего контура (оно условно показано пунктирными линиями) с одной стороны пронизывает контур, а с другой проходит мимо него и потому создает дополнительный магнитный поток, который можно измерять. Пример реализации измерения показан на рис. 1.11 справа. Сверхпроводящий контур с внутренним отверстием  нм сделан здесь из ниобия, переходы Джозефсона (ПД) выполнены в виде "мостиков". Магнитная наночастица (МНЧ) диаметром 165 нм из сплава железа с платиной размещена на краю сверхпроводящего контура с помощью прецизионного зондового манипулятора.
нм сделан здесь из ниобия, переходы Джозефсона (ПД) выполнены в виде "мостиков". Магнитная наночастица (МНЧ) диаметром 165 нм из сплава железа с платиной размещена на краю сверхпроводящего контура с помощью прецизионного зондового манипулятора.
Уже в 2009 г. можно было регистрировать магнитные поля от наночастиц с магнитным моментом порядка 100 магнетонов Бора. Сейчас считается возможной регистрация с помощью магнитометров на сквидах магнитных полей от отдельных молекул и даже атомов.
1.5. Многоканальные магнитометры на сквидах
1.5.1. Магнитокардиографы
На базе сверхчувствительных магнитометров на сквидах создан целый ряд многоканальных интеллектуальных сенсоров. Одним из показательных примеров являются магнитокардиографы – интеллектуальные сенсоры, позволяющие регистрировать и отслеживать изменения магнитного поля, связанные с функционированием сердца, и делать на основе этого важные для медицинской диагностики выводы. В качестве примера, опишем коротко магнитокардиографический комплекс "Кардиомагскан", функциональная схема которого показана на рис. 1.12 вверху.
Многоканальный магнитометр 1 на сквидах воспринимает в четырех точках (Измерительные сквиды) вертикальную компоненту ритмических изменений магнитного поля, обусловленных работой сердца пациента, а также все три пространственные компоненты (Референтные сквиды) фонового магнитного поля, усиливает их и передает в электронный блок 2. В состав этого блока входят микропроцессор и мультиплексор, управляющие порядком считывания сигналов от разных сквидов, обрабатывающие полученные сигналы и передающие данные в виде цифровых кодов персональному компьютеру (ПК). Все сквиды находятся при температуре, ниже критической. Необходимая температура поддерживается благодаря криостату 3 с жидким гелием. Одной заправки криостата (11 л жидкого гелия) хватает для непрерывной работы магнитометра на протяжении 5 суток, т.е. ее хватает на всю рабочую неделю.
Криостат 3 и многоканальный магнитометр 1 конструктивно объединены в криогенный модуль 4. Пациент спокойно лежит на кровати, которую можно передвигать так, чтобы точно установить сквиды в нужную позицию относительно сердца пациента (рис. 1.12, внизу). С целью получения опорных сигналов с помощью электрокардиографа 5 регистрируется также стандартная электрокардиограмма. Опорные сигналы ЭКГ передаются в электронный блок 2, где используются для определения моментов считывания магнитных сигналов, связанных с работой сердца, и на ПК. Электронный блок 2 автоматически компенсирует внешнее магнитное поле, контролирует уровень жидкого гелия в криостате, вырабатывает стандартные сигналы, с помощью которых можно проверять работу и характеристики каждого из каналов, регулировать их.

Рис. 1.12. Вверху – функциональная схема магнитнокардиографа "Кардиомагскан": 1 – многоканальный магнитометр на сквидах; 2 – электронный блок; 3 – криостат с жидким гелием; 4 – криогенный модуль; ПК – персональный компьютер; 5 – электрокардиограф; 6 – программное обеспечение. Внизу – схема расположения пациента и криогенного модуля
Программное обеспечение 6 системы состоит из двух автономных пакетов программ, работа которых распределена во времени.
Первый пакет используется во время проведения измерений, а второй пакет – после проведения обследований всей группы пациентов – с целью дальнейшего детального анализа полученных результатов. Программные модули первого пакета обеспечивают прием информации от электронного блока 2, контроль ее качества и размещение в базе данных, цифровую фильтрацию полученных сигналов, прием и анализ ЭКГ сигналов, формирование и выдачу на экран ПК магнитокардиограмм, синхронизированных с электрокардиограммой. Они поддерживают также обратную связь с блоком 2 с целью автоматической оптимизации условий измерения в зависимости от конкретных обстоятельств и особенностей организма пациента, выполняют усреднение полученных данных по нескольким сердечным циклам, предоставляют возможность редактирования полученных данных квалифицированным специалистом, организуют работу с базой данных и т.д.
Второй программный пакет содержит модули анализа пространственно-временных изменений магнитного поля сердца, построение их изображения на экране монитора, вычисление ряда медико-диагностических параметров, характеризующих динамику работы участков сердца, нарушение координации сердечных ритмов и т.п. В этот пакет программ входят также модули, которые решают непростую т.н. "обратную задачу" теории поля: по пространственному распределению магнитного поля найти распределение его источников. По этим данным строятся и выводятся на экран монитора изображения источников магнитного поля (электрических токов) в соответствующем сечении сердечной мышцы в разных фазах сердечного цикла, определяется локализация в сердце аритмогенных зон и т.д. Достигается пространственная разрешающая способность (точность локализации источников сигналов) порядка 1 мм.
Магнитокардиография на основе сквидов позволяет, например, бесконтактным способом зарегистрировать работу сердца еще не родившегося ребенка, своевременно уловить угрожающие сбои в его работе.
1.5.2. Магнитоэнцефалографы и томографы
По аналогичному принципу построены также магнитоэнцефалографы, позволяющие регистрировать слабые переменные магнитные поля, связанные с работой мозга человека, обнаруживать имеющиеся там нарушения активности, локализовать места нарушений. На рис. 1.13 показаны фотографии разных вариантов конструктивной реализации магнитноэнцефалографа на сквидах. Вверху в центре на вставке показана схема расположения измерительных сквидов относительно мозга пациента. Анализ данных от разных сквидов позволяет точно локализовать участки мозговой активности.
Для исследования и диагностики мозга требуется значительно больше каналов измерения – десятки или даже сотни. Наноразмеры сквидов позволяют реализовать даже десятки тысяч каналов. Все дело в стоимости электроники и в скорости обработки сигналов. В то время, как для исследования и диагностирования работы сердца достаточным является частотный диапазон сигналов до 100 Гц, для изучения и диагностирования работы мозга человека требуется уже частотный диапазон до 1000 Гц. Поскольку магнитные сигналы от мозга значительно слабее, чем магнитные сигналы от сердца, то помещение, где расположены магнитоэнцефалографы, приходится и значительно лучше экранировать от внешних магнитных полей. В лучших современных образцах магнитоэнцефалографов положение участков мозговых нарушений тоже можно локализовать с точностью порядка 1 мм.
Уже созданы даже 200-канальные томографы на сквидах, которые позволяют снимать и исследовать условные "срезы" мозга человека.
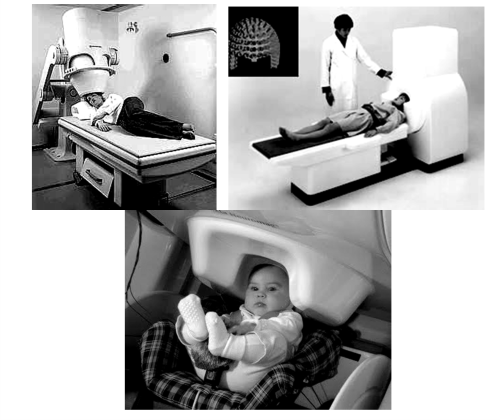
Рис. 1.13. Различные варианты реализации магнитноэнцефалографа на сквидах и схема фиксации активности отдельных участков мозга пациента (на вставке вверху в центре)
1.6. Растровые микроскопы на сквидах
Еще одним примером интеллектуальных сенсоров на сквидах является растровый сквид-микроскоп. Его общая функциональная схема показана на рис. 1.14 слева.
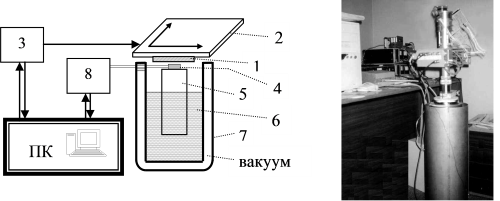
Рис. 1.14. Слева – функциональная схема растрового сквид-микроскопа: 1 – исследуемый образец, 2 – координатный стол, 3 –узел управления столом, 4 – чувствительные элементы на сквидах, 5 – хладопровод, 6 – жидкий азот или гелий, 7 – криостат, 8 – электронный блок; справа – растровый микроскоп ССМ-77
Исследуемый образец 1 устанавливают на прецизионном координатном столе 2, работой которого управляет электронный узел 3. Рядом с образцом, вплотную к нему находится микроминиатюрный магниточувствительный элемент 4 на сквидах. Чтобы поддерживать температуру ниже критической, он установлен на хладопроводе 5, конец которого погружен в жидкий азот или гелий 6 в криостате 7.
Сигналы от магниточувствительных элементов подаются в электронный блок 8, где усиливаются, фильтруются, обрабатываются и в виде цифровых кодов передаются в ПК. По командам оператора компьютер организует перемещение вдоль координат Х и Y координатного стола, на котором установлен исследуемый образец, и измерение в каждом положении, т.е. в каждой точке поверхности образца проекций вектора индукции магнитного поля и/или его градиента. Таким образом на экране монитора формируется увеличенное в десятки-тысячи раз двух- или трехмерное изображение магнитного поля объекта.
На рис. 1.14 справа приведена фотография криогенной части растрового микроскопа на сквидах ССМ-77, созданного на физическом факультете МГУ. На его основе в ИЗМИРАН России с использованием "высокотемпературных" сквидов, для охлаждения которых достаточно жидкого азота, выпускается растровый микроскоп ССМ-300. Он уже может исследовать объекты, которые находятся при обычной комнатной температуре до 300 К.
По сравнению с традиционными методами магнитной, ультразвуковой и радиографической дефектоскопии сквид-микроскопия благодаря своей сверхвысокой чувствительности позволяет обнаруживать скрытые, значительно меньшие по размерам, глубоко погруженные в материал дефекты, даже под защитным слоем. Она позволяет обнаруживать протекающие в образце коррозионные и вихревые слабые электрические токи, снимать карты токов, которые текут в многослойных электронных платах и в микросхемах. С ее помощью тестируют самые ответственные детали турбин, ракет, самолетов, осуществляют магнитные исследования геологических, минералогических, археологических образцов. Проверяют, например, подлинность купюр или важнейших документов, на которые нанесены скрытые знаки специальными магнитными чернилами и т.п. На таком микроскопе можно проводить не только пассивные, но и активные исследования, когда в исследуемом образце гальваническими, индукционными или другими методами специально возбуждают электрические или магнитные поля и изучают реакции объекта на них.
Пространственная разрешающая способность таких растровых микроскопов определяется размером магниточувствительного элемента 4 (рис. 1.14). Для достижения нанометровой разрешающей способности была разработана специальная технология формирования нанометровых сквидов на кончике зонда (англ. "SQUID on a tip"). Объясним ее с помощью рис. 1.15. Пустую внутри тонкую трубку из чистого плавленого кварца при нагревании вытягивают в сверхтонкое острие – зонд, – с двух сторон которого формируют продольные вмятины (ложбинки). После шлифовки и полировки торца на острие и на его торец в высоком вакууме напыляют алюминий, который становится сверхпроводником при температурах ниже 1,2 К.

Рис. 1.15. Слева – зонд растрового сквид-микроскопа из плавленого кварца; справа с дополнительным 500-кратным увеличением – острие этого зонда, на торце которого сформован сквид с двумя переходами Джозефсона (ПД)
Напыление осуществляют под углом так, чтобы в ложбинки алюминий не попадал. Небольшой налет удаляют химическим травлением. На торце в местах выхода вмятин образуются "слабые" мостики – два перехода Джозефсона (ПД), и возникает наносквид с диаметром отверстия около 200 нм.
Типичная сигнальная кривая магнитометра постоянного тока на таком сквиде показана на рис. 1.16 слева. Период зависимости от изменения магнитного потока (в данном случае – от изменения напряженности магнитного поля) составляет здесь около 60 мТл, амплитуда изменения напряжения – около 50 мВ, критический ток – около 1,6 мкА чувствительность в рабочей точке – около 3 В/Тл.
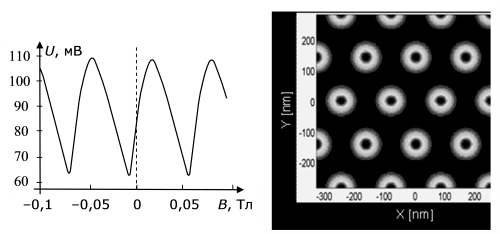
Рис. 1.16. Слева – типичная сигнальная кривая магнитометра со сквидом на торце острия диаметром 200 нм. Справа – пример изображения в растровом сквид-микроскопе, полученного с помощью такого наносквида
Справа на рис. 1.16 показан пример изображения участка экспериментального образца магнитного диска с созданной на его поверхности матрицей из наностолбиков ферромагнетика, расположенных на расстояниях 132 нм друг от друга. Как можно видеть, реальная разрешающая способность растрового микроскопа с описанным зондом существенно лучше, чем размер наносквида, и составляет около 50 нм. С его помощью удается уверенно регистрировать наночастицы с магнитным моментом до 65 магнетонов Бора (при частотном диапазоне 1 Гц).
1.7. Другие применения
1.7.1. Стандарт Вольта
Нестационарный эффект Джозефсона и формула (1.8) устанавливают точную связь между напряжением на переходе Джозефсона и частотой джозефсоновской генерации. Это было использовано в области метрологии. Очень важные для науки и техники стандарты разных физических величин имеют, к сожалению, разную точность. Наиболее точно сейчас измеряется частота, относительная точность измерения которой на высоких частотах достигает 10-14. А вот точность измерений электрического напряжения, которые базировались на эталоне из гальванических элементов, была гораздо меньше – порядка 10-6. Формула (1.8) теоретически позволила заменить измерение напряжения измерением частоты. Сложность практической реализации сверхпроводящего эталона напряжения заключалась в том, что падение напряжения на одном переходе Джозефсона очень мало – меньше 1 мВ. Однако ученым удалось изготовить микросхему из примерно 1500 последовательно соединенных переходов Джозефсона, которая дает на выходе стандартное напряжение 1 В с точностью порядка 10-10. Указанная точность, кстати, определяется здесь не точностью измерения частоты, а точностью, с которой физики знают сегодня значение отношения универсальных постоянных 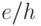 . Именно сквиды с ПД позволили значительно, приблизительно в 20 раз, повысить точность определения этого отношения, а вместе с ним и точность, с которой ученым известно значение кванта магнитного потока (1.1).
. Именно сквиды с ПД позволили значительно, приблизительно в 20 раз, повысить точность определения этого отношения, а вместе с ним и точность, с которой ученым известно значение кванта магнитного потока (1.1).
1.7.2. Радиотехнические применения
На переходах Джозефсона строят сейчас также много различных радиотехнических устройств субмиллиметрового диапазона длины волны. Это, например, параметрические усилители для названного частотного диапазона с рекордно низкими собственными шумами (т.н. "шумовая температура" составляет здесь меньше 4 К; сравните это с тем, что СВЧ усилитель на лампах бегущей волны имеет шумовую температуру порядка 10000 К). Относительно легко реализуются на этой элементной базе генераторы и приемники сигналов субмиллиметрового диапазона, модуляторы и демодуляторы, преобразователи частоты, детекторы.
Об одном из интересных применений схем на переходах Джозефсона в вычислительной технике мы расскажем вам в следующей лекции.
Контрольные вопросы
- Что такое "криотрон"? Начертите 1-2 логические схемы на криотронах и объясните, как они функционируют.
- Каких приблизительно технических параметров можно достичь в логических схемах на криотронах?
- Какие виды переходов Джозефсона (ПД) Вы знаете? Назовите их. Какие из них имеют наименьшую электрическую емкость?
- В чем заключается нестационарный эффект Джозефсона?
- Как функционирует магнитометр переменного тока? Начертите схему и объясните принцип его работы.
- Как устроен магнитометр постоянного тока? Начертите схему и объясните принцип его работы. Что такое "сигнальная кривая"?
- Какую чувствительность обеспечивают сейчас наилучшие сверхпроводящие магнитометры?
- Что такое "градиометры" магнитного поля 1-го и 2-го порядка? Объясните принцип их работы.
- Что такое "магнитокардиограф"? Как он функционирует и где применяется?
- Что такое "магнитоэнцефалограф"? Как он функционирует и где применяется?
- Как устроен растровый микроскоп на сквидах? Как формируют сквид с ПД на торце острия зонда нанометровых размеров?
- Благодаря чему сквиды с ПД позволили повысить точность измерения электрического напряжения?
Краткие итоги
Существование "критического" значения напряженности магнитного поля, при превышении которого состояние сверхпроводимости исчезает, позволило создать довольно оригинальные криоэлектронные логические вентили электрического тока, названные криотронами. Принцип действия криотронов допускает их масштабирование до нанометровых размеров. Чем меньшие размеры криотронов, тем меньшие токи они потребляют и, соответственно, тем меньше рассеивают тепла. При размерах меньше 100 нм собственное время переключения логических схем на криотронах становится меньше 10 пс.
Очень ценные для применений квантовые свойства имеют сквиды с переходами Джозефсона (ПД). Сквид с одним ПД "реагирует" на наименьшие изменения магнитного потока, поэтому его часто используют для создания очень чувствительных сенсоров магнитного поля. Одним из наиболее распространенных является магнитометр переменного тока. На сквидах с двумя ПД строят очень чувствительные магнитометры постоянного тока. Чувствительность наилучших сверхпроводящих магнитометров достигает сейчас  . Чувствительность относительно магнитной индукции достигает 10-14 Тл. И очень важно, что чувствительность эта не зависит от уровня постоянной составляющей магнитного поля, т.е. совсем небольшие изменения можно измерять на фоне относительно сильного постоянного магнитного поля, например, магнитного поля Земли.
. Чувствительность относительно магнитной индукции достигает 10-14 Тл. И очень важно, что чувствительность эта не зависит от уровня постоянной составляющей магнитного поля, т.е. совсем небольшие изменения можно измерять на фоне относительно сильного постоянного магнитного поля, например, магнитного поля Земли.
С помощью выносных рамок, индуктивно связанных с контуром сквида, можно строить магнитометры, которые измеряют все три пространственные компоненты магнитного поля, а также чувствительные градиометры 1-го, 2-го и высших порядков, которые измеряют первую, вторую или высшие производные напряженности магнитного поля по координате. С помощью наноразмерных сквидов удается измерять даже очень слабые магнитные поля, создаваемые наночастицами с магнитным моментом порядка 100 магнетонов Бора и меньше.
На базе сверхчувствительных магнитометров на сквидах создан целый ряд многоканальных интеллектуальных сенсоров. Это – магнитокардиографы, позволяющие отслеживать изменения магнитного поля, связанные с функционированием сердца, и делать на основе этого важные диагностические медицинские выводы; магнитоэнцефалографы, позволяющие регистрировать слабые переменные магнитные поля, связанные с работой мозга человека, обнаруживать имеющиеся там нарушения активности, локализовать места нарушений. Это также растровые сквид-микроскопы, позволяющие обнаруживать скрытые, глубоко погруженные в материал магнитные дефекты, даже под защитным слоем; коррозионные и вихревые слабые электрические токи, протекающие в исследуемом образце, снимать карты токов, протекающих в многослойных электронных платах и в микросхемах, и т.д. Для достижения нанометровой разрешающей способности разработана специальная технология формирования нанометровых сквидов на торце острия зонда размером порядка 100 нм.
Используя нестационарный эффект Джозефсона, удалось создать новый стандарт Вольта для метрологии с точностью порядка 10-10, а также определить отношение универсальных физических постоянных 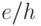 с точностью, приблизительно в 20 раз лучше, чем было известно до сих пор.
с точностью, приблизительно в 20 раз лучше, чем было известно до сих пор.
На наноразмерных переходах Джозефсона строят также много разных радиотехнических устройств субмиллиметрового диапазона длин волн: параметрические усилители с рекордно низкими собственными шумами, генераторы и приемники СВЧ радиосигналов, модуляторы и демодуляторы, преобразователи частоты, детекторы, позволяющие передавать и принимать информацию с очень высокой скоростью.
