|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Обоснование решений методами теории массового обслуживания
Входящий поток (поток требований)
Входящий поток (поток требований). Всякая обслуживающая система функционирует с целью удовлетворения заявок (требований) на обслуживание. Поэтому поток требований является одним из основных и наиболее важных понятий теории массового обслуживания.
Изучение потока требований – первая задача, возникающая как при теоретической разработке проблем массового обслуживания, так и при практическом применении ее методов к решению конкретных задач. Это нетрудно понять, если представить себе мысленно любую задачу типа массового обслуживания. Какая бы цель перед нами ни стояла, чтобы предпринять какие-то конкретные шаги по реорганизации обслуживающей системы для улучшения качества ее функционирования, мы всегда должны сначала самым тщательным образом изучить поток требований, поступающих в эту систему. Тем более важно уметь описывать поток требований количественно. Ниже приводятся математические методы, которые позволяют это делать.
Если выбрать некоторый момент времени 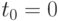 за начальный, то в ряде процессов нельзя или, по крайней мере, довольно трудно точно предсказать момент поступления следующего требования, а также моменты поступления всех следующих за ним требований.
за начальный, то в ряде процессов нельзя или, по крайней мере, довольно трудно точно предсказать момент поступления следующего требования, а также моменты поступления всех следующих за ним требований.
Процесс поступления заявок на обслуживание есть случайный процесс. Поток требований может быть описан некоторой функцией  , определяющей число требований, которые нуждаются в обслуживании (за промежуток времени
, определяющей число требований, которые нуждаются в обслуживании (за промежуток времени 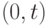 ). Функция
). Функция  — это случайная величина для каждого значения
— это случайная величина для каждого значения  . Действительно, если мы выберем промежутки времени тоже одинаковой продолжительности, то и в этом случае не можем быть уверены, что в каждой из этих промежутков поступит одинаковое число требований. Ведь за данный промежуток времени
. Действительно, если мы выберем промежутки времени тоже одинаковой продолжительности, то и в этом случае не можем быть уверены, что в каждой из этих промежутков поступит одинаковое число требований. Ведь за данный промежуток времени 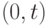 может не поступить ни одного требования, а может поступить
может не поступить ни одного требования, а может поступить 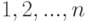 требований. Но какой бы продолжительности промежутки времени мы ни выбирали, не может быть такого положения, что в течение этого промежутка поступит 1,5 требования, 2,3 требования и так далее.
требований. Но какой бы продолжительности промежутки времени мы ни выбирали, не может быть такого положения, что в течение этого промежутка поступит 1,5 требования, 2,3 требования и так далее.
Таким образом, особенностью случайной величины, описываемой функции  , для всякого значения
, для всякого значения  является то, что она может принимать только значения целых чисел —
является то, что она может принимать только значения целых чисел — 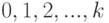 (где
(где  — целое число).
— целое число).
Очевидно, что число требований, поступивших за промежуток времени 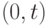 , зависит от величины этого промежутка, то есть от значения
, зависит от величины этого промежутка, то есть от значения  . Так, весьма вероятно, что, например, за минуту самолет не обнаружит ни одной подводной лодки, находящейся в районе. Вероятность необнаружения лодки за несколько часов поиска будет гораздо меньше, чем за одну минуту. Поэтому функция
. Так, весьма вероятно, что, например, за минуту самолет не обнаружит ни одной подводной лодки, находящейся в районе. Вероятность необнаружения лодки за несколько часов поиска будет гораздо меньше, чем за одну минуту. Поэтому функция  , которая определяет число требований, поступающих за время
, которая определяет число требований, поступающих за время  , зависит от параметра
, зависит от параметра  и, следовательно, является случайной функцией. Эта случайная функция принимает только целые неотрицательные значения при любых значениях
и, следовательно, является случайной функцией. Эта случайная функция принимает только целые неотрицательные значения при любых значениях  (
(  не может быть меньше нуля) и с возрастанием
не может быть меньше нуля) и с возрастанием  не убывает. Действительно, число требований, нуждающихся в обслуживании и поступающих в некоторую систему, может быть только целым положительным и с течением времени не может убывать.
не убывает. Действительно, число требований, нуждающихся в обслуживании и поступающих в некоторую систему, может быть только целым положительным и с течением времени не может убывать.
Если проделать несколько опытов и в каждом регистрировать значения  , то полученные при этом функции, как правило, не будут совпадать. Пусть
, то полученные при этом функции, как правило, не будут совпадать. Пусть  — функция, образованная значением
— функция, образованная значением  в данном опыте. Эта функция уже не является случайной. Она называется реализацией случайной функции
в данном опыте. Эта функция уже не является случайной. Она называется реализацией случайной функции  в данном опыте.
в данном опыте.
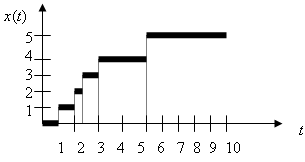
На рисунке изображена одна из реализаций случайной функции  . Если считать, что рис. 4.2 изображает график обнаружения подводных лодок (на оси
. Если считать, что рис. 4.2 изображает график обнаружения подводных лодок (на оси  отложено время в сутках, а на оси
отложено время в сутках, а на оси  — число обнаружений), то этот график означает следующее. После начала поиска в течение суток не было ни одного обнаружения. За вторые сутки было два обнаружения подводных лодок, одно в начале, а второе через 12 часов. За третьи сутки было одно обнаружение. В начале четвертых суток было еще одно обнаружение. Последнее, пятое, обнаружение было в середине пятых суток. Это, конечно, не означает, что по такому закону обнаружения будут происходить каждый раз. Поэтому функция и называется реализацией случайной функции.
— число обнаружений), то этот график означает следующее. После начала поиска в течение суток не было ни одного обнаружения. За вторые сутки было два обнаружения подводных лодок, одно в начале, а второе через 12 часов. За третьи сутки было одно обнаружение. В начале четвертых суток было еще одно обнаружение. Последнее, пятое, обнаружение было в середине пятых суток. Это, конечно, не означает, что по такому закону обнаружения будут происходить каждый раз. Поэтому функция и называется реализацией случайной функции.
Говоря более строго, в данном случае реализацией случайной функции является неслучайная функция одного аргумента времени. Для полного описания случайной функции практически невозможно определить все ее реализации, так как их может быть бесчисленное множество. Поэтому используют другой способ ее задания. Случайная функция  будет полностью определена, если для любых положительных промежутков времени
будет полностью определена, если для любых положительных промежутков времени 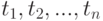 мы можем указать число требований, поступивших за каждый из этих промежутков. Но как было сказано выше, число требований, поступивших за любой из этих отрезков времени, есть величина случайная. Следовательно, нужно уметь характеризовать случайные величины. Как известно, полная характеристика случайной величины дается законом распределения. Но нам нужно знать одновременно поведение функции
мы можем указать число требований, поступивших за каждый из этих промежутков. Но как было сказано выше, число требований, поступивших за любой из этих отрезков времени, есть величина случайная. Следовательно, нужно уметь характеризовать случайные величины. Как известно, полная характеристика случайной величины дается законом распределения. Но нам нужно знать одновременно поведение функции  . За промежутки времени продолжительностью
. За промежутки времени продолжительностью 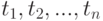 . Поэтому необходимо дать характеристику группы случайных величин
. Поэтому необходимо дать характеристику группы случайных величин 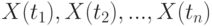 . Такой характеристикой является
. Такой характеристикой является  -мерный закон распределения группы случайных величин:
-мерный закон распределения группы случайных величин:
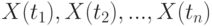 .
.
Но функция  может принимать только целые положительные значения,
может принимать только целые положительные значения,
поэтому она может быть задана более просто. Для полного определения потока требований достаточно знать, какова будет вероятность того, что за время 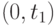 поступит
поступит  требований, за время
требований, за время 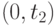 поступит
поступит  требований и так далее. Если эта вероятность будет известна для любой группы целых положительных
требований и так далее. Если эта вероятность будет известна для любой группы целых положительных 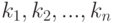 и положительных
и положительных 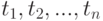 , то поток требований можно полностью описать. Эту вероятность мы будем обозначать через
, то поток требований можно полностью описать. Эту вероятность мы будем обозначать через
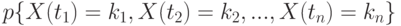 .
.
Очевидно, что эта вероятность может быть отлична от нуля только в том случае, если при 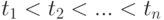 величины k_i(i=1,2,3,...n) удовлетворяют условию
величины k_i(i=1,2,3,...n) удовлетворяют условию 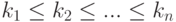 .
.
Это утверждение вытекает из того, что функция не убывает с возрастанием  . Знание функции
. Знание функции
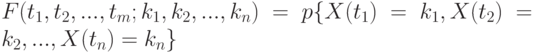
для любых 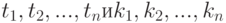 полностью определяет поток требований. Зная эти вероятности, мы всегда сможем ответить на любой вопрос о потоке требований и определить любую его характеристику. В частности, можно определить вероятность того, что за промежуток времени
полностью определяет поток требований. Зная эти вероятности, мы всегда сможем ответить на любой вопрос о потоке требований и определить любую его характеристику. В частности, можно определить вероятность того, что за промежуток времени 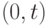 поступит
поступит 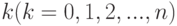 требований. Вероятность этого будет равна
требований. Вероятность этого будет равна
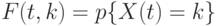 .
.
Так, например, вероятность того, что за время  не поступит ни одного требования, равна
не поступит ни одного требования, равна
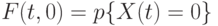 .
.
Вероятность того, что в течение суток в исследуемую систему обслуживания каждый час будет поступать только одно требование, будет равна
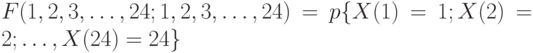 ,
,
Напомним, что все это множество можно определить при условии, что функция 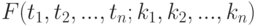 известна. Но задача отыскания такой функции в общем случае является весьма трудной.
известна. Но задача отыскания такой функции в общем случае является весьма трудной.
Таким образом, принципиально может быть описан любой поток требований. Но, как мы видели, описание не будет простым и достаточно удобным. Изучение процессов массового обслуживания при таком описании потока требований является весьма трудной задачей.
Часто на практике встречаются потоки, которые обладают свойствами, позволяющими найти более простые способы их описания. Так, многие потоки требований обладают свойством стационарности. Стационарными являются потоки, для которых вероятность поступления определенного количества требований в течение определенного промежутка не зависит от начала времени, а зависит от длины промежутка. Строго говоря, поток называется стационарным, если закон распределения группы случайных величин
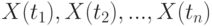
совпадает с законом распределения
 ,
,
то есть распределение случайных величин зависит от 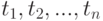 и не зависит от величин
и не зависит от величин  , где
, где  — любой произвольный отрезок времени. Как частный случай из этих рассуждений получается, что для стационарных потоков
— любой произвольный отрезок времени. Как частный случай из этих рассуждений получается, что для стационарных потоков
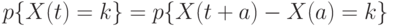 ,
,
где  , то есть вероятность того, что ровно
, то есть вероятность того, что ровно  требований будет получено за промежуток времени
требований будет получено за промежуток времени 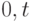 , равна вероятности получения
, равна вероятности получения  требований за промежуток времени
требований за промежуток времени 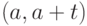 при любом значении
при любом значении  .
.
Таким образом, наличие свойства стационарности значительно облегчает изучение потока требований. Действительно, если известен характер потока требований, поступающих в обслуживающую систему с некоторого начального момента 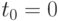 , то для того, чтобы получить характеристики потока, начиная с момента
, то для того, чтобы получить характеристики потока, начиная с момента 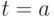 , нет необходимости изучать этот поток заново: можно воспользоваться характеристиками, полученными ранее. Число требований, поступающих в систему обслуживания после момента
, нет необходимости изучать этот поток заново: можно воспользоваться характеристиками, полученными ранее. Число требований, поступающих в систему обслуживания после момента 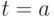 , то есть
, то есть 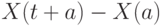 , при наличии свойства стационарности будет подчиняться тому же закону, что и
, при наличии свойства стационарности будет подчиняться тому же закону, что и  .
.
Свойством стационарности обладают многие реальные потоки требований.
В некоторых реальных потоках число требований ( поступивших в систему после произвольного момента времени  ) не зависит от того, какое число требований поступило в систему до момента
) не зависит от того, какое число требований поступило в систему до момента  . Это свойство независимости называется отсутствием последствия, или, точнее, поток требований называется потоком без последствия в тех случаях, когда закон распределения группы
. Это свойство независимости называется отсутствием последствия, или, точнее, поток требований называется потоком без последствия в тех случаях, когда закон распределения группы 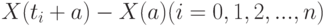 при
при  и любом
и любом  не зависит от значения величины
не зависит от значения величины  при
при  . В частности, условная вероятность поступления
. В частности, условная вероятность поступления  требований за промежуток времени
требований за промежуток времени 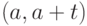 при предположении, что количество требований, поступивших в систему до
при предположении, что количество требований, поступивших в систему до  , будет любым, совпадает с безусловной вероятностью этого события.
, будет любым, совпадает с безусловной вероятностью этого события.
Свойством отсутствия последствия обладают также многие реальные потоки.
Обозначим 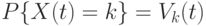 , где
, где 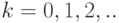 . Иными словами,
. Иными словами, 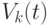 есть вероятность того, что за промежуток времени
есть вероятность того, что за промежуток времени 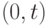 при
при  поступит точно
поступит точно  требований.
требований.
Стационарный поток без последствия имеет важное свойство: его можно полностью охарактеризовать системой функций 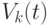 , где
, где 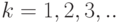 . Вероятность
. Вероятность
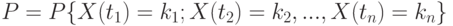
выражается через

следующим образом:
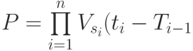 )
)
где
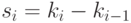 .
.
Поэтому, чтобы описать стационарный поток без последствия, достаточно получить систему функций 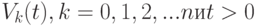 . Это свойство в значительной степени упрощает изучение таких потоков и облегчает их описание.
. Это свойство в значительной степени упрощает изучение таких потоков и облегчает их описание.
В целом ряде случаев, когда мы имеем дело с конкретной системой обслуживания, характер потока требований таков, что в любой момент времени практически может поступить только одно требование. Потоки, обладающие этим свойством, называются однородными . Свойство однородности имеет важное значение. Оно показывает, что в таких потоках невозможно (или почти невозможно) одновременное появление двух или большего числа требований.
Если обозначить через  вероятность появления за промежуток времени
вероятность появления за промежуток времени 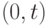 не меньше двух требований, то можно более точно сформулировать свойство однородности: поток требований называется однородным, если
не меньше двух требований, то можно более точно сформулировать свойство однородности: поток требований называется однородным, если
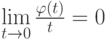
или 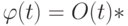 при
при 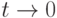 . Иными словами, вероятность того, что появится больше одного требования за малый промежуток времени
. Иными словами, вероятность того, что появится больше одного требования за малый промежуток времени  , есть бесконечно малая величина более высокого порядка, чем
, есть бесконечно малая величина более высокого порядка, чем  . Это и означает, что почти невероятно поступление двух или нескольких требований за малый промежуток времени. В некоторых реальных потоках это свойство является очевидным, а в некоторых интуитивно очевидным или, по крайней мере, справедливым с достаточно хорошим приближением к действительности.
. Это и означает, что почти невероятно поступление двух или нескольких требований за малый промежуток времени. В некоторых реальных потоках это свойство является очевидным, а в некоторых интуитивно очевидным или, по крайней мере, справедливым с достаточно хорошим приближением к действительности.
Особый интерес представляют так называемые простейшие потоки. Простейшими потоками требований называются потоки, одновременно обладающие свойствами стационарности, ординарности и отсутствия последствия. Для этих потоков значительно проще получить аналитические решения задач массового обслуживания, которые лучше изучены. Поскольку простейший поток является стационарным и у него отсутствует последствие, для его полного описания вполне достаточно знать систему функций 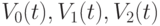 .
.
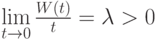 ,
,
где
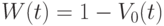 .
.
Величина  называется параметром (интенсивностью) потока. Она может быть неограниченно большой и неограниченно малой, но не может быть отрицательной. Функция
называется параметром (интенсивностью) потока. Она может быть неограниченно большой и неограниченно малой, но не может быть отрицательной. Функция 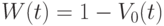 является вероятностью того, что за время
является вероятностью того, что за время  в систему поступит по крайней мере одно требование. Действительно, так как
в систему поступит по крайней мере одно требование. Действительно, так как
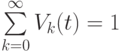 ,
,
то
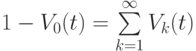 .
.
Но
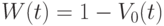 ,
,
то есть
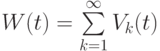 .
.
Следовательно, 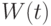 есть вероятность того, что за время
есть вероятность того, что за время  в систему поступит по крайней мере одно требование на обслуживание.
в систему поступит по крайней мере одно требование на обслуживание.
Для простейшего потока вероятность поступления равно 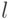 требований за время
требований за время  выражается через параметр потока
выражается через параметр потока  следующим образом:
следующим образом:
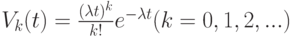 |
( 4.1) |
Таким образом, для простейшего потока число требований в промежутке  распределено по закону Пуассона с параметром
распределено по закону Пуассона с параметром  , поэтому простейший поток иногда называют стационарным пуассоновским потоком. Простейший поток полностью определяется системой функций (4.1.). Функции
, поэтому простейший поток иногда называют стационарным пуассоновским потоком. Простейший поток полностью определяется системой функций (4.1.). Функции 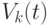 зависят только от параметра потока
зависят только от параметра потока  (если не считать
(если не считать  ). Напомним, что
). Напомним, что 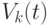 есть вероятность поступления ровно
есть вероятность поступления ровно  требований за время
требований за время 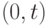 . Следовательно, чтобы дать полную характеристику простейшего потока, достаточно знать только одну величину – параметр потока.
. Следовательно, чтобы дать полную характеристику простейшего потока, достаточно знать только одну величину – параметр потока.
Рассмотрим физический смысл параметра  . Покажем, что для простейшего потока параметр
. Покажем, что для простейшего потока параметр  равен математическому ожиданию числа требований, поступивших в систему за единицу времени. Чтобы доказать это, вычислим математическое ожидание числа требований, поступивших за промежуток времени
равен математическому ожиданию числа требований, поступивших в систему за единицу времени. Чтобы доказать это, вычислим математическое ожидание числа требований, поступивших за промежуток времени 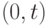 по формуле
по формуле
![M_t[k]=\sum\limits_{k=1}^{\infty}kV_k(t)=\sum\limits_{k=1}^{\infty}k\frac{(\lambda t)^k}{k!}e^{-\lambda t}=e^{-\lambda t} \lambda t \sum\limits_{k=1}^{\infty}\frac{(\lambda t)^{k-1}}{(k-1)!}](/sites/default/files/tex_cache/664ba16296506df2f33bfba6fcfe739d.png) .
.
Но сумма 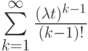 является разложением в ряд функции
является разложением в ряд функции 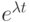 по степеням
по степеням  ,
,
поэтому
![M_t[k]=\lambda t e^{-\lambda t}e^{\lambda t}=\lambda t](/sites/default/files/tex_cache/fcca1da5d2751b3b522ac309e6a3d196.png) .
.
Таким образом, если анализ показывает, что изучаемый поток является простейшим, то для его полного описания достаточно вычислить математическое ожидание числа требований, поступивших за единицу времени.
Простейший поток обладает еще одним очень интересным свойством: для него вероятность получения в течение промежутка времени длительности  ровно
ровно  требований достигает наибольшего значения для
требований достигает наибольшего значения для 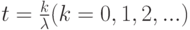 . В частности, при
. В частности, при  максимумы будут достигаться в моменты времени, равные
максимумы будут достигаться в моменты времени, равные 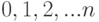 единиц времени.
единиц времени.