Цифровая модуляция

Сведения о системах модуляции

В настоящее время все абонентские терминалы преобразуют сигналы в цифровую форму. Одна из важнейших проблем, как на абонентском участке, так и участке соединительных линий обеспечить максимальную скорость передачи цифровой информации.

Существующая абонентская проводная сеть имеет громадный объем. Замена ее на более скоростную среду передачи, например, на оптоволоконную среду, подобна замене песка на всех пляжах мира и не всегда возможна по экономическим причинам.

Поэтому основная задача, которую успешно решают связисты мира увеличение пропускной способности существующей.

Всегда возникает основной вопрос, телефонная связь уже существует более 150 лет. Эта проводная сеть рассчитана на диапазон человеческого голоса или точнее на пропускание аналоговой частоты в диапазоне от 0,3 до 3,4 кГц.

Как же удалось сегодня многократно увеличить этот диапазон и сделать возможным передачу информации, которая требует ресурс в более чем 100 раз. Это достигнуто различными способами, но в основном благодаря разработке способов модуляции.

Наиболее применяемый в настоящее время класс модуляции фазовый. Мы постепенно рассмотрим этот вид. Начиная от простейших видов такой модуляции, а потом рассмотрим наиболее применяемые методы.

Многоуровневая передача сигналов

Цифровое преобразование сигналов подразумевает двоичное кодирование сигналов. Когда же нужно получить высокую скорость передачи данных в условиях ограниченной полосы прибегают к методам повышения информационной емкости передаваемых символов. Одним из таких методов является многоуровневая система, когда каждый сигнал может принимать несколько уровней амплитуды в зависимости от значения исходного символа. Скорость передачи данных в многоуровневой системе передачи равна.

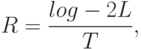( 4.1)

где

• – уровней, которые могут быть выбраны для передачи сигналов в данном интервале,
• –длительность интервала сигнала.

Скорость передачи сигнала, равная обычно называется скоростью передачи символов и измеряется в бодах. На практике понятие "бод" обычно понимают как синоним скорости в битах. Однако, строго говоря, скорость передачи в битах равна скорости передачи в бодах только в случае двоичной передачи (один бит за один интервал сигнала).

На рис.4.1 показан пример восьмиуровневого сигнала. Это позволяет увеличить скорость передачи 3 бита на сигнальный интервал (т.е. 3 бита на бод).

Рис. 4.1. Многоуровневая передача с тремя битами на сигнальный интервал

Многоуровневые передающие системы увеличивают скорость передачи данных в пределах заданной полосы частот, но требуют значительного увеличения уровня сигнал шум. Известно, что при большом уровне помех наиболее уязвима амплитуда сигнала. Поэтому такая система не получила распространения.

В современных системах примером применения такой системы может служить организация цифровой абонентской линии в системе ISDN (Integrated Services Digital Network), в которой для достижения скорости 160 кбит/с. используется четырехуровневая передача [ 2 ]

Фазовые методы модуляции

Фазовые методы модуляции XE "Фазовые методы модуляции" являются, в какой - то степени аналогами многоуровневой передачи сигналов, поскольку тоже позволяют увеличить информационную емкость передаваемого символа.

Фазовая манипуляция

Фазовая модуляция связана с манипуляцией фазы. При такой манипуляции для получения бинарного сигнала в каждом тактовом интервале используется одна из фаз, отличающаяся на 180 градусов.

Возможна также многоуровневая ФМ. Фазовая манипуляция XE "Фазовая манипуляция" в настоящее время – наиболее распространенная форма модуляции.

Популярность этого типа модуляции определяется, прежде всего, наличием постоянной огибающей, что обеспечивает то, что она нечувствительна к изменениям уровня сигнала, влиянию затухания и характеристикам аппаратуры усиления и обеспечивает хорошую характеристику. С точки зрения отношения сигнал шум () системы фазовой модуляции обеспечивают оптимальные (теоретически) значения характеристик ошибок.

Общий вид n-уровневой фазовой манипуляции отображается формулой

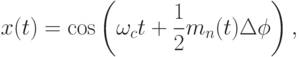( 4.1)

где

• -величина, на которую отличаются фазы соседних сигналов;
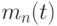• - симметричный n –уровневый сигнал "без возвращения к нулю" (NRZ – non return to zero) c уровнями и т.д.

Рис. 4.2. Фазовые манипуляции: а – 2ФМ; б – 4ФМ

На рис.4. 2 показаны примеры типичных 2-ФМ и 4-ФМ – сигналов. На рисунке скорость передачи при 4-ФМ, в два раза меньше, чем 2-ФМ, что обеспечивает одинаковую скорость передачи данных (из-за увеличения информационной емкости). На этом рисунке приведены фазовые диаграммы для косинусоидального сигнала (см. формулу 4.1).