|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Дискретное программирование
Пример математической модели дискретного программирования (транспортная задача )
Имеется  пунктов поставщиков
пунктов поставщиков  и
и  пунктов назначения (потребителей)
пунктов назначения (потребителей) 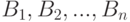 .
.
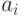 — количество груза в тоннах, сосредоточенное в пункте
— количество груза в тоннах, сосредоточенное в пункте  ;
;
 — количество груза, ожидаемое в пункте
— количество груза, ожидаемое в пункте  .
.
Принимаем условие
 |
( 6.16) |
означающее, что суммарный запас груза равен суммарной потребности в нем.
 — стоимость перевозки одной тонны груза из пункта
— стоимость перевозки одной тонны груза из пункта  в пункт
в пункт  .
.
 — количество тон груза, перевезенное из пункта
— количество тон груза, перевезенное из пункта  в пункт
в пункт  .
.
Требуется найти оптимальный план перевозок, то есть рассчитать, сколько груза должно быть отправлено из каждого пункта отправления в каждый пункт назначения, с тем условием, чтобы суммарная стоимость перевозок была наименьшей.
Неизвестными в нашей задаче являются  неотрицательных чисел
неотрицательных чисел  . Сведем их в таблицу 6.1, назовем ее матрицей перевозок.
. Сведем их в таблицу 6.1, назовем ее матрицей перевозок.
Запишем соотношение для пунктов поставщиков  и пунктов потребителей
и пунктов потребителей 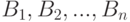 .
.
Будем называть уравнение 0I горизонтальными уравнениями, а 0II – вертикальными. Перевозка из  и
и  стоит
стоит  , общая стоимость всех перевозок будет
, общая стоимость всех перевозок будет
 |
( II) |
где суммирование производится по всем  и всем
и всем  . Таким образом, мы пришли к следующей задаче линейного программирования:
. Таким образом, мы пришли к следующей задаче линейного программирования:
Дана система уравнений I и линейная функция II. Требуется среди неотрицательных решений системы найти такое, которое минимизирует функцию II.
Метод северо-западного угла
Разберем метод на примере.
Пусть есть 3 пункта отправления

и 4 пункта назначения
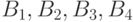 .
.
Запасы в пунктах отправления:
 .
.
Потребности:
 .
.
Занесем данные в таблицу.
Потребности пункта  удовлетворены полностью и поэтому столбец, соответствующий
удовлетворены полностью и поэтому столбец, соответствующий  , можно временно исключить из рассмотрения, то есть переходим к таблице 3.
, можно временно исключить из рассмотрения, то есть переходим к таблице 3.
Отметим, что и в таблице 6.3 сумма всех потребностей по-прежнему равна сумме всех запасов. К Таблице 6.3 применим тот же прием и попытаемся удовлетворить потребности  пункта
пункта  .(в таблице 6.3 пункт
.(в таблице 6.3 пункт  играет роль первого) запасами
играет роль первого) запасами  пункта
пункта  . Очевидно, что потребности эти удается удовлетворить лишь частично, так как
. Очевидно, что потребности эти удается удовлетворить лишь частично, так как  . При этом потребности
. При этом потребности  сократятся до
сократятся до  , а запасы
, а запасы  окажутся исчерпаны полностью. В силу этого строку, отвечающую
окажутся исчерпаны полностью. В силу этого строку, отвечающую  , из таблицы 6.3 можно временно удалить. Получим новую таблицу – таблицу 6.4, в которой имеются уже два пункта отправления
, из таблицы 6.3 можно временно удалить. Получим новую таблицу – таблицу 6.4, в которой имеются уже два пункта отправления  и
и 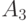 и три пункта назначения
и три пункта назначения  .
.
Аналогичным приемом продолжаем сокращать последовательно получаемые таблицы, пока не удовлетворим потребности всех пунктов назначения. В случае, когда новые запасы равны новым потребностям, можно исключить из таблицы по желанию строку и столбец. В процессе сокращения таблиц мы получим следующие значения для некоторых из неизвестных:
 .
.
Вписав их в таблицу 6.2, получим таблицу 6.5.
Условимся называть те клетки таблицы 6.5, в которые вписаны значения неизвестных, — базисными, а остальные клетки — свободными. Если считать, что значения неизвестных  , которые отвечают свободным клеткам, равны нулю, то получившийся набор значений всех неизвестных дает допустимое решение рассматриваемой задачи.
, которые отвечают свободным клеткам, равны нулю, то получившийся набор значений всех неизвестных дает допустимое решение рассматриваемой задачи.
Действительно, легко проверить, что сумма значений неизвестных в каждой строке таблицы равна запасу в соответствующем пункте отправления, а в каждом столбце – потребности в соответствующем пункте назначения. Поэтому уравнения I, II удовлетворяются.
В качестве примера прикладных задач дискретного программирования можно рассмотреть следующие задачи.
- Задачи планирования перевозок.
- Задачи размещения и специализации.
- Задачи логического проектирования.
- Задачи теории расписаний.
- Другие прикладные задачи.



















 (так как переслали в
(так как переслали в