Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3115 / 710 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Лекция 10: Многометрическая (многомерная) оптимизация. Методы многомерной оптимизации: метод Хука – Дживса, метод Нелдера – Мида, метод полного перебора, метод покоординатного спуска, метод градиентного спуска

A

|

версия для печати

2. Метод Нелдера – Мида.

Метод Нелдера — Мида (называется также поиском по деформируемому многограннику) является развитием симплексного метода Спендли, Хекста и Химсворта. Множество (n + 1) -й равноудаленной точки в n -мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. Следовательно, в двумерном пространстве симплексом является равносторонний треугольник, а в трехмерном пространстве — правильный тетраэдр. Идея метода состоит в сравнении значений функции в (n + 1) вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенном первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самых эффективных, если $n \le 6$ .

В методе Спендли, Хекста и Химсворта симплекс перемещается с помощью трех основных операций: отражения, растяжения и сжатия. Смысл этих операций станет понятным при рассмотрении шагов процедуры.

A. Найдем значения функции f₁=f(x₁),f₂=f(x₂) ... f_n+1=f(х_n+1) в вершинах симплекса.

Б. Найдем наибольшее значение функции f_h, следующее за наибольшим значением функции f_g наименьшее значение функции f_l и соответствующие им точки x_h, x_g, x_l.

B. Найдем центр тяжести всех точек, за исключением точки х_h. Пусть центром тяжести будет

$x_0 = \frac{1}{n} \sum_{i \neq h} x_i$

( 2.1)

и вычислим f(x₀)=f₀.

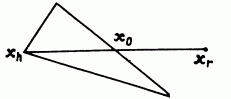
Г. Удобнее всего начать перемещение от точки x_h. Отразив точку x_h относительно точки х₀, получим точку х_r и найдем f(x_r) = f_r. Операция отражения иллюстрируется рис.10.3. Если а > 0 - коэффициент отражения, то положение точки х_r определяется следующим образом:

т.е.

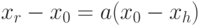
( 2.2)

Замечание: a = | x_r – x_0 | / | x_0 - x_h |

Д. Сравним значения функций f_r и f_l.

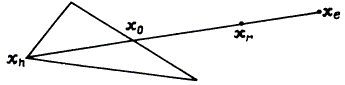
1. Если f_r < f_l, то мы получили наименьшее значение функции. Направление из точки x₀ в точку x_r наиболее удобно для перемещения. Таким образом, мы производим растяжение в этом направлении и находим точку x_e и значение функции f_e = f(x_e). Рисунок 10.4 иллюстрирует операцию растяжения симплекса.

Рис. 10.3.

Рис. 10.4.

Коэффициент растяжения $\gamma > 1$ можно найти из следующих соотношений:

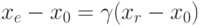
$x_e - x_0 = \gamma (x_r - x_0)$

т.е.

$x_e = \gamma x_r + (1 - \gamma) x_0$

( 2.3)

Замечание: $\gamma = | x_e – x_0 | / | x_r – x_0 |$

а) Если f_e < f_l, то заменяем точку x_h на точку x_e и проверяем (n + 1) -ую точку симплекса на сходимость к минимуму (см. шаг И). Если сходимость достигнута, то процесс останавливается; в противном случае возвращаемся на шаг Б.

б) Если f_e > f_l, то отбрасываем точку x_e. Очевидно, мы переместились слишком далеко от точки x₀ к точке x_r. Поэтому следует заменить точку x_h на точку x_r, в которой было получено улучшение (шаг Д, 1), проверить сходимость и, если она не достигнута, вернуться на шаг Б.

2. Если f_r > f_l, но f_r < f_g, то x_r является лучшей точкой по сравнению с другими двумя точками симплекса и мы заменяем точку x_h на точку x_r и, если сходимость не достигнута, возвращаемся на шаг Б, т.е. выполняем пункт 1,6, описанный выше.

3. Если f_r > f_l и f_r > f_g, перейдем на шаг Е.

Е. Сравним значения функций f_r и f_h.

1. Если f_r > f_h, то переходим непосредственно к шагу сжатия Е,2.

Если f_r < f_h, то заменяем точку x_h на точку x_r и значение функции f_h на значение функции f_r. Запоминаем значение f_r > f_g из шага Д,2, приведенного выше. Затем переходим на шаг Е,2.

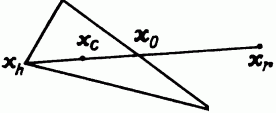
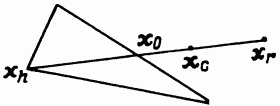
2. В этом случае f_r > f_h, поэтому ясно, что мы переместились слишком далеко от точки x_h к точке x₀. Попытаемся исправить это, найдя точку x_c (а затем f_c ) с помощью шага сжатия, показанного на рис. 10.5. Если f_r > f_h, то сразу переходим к шагу сжатия и находим точку x_c из соотношения

$x_c - x_0 = \beta (x_h - x_0)$

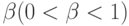где $\beta (0 < \beta < 1)$ - коэффициент сжатия. Тогда

$x_c = \beta x_h + (1 - \beta) x_0$

( 2.4)

Если f_r < f_h, то сначала заменим точку x_h на точку x_r, а затем произведем сжатие. Тогда точку x_c найдем из соотношения

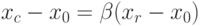
$x_c - x_0 = \beta(x_r - x_0)$

т.е.

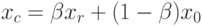$x_c = \beta x_r + (1-\beta) x_0$

( 2.5)

(рис. 10.6).

Рис. 10.5.

Рис. 10.6.

Ж. Сравним значения функций f_c и f_h.

1. Если f_c < f_h, то заменяем точку x_h на точку x_c и если сходимость не достигнута, то возвращаемся на шаг Б.

2. Если f_c > f_h, то очевидно, что все наши попытки найти значение меньшее f_h закончились неудачей, поэтому мы переходим на шаг 3.

3. На этом шаге мы уменьшаем размерность симплекса делением пополам расстояния от каждой точки симплекса до x₁ - точки, определяющей наименьшее значение функции.

Таким образом, точка x_j заменяется на точку x_l = (x_l + x_i)/2, т.е. заменяем точку x_i точкой (x_i - x_l)/2 (2.6). Затем вычисляем f_i для i = 1, 2, ...,(n+1), проверяем сходимость и, если она не достигнута, возвращаемся на шаг В.

И. Проверка сходимости основана на том, чтобы стандартное отклонение (n + 1) -го значения функции было меньше некоторого заданного малого значения е. В этом случае вычисляется

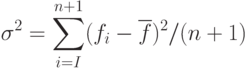$\sigma^2 = \sum_{i=I}^{n+1} (f_i - \overline{f})^2 / (n+1)$

( 2.7)

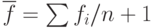где $\overline{f} = \sum f_i / n+1$ .

Если $\sigma < e$ , то все значения функции очень близки друг к другу, и поэтому они, возможно, лежат вблизи точки минимума функции x_l. Исходя из этого, такой критерий сходимости является разумным, хотя Бокс, Дэвис и Свенн предлагают то, что они считают более "безопасной" проверкой.

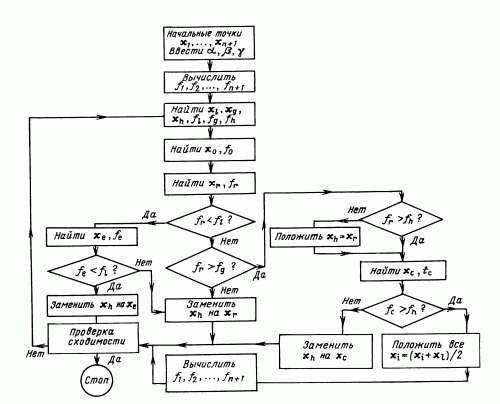
Шаги этой процедуры представлены в виде блок-схемы на рис. 10.7.

Коэффициенты $\alpha, \beta, \gamma$ в вышеприведенной процедуре являются соответственно коэффициентами отражения, сжатия и растяжения. Нелдер и Мид рекомендуют брать $\alpha = 1, \beta = 0,5 \; \text{и} \; \gamma = 2$ . Рекомендация основана на результатах экспериментов с различными комбинациями значений. Эти значения параметров позволяют методу быть эффективным, но работать в различных сложных ситуациях.