Лекция 10: Многометрическая (многомерная) оптимизация. Методы многомерной оптимизации: метод Хука – Дживса, метод Нелдера – Мида, метод полного перебора, метод покоординатного спуска, метод градиентного спуска
До сих пор мы обсуждали одномерные задачи оптимизации, в которых целевая функция зависела только от одного аргумента. Однако подавляющее число реальных задач оптимизации, представляющих практический интерес, являются многомерными: в них целевая функция зависит от нескольких аргументов, причем иногда их число может быть весьма большим.
Математическая постановка таких задач аналогична их постановке в одномерном случае: ищется наименьшее (наибольшее) значение целевой функции, заданной на некотором множестве G возможных значений ее аргументов.
Как и в одномерном случае, характер задачи и соответственно возможные методы решения существенно зависят от той информации о целевой функции, которая нам доступна в процессе ее исследования. В одних случаях целевая функция задается аналитической формулой, являясь при этом дифференцируемой функцией. Тогда можно вычислить ее частные производные, получить явное выражение для градиента, определяющего в каждой точке направления возрастания и убывания функции, и использовать эту информацию для решения задачи. В других случаях никакой формулы для целевой функции нет, а имеется лишь возможность определить ее значение в любой точке рассматриваемой области (с помощью расчетов, в результате эксперимента и т.д.). В таких задачах в процессе решения мы фактически можем найти значения целевой функции лишь в конечном числе точек, и по этой информации требуется приближенно установить ее наименьшее значение для всей области.
1. Метод Хука – Дживса
Этот метод был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха следует поиск по образцу.
Описание этой процедуры представлено ниже:
А. Выбрать начальную базисную точку b1 и шаг длиной hj для каждой переменной xj, j = 1, 2, ..., n. В приведенной ниже программе для каждой переменной используется шаг h, однако указанная выше модификация тоже может оказаться полезной.
Б. Вычислить f(x) в базисной точке b1 с целью получения сведений о локальном поведении функции f(x). Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции. Функция f(x) в базисной точке b1 находится следующим образом:
1. Вычисляется значение функции f(b1) в базисной точке b1.
2. Каждая переменная по очереди изменяется прибавлением длины шага.
Таким образом, мы вычисляем значение функции f(b1 + h1e1), где e1 - единичный вектор в направлении оси х1. Если это приводит к уменьшению значения функции, то b1 заменяется на b1 + h1e1. В противном случае вычисляется значение функции f(b1 – h1e1), и если ее значение уменьшилось, то b1 заменяем на b1-h1e1. Если ни один из проделанных шагов не приводит к уменьшению значения функции, то точка b1 остается неизменной и рассматриваются изменения в направлении оси х2, т.е. находится значение функции f(b1 + h2e2) и т.д. Когда будут рассмотрены все n переменные, мы будем иметь новую базисную точку b2.
3. Если b2 = b1, т.е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b1, но с уменьшенной длиной шага. На практике удовлетворительным является уменьшение шага (шагов) в десять раз от начальной длины.
4. Если  , то производится поиск
по образцу.
, то производится поиск
по образцу.
В. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом:
1. Разумно двигаться из базисной точки b1 в направлении b2 - b1, поскольку поиск в этом направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию в точке образца
 |
( 1.1) |
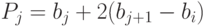 |
( 1.2) |
2. Затем исследование следует продолжать вокруг точки P1 ( Pj ).
3. Если наименьшее значение на шаге В,2 меньше значения в базисной точке b2 (в общем случае bj+1 ), то получают новую базисную точку b3 (bj+2), после чего следует повторить шаг В,1. В противном случае не производить поиск по образцу из точки b2 (bj+1) а продолжить исследования в точке b2 (bj+1).
Г. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена до заданного малого значения.
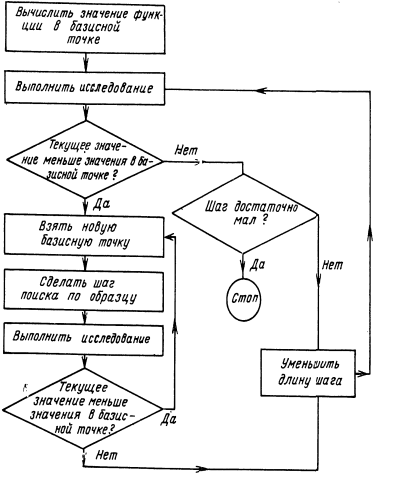
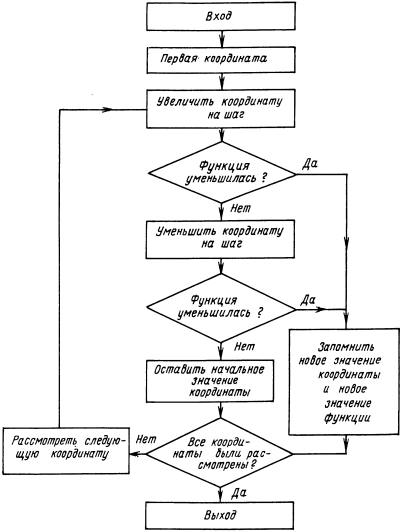
Ниже приведена блок-схема данного метода.