|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Поиск в ширину
BFS-дерево и вычисление расстояний
Другая простая задача, для решения которой можно применить поиск в ширину, - построение каркаса. Напомним, что каркасом графа называется остовный лес, у которого области связности совпадают с областями связности графа. Каркас связного графа - остовное дерево.
Ребра, исследуемые в процессе обхода графа, можно разделить на две
категории: если ребро соединяет активную вершину  с новой
вершиной
с новой
вершиной  , то оно классифицируется как прямое,
в противном случае - как обратное. В зависимости от решаемой задачи
прямые и обратные ребра могут подвергаться различной обработке.
, то оно классифицируется как прямое,
в противном случае - как обратное. В зависимости от решаемой задачи
прямые и обратные ребра могут подвергаться различной обработке.
Предположим, что алгоритм поиска в ширину применяется к связному графу.
Покажем, что в этом случае по окончании обхода множество всех прямых ребер
образует дерево. Действительно, допустим, что на некотором шаге работы
алгоритма обнаруживается новое прямое ребро  , а множество
прямых
ребер, накопленных к этому шагу, образует дерево
, а множество
прямых
ребер, накопленных к этому шагу, образует дерево  .
Тогда вершина
.
Тогда вершина  принадлежит дереву
принадлежит дереву  ,
а вершина
,
а вершина  не принадлежит
ему. Поэтому при добавлении к дереву
не принадлежит
ему. Поэтому при добавлении к дереву  ребра
ребра  связность сохранится, а циклов не появится.
связность сохранится, а циклов не появится.
Итак, если применить поиск в ширину к связному графу и запомнить все прямые ребра, то получим каркас графа. Для произвольного графа будет получен лес, также, очевидно, являющийся каркасом.
Каркас, который будет построен описанным образом в результате поиска в
ширину в связном графе, называется BFS-деревом. Его можно
рассматривать как корневое дерево с корнем в стартовой вершине  .
BFS-дерево с заданным корнем
.
BFS-дерево с заданным корнем  , вообще говоря, не единственное
-
зависит от того, в каком порядке просматриваются окрестности вершин.
Однако всякое BFS-дерево обладает свойством, на котором и основаны
наиболее важные применения поиска в ширину. Каркас
, вообще говоря, не единственное
-
зависит от того, в каком порядке просматриваются окрестности вершин.
Однако всякое BFS-дерево обладает свойством, на котором и основаны
наиболее важные применения поиска в ширину. Каркас  связного
графа
связного
графа  с корнем
с корнем  назовем геодезическим
деревом, если для любой вершины
назовем геодезическим
деревом, если для любой вершины  путь
из
путь
из  в
в  в дереве
в дереве  является кратчайшим путем
между
является кратчайшим путем
между  и
и  в графе
в графе  .
.
Теорема 1. Любое BFS-дерево является геодезическим деревом.
Доказательство. Обозначим через  множество всех вершин
графа, находящихся на расстоянии
множество всех вершин
графа, находящихся на расстоянии  от стартовой
вершины
от стартовой
вершины  .
Работа алгоритма начинается с посещения стартовой вершины,
т.е. единственной вершины, составляющей множество
.
Работа алгоритма начинается с посещения стартовой вершины,
т.е. единственной вершины, составляющей множество  . При
первом
выполнении цикла while будут
посещены и помещены в очередь все
вершины из множества
. При
первом
выполнении цикла while будут
посещены и помещены в очередь все
вершины из множества  . Затем эти вершины будут одна за
другой
извлекаться из очереди, становиться активными, и для каждой из них будут
исследоваться все смежные вершины. Те из них, которые еще не посещались,
будут посещены и помещены в очередь. Но это как раз все вершины из
множества
. Затем эти вершины будут одна за
другой
извлекаться из очереди, становиться активными, и для каждой из них будут
исследоваться все смежные вершины. Те из них, которые еще не посещались,
будут посещены и помещены в очередь. Но это как раз все вершины из
множества  (когда начинается исследование окрестностей
вершин из
(когда начинается исследование окрестностей
вершин из  , ни одна вершина из
, ни одна вершина из  еще не посещалась и
каждая из них
смежна хотя бы с одной вершиной из
еще не посещалась и
каждая из них
смежна хотя бы с одной вершиной из  ). Следовательно, каждая
вершина из
). Следовательно, каждая
вершина из  будет посещена после всех вершин
из
будет посещена после всех вершин
из  .
Рассуждая далее таким образом, приходим к следующему выводу.
.
Рассуждая далее таким образом, приходим к следующему выводу.
(А) Все вершины из 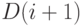 будут посещены после всех вершин
из
будут посещены после всех вершин
из  ,
,  .
.
Строгое доказательство легко провести индукцией по  . Отметим еще
следующий факт.
. Отметим еще
следующий факт.
(Б) Если активной является вершина из  , то в этот момент все
вершины из
, то в этот момент все
вершины из  уже посещены.
уже посещены.
В самом деле, из (А) следует, что вершины из  попадут в
очередь
после вершин из
попадут в
очередь
после вершин из  . Поэтому, когда первая вершина
из
. Поэтому, когда первая вершина
из  становится активной, все вершины из
становится активной, все вершины из  уже закрыты. Значит,
к этому моменту окрестности всех вершин из
уже закрыты. Значит,
к этому моменту окрестности всех вершин из  полностью
исследованы, и, следовательно, все вершины из
полностью
исследованы, и, следовательно, все вершины из  посещены.
посещены.
Рассмотрим теперь момент работы алгоритма, когда активной является вершина  и обнаруживается смежная с ней новая вершина
и обнаруживается смежная с ней новая вершина  .
В BFS-дереве расстояние между
.
В BFS-дереве расстояние между  и
и  на 1 больше, чем
расстояние между
на 1 больше, чем
расстояние между  и
и  . В графе расстояние
между
. В графе расстояние
между  и
и  не больше, чем
не больше, чем  , так как
, так как  и
и  смежны.
Ввиду (А) это расстояние не может быть меньше
смежны.
Ввиду (А) это расстояние не может быть меньше  ,
а ввиду (Б) оно не может быть равно
,
а ввиду (Б) оно не может быть равно  .
Значит,
.
Значит,  , т.е. в графе расстояние
между
, т.е. в графе расстояние
между  и
и  тоже на 1
больше, чем расстояние между
тоже на 1
больше, чем расстояние между  и
и  . Следовательно,
если до какого-то момента работы алгоритма расстояния от каждой из
посещенных вершин до стартовой вершины в графе и в дереве были равны, то
это будет верно и для вновь посещаемой вершины. Поскольку это верно
вначале, когда имеется единственная посещенная вершина
. Следовательно,
если до какого-то момента работы алгоритма расстояния от каждой из
посещенных вершин до стартовой вершины в графе и в дереве были равны, то
это будет верно и для вновь посещаемой вершины. Поскольку это верно
вначале, когда имеется единственная посещенная вершина  (оба
расстояния равны
(оба
расстояния равны  ), то это останется верным и тогда, когда будут
посещены
все вершины.
), то это останется верным и тогда, когда будут
посещены
все вершины.
Итак, мы можем применить поиск в ширину для вычисления расстояний от
стартовой вершины  до всех остальных вершин графа - нужно
только в процессе обхода для каждой посещаемой вершины
до всех остальных вершин графа - нужно
только в процессе обхода для каждой посещаемой вершины  определять расстояние от
определять расстояние от  до
до  в BFS-дереве. Это
сделать
легко:
в BFS-дереве. Это
сделать
легко: 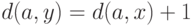 , где
, где  - активная
вершина.
Вначале устанавливаем
- активная
вершина.
Вначале устанавливаем  .
.
Если граф несвязен, некоторые расстояния будут бесконечными. Чтобы учесть
эту возможность, положим вначале  для всех
для всех  .
Пока вершина
.
Пока вершина  остается новой, для нее сохраняется значение
остается новой, для нее сохраняется значение  , когда же она посещается,
, когда же она посещается,  становится равным
расстоянию между
становится равным
расстоянию между  и
и  и больше не меняется. Таким
образом, бесконечность расстояния можно использовать как признак того, что
вершина новая. Если по окончании работы
и больше не меняется. Таким
образом, бесконечность расстояния можно использовать как признак того, что
вершина новая. Если по окончании работы  для
некоторой вершины
для
некоторой вершины  , это означает, что
, это означает, что  не
достижима
из
не
достижима
из  , то есть принадлежит другой компоненте связности.
, то есть принадлежит другой компоненте связности.
Для того чтобы не только определять расстояния, но и находить кратчайшие
пути от  до остальных вершин, достаточно для каждой
вершины
до остальных вершин, достаточно для каждой
вершины  знать ее отца
знать ее отца  в BFS-дереве.
Очевидно, что
в BFS-дереве.
Очевидно, что  ,
где
,
где  - вершина, активная в момент посещения
вершины
- вершина, активная в момент посещения
вершины  .
Заполнение таблицы
.
Заполнение таблицы  фактически означает построение
BFS-дерева.
фактически означает построение
BFS-дерева.
Модифицируя процедуру BFS с учетом сделанных замечаний, получаем следующий алгоритм:
Алгоритм 2. Построение BFS-дерева и вычисление
расстояний от вершины  до всех остальных вершин:
до всех остальных вершин:
-
for
 do
do 

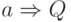
-
while
 do
do

-
for
 do
do
-
if

-
then



