|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Лекция 9: Независимые множества, клики, вершинные покрытия.
Независимые множества, клики, вершинные покрытия
Во многих задачах на графах требуется найти какой-нибудь максимум или минимум, например, наибольший подграф с заданным свойством, или разбиение графа на наименьшее число частей, удовлетворяющих каким-то условиям, и т.д. В оставшихся лекциях рассматриваются несколько задач такого рода, считающихся классическими в теории графов. Некоторые из них известны как NP-трудные, для них рассматриваются переборные алгоритмы, приемы рационализации, эвристики и приближенные алгоритмы. Для других задач излагаются известные эффективные алгоритмы.
Три задачи
Независимым
множеством вершин графа называется любое множество
попарно не смежных вершин, т.е. множество вершин, порождающее пустой
подграф. Независимое множество называется максимальным, если оно не
является собственным подмножеством другого независимого множества,
и наибольшим, если оно
содержит наибольшее количество вершин. Число
вершин в наибольшем независимом множестве графа  обозначается
через
обозначается
через  и называется числом независимости графа.
Задача о независимом множестве состоит в нахождении наибольшего
независимого множества.
и называется числом независимости графа.
Задача о независимом множестве состоит в нахождении наибольшего
независимого множества.
Кликой графа называется множество
вершин, порождающее полный
подграф, т.е. множество вершин, каждые две из которых смежны. Число вершин
в клике наибольшего размера называется кликовым числом графа и
обозначается через  . Очевидно, задача о независимом
множестве преобразуется в задачу о клике и наоборот простым переходом от
данного графа
. Очевидно, задача о независимом
множестве преобразуется в задачу о клике и наоборот простым переходом от
данного графа  к дополнительному графу
к дополнительному графу  , так что
, так что  .
.
Вершинное покрытие
графа - это такое множество вершин, что каждое
ребро графа инцидентно хотя бы одной из этих вершин. Наименьшее число
вершин в вершинном покрытии графа  обозначается через
обозначается через  и называется числом вершинного покрытия графа. В графе на
рис. 9.1 наибольшим независимым множеством является
множество
и называется числом вершинного покрытия графа. В графе на
рис. 9.1 наибольшим независимым множеством является
множество  , наибольшей кликой -
множество
, наибольшей кликой -
множество  , наименьшим вершинным
покрытием - множество
, наименьшим вершинным
покрытием - множество 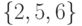 .
.
Между задачами о независимом множестве и о вершинном покрытии тоже имеется простая связь благодаря следующему факту.
Теорема 1. Подмножество  множества вершин графа
множества вершин графа  является вершинным
покрытием тогда и только тогда, когда
является вершинным
покрытием тогда и только тогда, когда 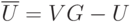 - независимое
множество.
- независимое
множество.
Доказательство. Если  - вершинное покрытие, то всякое
ребро содержит хотя бы одну вершину из множества
- вершинное покрытие, то всякое
ребро содержит хотя бы одну вершину из множества  и, значит,
нет
ни одного ребра, соединяющего две вершины из множества
и, значит,
нет
ни одного ребра, соединяющего две вершины из множества  .
Следовательно,
.
Следовательно,  - независимое множество. Обратно,
если
- независимое множество. Обратно,
если  - независимое множество, то нет ребер, соединяющих
вершины из
- независимое множество, то нет ребер, соединяющих
вершины из  и, значит, у каждого ребра одна или обе вершины
принадлежат
множеству
и, значит, у каждого ребра одна или обе вершины
принадлежат
множеству  . Следовательно,
. Следовательно,  - вершинное
покрытие.
- вершинное
покрытие.
Из этой теоремы следует, что  для
любого
графа
для
любого
графа  с
с  вершинами.
вершинами.
Таким образом, все три задачи тесно связаны друг с другом, так что достаточно научиться решать одну из них, и мы будем уметь решать остальные две. Вместе с тем известно, что эти задачи NP-полны. Для таких задач не известно эффективных алгоритмов, а накопленный к настоящему времени опыт делает правдоподобным предположение о том, что таких алгоритмов и не существует. Тем не менее, алгоритмы для подобных задач разрабатывались и продолжают разрабатываться, и в некоторых случаях они могут быть полезны. Все эти алгоритмы в той или иной форме осуществляют перебор вариантов (число которых может быть очень большим). Далее рассмотрим один из способов такого перебора для задачи о независимом множестве.

