|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Поиск в ширину
Поиск в ширину
С этой лекции мы начинаем рассматривать алгоритмы для решения различных задач на графах. Сначала речь пойдет о задачах анализа графов с целью выявления их структуры и вычисления метрических характеристик. Многие задачи такого рода могут быть решены путем систематического обхода графа с посещением всех его вершин и исследованием всех его ребер. Такой обход можно выполнить многими способами, в действительности же широкое распространение благодаря своей простоте, а в большей степени своей полезности, получили две стратегии - поиск в глубину и поиск в ширину. Рассмотрение этих алгоритмов и примеров их применения к задачам анализа графов составляет содержание этой и двух следующих лекций.
Процедура поиска в ширину
Работа всякого алгоритма обхода состоит в последовательном посещении вершин и исследовании ребер. Какие именно действия выполняются при посещении вершины и исследовании ребра - зависит от конкретной задачи, для решения которой производится обход. В любом случае, однако, факт посещения вершины запоминается, так что с момента посещения и до конца работы алгоритма она считается посещенной. Вершину, которая еще не посещена, будем называть новой. В результате посещения вершина становится открытой и остается такой, пока не будут исследованы все инцидентные ей ребра. После этого она превращается в закрытую.
Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их
удаленности от некоторой заранее выбранной или указанной стартовой
вершины  . Иначе говоря, сначала посещается
сама вершина
. Иначе говоря, сначала посещается
сама вершина  , затем все
вершины, смежные с
, затем все
вершины, смежные с  , то есть находящиеся от нее на
расстоянии
, то есть находящиеся от нее на
расстоянии  ,
затем вершины, находящиеся от
,
затем вершины, находящиеся от  на расстоянии
на расстоянии 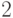 , и
т.д.
, и
т.д.
Рассмотрим алгоритм поиска в ширину с заданной стартовой
вершиной  .
Вначале все вершины помечаются как новые. Первой посещается
вершина
.
Вначале все вершины помечаются как новые. Первой посещается
вершина  , она становится единственной открытой вершиной.
В дальнейшем каждый очередной шаг начинается с выбора некоторой открытой
вершины
, она становится единственной открытой вершиной.
В дальнейшем каждый очередной шаг начинается с выбора некоторой открытой
вершины  . Эта вершина становится активной. Далее исследуются ребра, инцидентные активной вершине. Если такое ребро соединяет вершину
. Эта вершина становится активной. Далее исследуются ребра, инцидентные активной вершине. Если такое ребро соединяет вершину  с новой вершиной
с новой вершиной  , то вершина
, то вершина  посещается и превращается
в открытую. Когда все ребра, инцидентные активной вершине, исследованы,
она перестает быть активной и становится закрытой. После этого выбирается
новая активная вершина, и описанные действия повторяются. Процесс
заканчивается, когда множество открытых вершин становится пустым.
посещается и превращается
в открытую. Когда все ребра, инцидентные активной вершине, исследованы,
она перестает быть активной и становится закрытой. После этого выбирается
новая активная вершина, и описанные действия повторяются. Процесс
заканчивается, когда множество открытых вершин становится пустым.
Основная особенность поиска в ширину, отличающая его от других способов обхода графов, состоит в том, что в качестве активной вершины выбирается та из открытых, которая была посещена раньше других. Именно этим обеспечивается главное свойство поиска в ширину: чем ближе вершина к старту, тем раньше она будет посещена. Для реализации такого правила выбора активной вершины удобно использовать для хранения множества открытых вершин очередь - когда новая вершина становится открытой, она добавляется в конец очереди, а активная выбирается в ее начале. Схематически процесс изменения статуса вершин изображен на рис. 4.1. Черным кружком обозначена активная вершина.
Опишем процедуру поиска в ширину (BFS - от английского названия этого
алгоритма - Breadth First Search) из заданной стартовой вершины  .
В этом описании
.
В этом описании  обозначает множество всех вершин, смежных
с вершиной
обозначает множество всех вершин, смежных
с вершиной  ,
,  - очередь открытых вершин.
Предполагается, что при посещении вершины она помечается как посещенная
и эта пометка означает, что вершина уже не является новой.
- очередь открытых вершин.
Предполагается, что при посещении вершины она помечается как посещенная
и эта пометка означает, что вершина уже не является новой.
Procedure BFS(a)
- посетить вершину

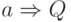
-
while
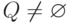 do
do

-
for
 do
do
- исследовать ребро

-
if вершина
 новая
новая -
then посетить
вершину


Отметим некоторые свойства процедуры BFS.
-
Процедура BFS заканчивает работу после конечного
числа шагов.
Действительно, при каждом повторении цикла while из очереди удаляется одна вершина. Вершина добавляется к очереди только тогда, когда она посещается. Каждая вершина может быть посещена не более одного раза, так как посещаются только новые вершины, а в результате посещения вершина перестает быть новой. Таким образом, число повторений цикла while не превосходит числа вершин.
-
В результате выполнения процедуры BFS будут посещены
все вершины из компоненты связности, содержащей вершину a,
и только они.
Очевидно, что вершина может быть посещена только в том случае, когда существует путь, соединяющий ее с вершиной
 (так как посещается
всегда вершина, смежная с уже посещенной). То, что каждая такая вершина
будет посещена, легко доказывается индукцией по расстоянию от данной
вершины до вершины
(так как посещается
всегда вершина, смежная с уже посещенной). То, что каждая такая вершина
будет посещена, легко доказывается индукцией по расстоянию от данной
вершины до вершины  .
. -
Время работы процедуры BFS есть
 , где
, где  -
число ребер в компоненте связности, содержащей вершину
-
число ребер в компоненте связности, содержащей вершину  .
.
Из предыдущих рассуждений видно, что каждая вершина из этой компоненты
становится активной точно один раз. Внутренний цикл for для
активной вершины  выполняется
выполняется  раз.
Следовательно,
общее число повторений внутреннего цикла будет равно
раз.
Следовательно,
общее число повторений внутреннего цикла будет равно  .
.
Итак, процедура BFS(  ) производит обход компоненты связности,
содержащей вершину
) производит обход компоненты связности,
содержащей вершину  . Чтобы перейти к другой компоненте,
достаточно
выбрать какую-нибудь новую вершину (если такие вершины еще имеются),
в качестве стартовой. Пусть
. Чтобы перейти к другой компоненте,
достаточно
выбрать какую-нибудь новую вершину (если такие вершины еще имеются),
в качестве стартовой. Пусть 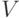 - множество вершин графа.
Следующий
алгоритм осуществляет полный обход графа методом поиска в ширину.
- множество вершин графа.
Следующий
алгоритм осуществляет полный обход графа методом поиска в ширину.
Алгоритм 1. Поиск в ширину.
Учитывая, что цикл for в
строке  повторяется
повторяется  раз,
где
раз,
где  - число вершин графа, получаем общую оценку
трудоемкости
- число вершин графа, получаем общую оценку
трудоемкости  . Необходимо отметить, что эта оценка
справедлива
в предположении, что время, требуемое для просмотра окрестности вершины,
пропорционально степени этой вершины. Это имеет место, например, если граф
задан списками смежности. Если же граф задан матрицей смежности, то для
просмотра окрестности любой вершины будет затрачиваться время,
пропорциональное
. Необходимо отметить, что эта оценка
справедлива
в предположении, что время, требуемое для просмотра окрестности вершины,
пропорционально степени этой вершины. Это имеет место, например, если граф
задан списками смежности. Если же граф задан матрицей смежности, то для
просмотра окрестности любой вершины будет затрачиваться время,
пропорциональное  . В этом случае общее время работы
алгоритма будет оцениваться как
. В этом случае общее время работы
алгоритма будет оцениваться как  . Наибольшее значение
величины
. Наибольшее значение
величины  при данном
при данном  равно
равно  , т.е.
имеет порядок
, т.е.
имеет порядок  . Таким образом, трудоемкость алгоритма поиска
в ширину при задании графа списками смежности не выше, чем при задании
матрицей смежности. В целом же первый способ задания предпочтительнее, так
как дает выигрыш для графов с небольшим числом ребер.
. Таким образом, трудоемкость алгоритма поиска
в ширину при задании графа списками смежности не выше, чем при задании
матрицей смежности. В целом же первый способ задания предпочтительнее, так
как дает выигрыш для графов с небольшим числом ребер.
В качестве простейшего примера применения поиска в ширину для графа
рассмотрим задачу выявления компонент связности. Допустим, мы хотим
получить ответ в виде таблицы, в которой для каждой вершины  указан номер
указан номер  компоненты, которой принадлежит эта
вершина.
Компоненты будут получать номера в процессе обхода. Для решения этой
задачи достаточно ввести переменную
компоненты, которой принадлежит эта
вершина.
Компоненты будут получать номера в процессе обхода. Для решения этой
задачи достаточно ввести переменную  со значением, равным
текущему номеру компоненты, и каждый раз при посещении новой
вершины
со значением, равным
текущему номеру компоненты, и каждый раз при посещении новой
вершины  полагать
полагать  . Значение
. Значение  первоначально
устанавливается равным
первоначально
устанавливается равным  и модифицируется при каждом вызове
процедуры BFS.
и модифицируется при каждом вызове
процедуры BFS.


 do if
do if