|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Жадные алгоритмы и матроиды
Жадные алгоритмы и матроиды
Жадными (градиентными) называют алгоритмы, действующие по принципу "максимальный выигрыш на каждом шаге". Такая стратегия не всегда ведет к конечному успеху - иногда выгоднее сделать не наилучший, казалось бы, выбор на очередном шаге с тем, чтобы в итоге получить оптимальное решение. Но для некоторых задач применение жадных алгоритмов оказывается оправданным. Одной из самых известных задач такого рода является задача об оптимальном каркасе. Существует общая теория, обосновывающая применимость жадных алгоритмов к задачам определенного типа, к которому относится и рассмотренный в "предыдущей лекции" алгоритм Крускала. В этой лекции будет дан набросок этой теории. Затем будет рассмотрено применение жадного алгоритма в сочетании с методом увеличивающих путей для решения задачи о паросочетании наибольшего веса в двудольном графе со взвешенными вершинами.
Матроиды
Когда возник вопрос о том, каковы обстоятельства, при которых жадный алгоритм результативен, или иначе - что особенного в тех задачах, для которых он дает точное решение, оказалось, что математическая теория, с помощью которой что-то в этом можно прояснить, уже существует. Это теория матроидов, основы которой были заложены Уитни в работе 1935 г. Целью создания теории матроидов было изучение комбинаторного аспекта линейной независимости, а в дальнейшем обнаружились разнообразные применения понятия матроида, первоначально совсем не имевшиеся в виду.
Определение. Матроидом называется
пара  , где
, где  -
конечное непустое множество,
-
конечное непустое множество,  - семейство
подмножеств множества
- семейство
подмножеств множества  , удовлетворяющее условиям:
, удовлетворяющее условиям:
- (1) если
 и
и  ,
то
,
то  ;
; - (2) если
 ,
,  и
и  , то существует
такой элемент
, то существует
такой элемент 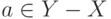 , что
, что  .
.
Элементы множества  называются элементами матроида,
а множества из семейства
называются элементами матроида,
а множества из семейства  - независимыми множествами
матроида. Максимальное по включению независимое множество называют базой матроида. Из аксиомы (2)
следует,
что все базы матроида состоят из одинакового количества элементов.
- независимыми множествами
матроида. Максимальное по включению независимое множество называют базой матроида. Из аксиомы (2)
следует,
что все базы матроида состоят из одинакового количества элементов.
Если  - множество строк некоторой матрицы,
а
- множество строк некоторой матрицы,
а  состоит
из всех линейно независимых множеств строк этой матрицы,
то пара
состоит
из всех линейно независимых множеств строк этой матрицы,
то пара  образует матроид,
называемый матричным
матроидом.
образует матроид,
называемый матричным
матроидом.
Другим важным типом матроидов являются графовые матроиды. Пусть 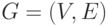 - обыкновенный граф. Подмножество множества
- обыкновенный граф. Подмножество множества  назовем ациклическим, если подграф,
образованный ребрами этого подмножества,
не содержит циклов, т.е. является лесом.
назовем ациклическим, если подграф,
образованный ребрами этого подмножества,
не содержит циклов, т.е. является лесом.
Теорема 1. Если 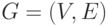 - обыкновенный граф,
- обыкновенный граф,  - семейство всех ациклических подмножеств
множества
- семейство всех ациклических подмножеств
множества  , то
пара
, то
пара  является матроидом.
является матроидом.
Доказательство. Аксиома (1) выполняется, так как всякое
подмножество ациклического множества, очевидно, является ациклическим.
Докажем, что выполняется и (2). Пусть  и
и  -
два
ациклических множества и
-
два
ациклических множества и  . Допустим, что не существует
такого
ребра
. Допустим, что не существует
такого
ребра  , что множество
, что множество  является
ациклическим. Тогда при добавлении любого ребра из множества
является
ациклическим. Тогда при добавлении любого ребра из множества  к множеству
к множеству  образуется цикл. Это означает, что концы каждого
такого ребра принадлежат одной компоненте связности остовного подграфа,
образованного ребрами множества
образуется цикл. Это означает, что концы каждого
такого ребра принадлежат одной компоненте связности остовного подграфа,
образованного ребрами множества  . Тогда каждая область связности
подграфа
. Тогда каждая область связности
подграфа  содержится в какой-нибудь области связности
подграфа
содержится в какой-нибудь области связности
подграфа  .
Но компоненты связности каждого из этих подграфов - деревья,
а дерево с
.
Но компоненты связности каждого из этих подграфов - деревья,
а дерево с  вершинами содержит ровно
вершинами содержит ровно  ребер.
Следовательно, в этом случае число ребер в
ребер.
Следовательно, в этом случае число ребер в  не превосходило бы
числа ребер в
не превосходило бы
числа ребер в  , что противоречит
условию
, что противоречит
условию  .
.
Базами графового матроида являются все каркасы графа. Для связного графа это будут все его остовные деревья.
