|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Введение в машинное обучение
Презентацию к лекции Вы можете скачать здесь.
1. Введение в машинное обучение
Машинное обучение (machine learning) – это область научного знания, имеющая дело с алгоритмами, "способными обучаться". Необходимость использования методов машинного обучения объясняется тем, что для многих сложных – "интеллектуальных" – задач (например, распознавание рукописного текста, речи и т. п.) очень сложно (или даже невозможно) разработать "явный" алгоритм их решения, однако часто можно научить компьютер обучиться решению этих задач. Одним из первых, кто использовал термин "машинное обучение", был изобретатель первой самообучающейся компьютерной программы игры в шашки А. Л. Самуэль в 1959 г. [ 10 ]. Под обучением он понимал процесс, в результате которого компьютер способен показать поведение, которое в нее не было заложено "явно". Это определение не выдерживает критики, так как не понятно, что означает наречие "явно". Более точное определение дал намного позже Т. М. Митчелл [ 9 ]: говорят, что компьютерная программа обучается на основе опыта E по отношению к некоторому классу задач T и меры качества P, если качество решения задач из T, измеренное на основе P, улучшается с приобретением опыта E.
Заметим, что фаза обучения может предшествовать фазе работы алгоритма (например, детектирование лиц на фотокамере), но может иметь место обратная ситуация: обучение (и дополнительное обучение) может проходить в процессе функционирования самого алгоритма (например, определение спама).
В настоящее время машинное обучение имеет многочисленные сферы приложения, такие, как компьютерное зрение, распознавание речи, компьютерная лингвистика и обработка естественных языков, медицинская диагностика, биоинформатика, техническая диагностика, финансовые приложения, поиск и рубрикация текстов, интеллектуальные игры, экспертные системы и др.
Различают дедуктивное и индуктивное обучение. В задачах дедуктивного обучения имеются знания, каким-либо образом формализованные. Требуется вывести из них правило, применительное к конкретному случаю. Дедуктивное обучение относят к области экспертных систем и здесь рассматриваться не будет. Основная задача индуктивного обучения заключается в восстановлении некоторой зависимости по эмпирическим данным. Индуктивное обучение подразделяется на обучение с учителем, обучение без учителя, обучение с подкреплением (reinforcement learning), активное обучение и др.
Обстоятельными учебниками по машинному обучению являются [ 1 , 8 , 9 ] и др. Также рекомендуем русскоязычный ресурс www.machinelearning.ru и сайт курса по машинному обучению одного из авторов настоящего пособия www.uic.unn.ru/~zny/ml.
1.1. Задача обучения с учителем
1.1.1. Постановка задачи обучения с учителем
Рассмотрим постановку задачи обучения с учителем (supervised learning). Пусть  - некоторое множество, элементы которого называются объектами или примерами, ситуациями, входами (samples); а
- некоторое множество, элементы которого называются объектами или примерами, ситуациями, входами (samples); а  - множество, элементы которого называются
- множество, элементы которого называются  или откликами, метками, выходами (responses). Имеется некоторая зависимость (детерминированная или вероятностная), позволяющая по
или откликами, метками, выходами (responses). Имеется некоторая зависимость (детерминированная или вероятностная), позволяющая по  предсказать
предсказать 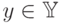 . В частности, если зависимость детерминированная, то существует функция
. В частности, если зависимость детерминированная, то существует функция  . Зависимость известна только на объектах обучающей выборки
. Зависимость известна только на объектах обучающей выборки
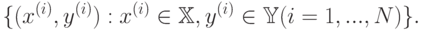
Упорядоченная пара "объект-ответ" 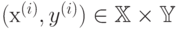 называется прецедентом.
называется прецедентом.
Задача обучения с учителем заключается в восстановлении зависимости между входом и выходом по имеющейся обучающей выборке, т. е. необходимо построить функцию (решающее правило)  , по новым объектам
, по новым объектам  предсказывающую ответ
предсказывающую ответ 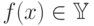 :
:

Функция  при этом выбирается из некоторого множества возможных моделей
при этом выбирается из некоторого множества возможных моделей 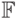 . Процесс нахождения
. Процесс нахождения  называется обучением (learning), а также настройкой или подгонкой (fitting) модели.
называется обучением (learning), а также настройкой или подгонкой (fitting) модели.
Алгоритм построения функции  по заданной обучающей выборке называется алгоритмом обучения. Некоторый класс алгоритмов называется методом обучения. Иногда термины "алгоритм" и "метод" используются как синонимы.
по заданной обучающей выборке называется алгоритмом обучения. Некоторый класс алгоритмов называется методом обучения. Иногда термины "алгоритм" и "метод" используются как синонимы.
Алгоритмы обучения, конечно же, оперируют не с самими объектами, а их описаниями. Наиболее распространенным является признаковое описание. При таком подходе объект  представляется как вектор
представляется как вектор 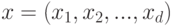 , где
, где  . Таким образом,
. Таким образом,

Компонента  называется j-м признаком, или свойством (feature), или атрибутом объекта
называется j-м признаком, или свойством (feature), или атрибутом объекта  . Если
. Если 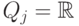 , то j-й признак называется количественным или вещественным. Если
, то j-й признак называется количественным или вещественным. Если  конечно, то j-й признак называется номинальным, или категориальным, или фактором. Если при этом
конечно, то j-й признак называется номинальным, или категориальным, или фактором. Если при этом 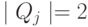 , то признак называется бинарным. Если
, то признак называется бинарным. Если  конечно и упорядочено, то признак называется порядковым. Множество
конечно и упорядочено, то признак называется порядковым. Множество  называется пространством признаков.
называется пространством признаков.
В зависимости от того, какие значения может принимать ответ  , различают разные классы задач обучения с учителем. Если
, различают разные классы задач обучения с учителем. Если  , то говорят о задаче восстановления регрессии. Решающее правило
, то говорят о задаче восстановления регрессии. Решающее правило  при этом называют регрессией. Если
при этом называют регрессией. Если  конечно, например,
конечно, например,  , то говорят о задаче классификации. Решающее правило
, то говорят о задаче классификации. Решающее правило  при этом называют классификатором. В последнем случае
при этом называют классификатором. В последнем случае  можно интерпретировать как номер класса, к которому принадлежит объект
можно интерпретировать как номер класса, к которому принадлежит объект  . К задачам обучения относят также задачи ранжирования, прогнозирования и др.
. К задачам обучения относят также задачи ранжирования, прогнозирования и др.
Сделаем два замечания, касающиеся качества решения задачи.
Во-первых, найденное решающее правило должно обладать обобщающей способностью. Иными словами, построенный классификатор или функция регрессии должны отражать общую зависимость выхода от входа, основываясь лишь на известных данных о прецедентах обучающей выборки. При решении прикладных задач, как правило, говорить о восстановлении истинной взаимосвязи не приходится, и, следовательно, речь может идти лишь об отыскании некоторой аппроксимации. Таким образом, обученная модель должна выдавать в среднем достаточно точные предсказания на новых (не входящих в обучающую выборку) прецедентах.
Во-вторых, следует уделить внимание проблеме эффективной вычислимости функции  . Аналогичное требование предъявляется и к алгоритму обучения: настройка модели должна происходить за приемлемое время.
. Аналогичное требование предъявляется и к алгоритму обучения: настройка модели должна происходить за приемлемое время.
Пусть для задачи обучения с учителем определена функция потерь, или функцию штрафа,  , представляющая собой неотрицательную функцию от истинного значения выхода
, представляющая собой неотрицательную функцию от истинного значения выхода  и предсказанного с помощью модели значения
и предсказанного с помощью модели значения  . Например, для задачи восстановления регрессии часто используют квадратичный штраф
. Например, для задачи восстановления регрессии часто используют квадратичный штраф
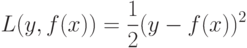
или абсолютный штраф:
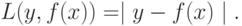
Для задачи классификации можно взять ошибку предсказания

где  - индикаторная функция:
- индикаторная функция:

Математическое ожидание функции потерь

называется средней ошибкой, или средним риском. В качестве решающего правила разумно взять функцию 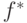 , минимизирующую эту ошибку:
, минимизирующую эту ошибку:
 |
( 1) |
Часто закон распределения совместной случайной величины  не известен, поэтому данный критерий не применим. Вместо среднего риска
не известен, поэтому данный критерий не применим. Вместо среднего риска 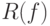 рассмотрим эмпирический риск, или эмпирическую ошибку,
рассмотрим эмпирический риск, или эмпирическую ошибку,

Критерий (1) заменим следующим:
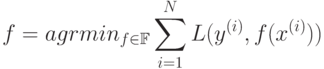 |
( 2) |
где прецеденты  составляют обучающую выборку.
составляют обучающую выборку.
В итоге задача свелась к отысканию функции  из допустимого множества
из допустимого множества 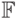 , удовлетворяющей условию (2), при условии, что
, удовлетворяющей условию (2), при условии, что 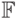 и
и  фиксированы и известны. Это так называемый принцип минимизации эмпирического риска. Как правило, класс
фиксированы и известны. Это так называемый принцип минимизации эмпирического риска. Как правило, класс 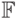 параметризован, т. е. есть имеется его описание в вида
параметризован, т. е. есть имеется его описание в вида  , где
, где  - некоторое известное множество. В процессе настройки модели алгоритмом обучения выбираются значения набора параметров
- некоторое известное множество. В процессе настройки модели алгоритмом обучения выбираются значения набора параметров  , обеспечивающих точное или приближенное выполнение условия (2), т. е. минимизации ошибки на прецедентах обучающей выборки. Однако данное условие не подходит для оценки обобщающей способности алгоритма. Более того, значения
, обеспечивающих точное или приближенное выполнение условия (2), т. е. минимизации ошибки на прецедентах обучающей выборки. Однако данное условие не подходит для оценки обобщающей способности алгоритма. Более того, значения  и
и 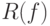 могут различаться значительно. Ситуация, когда
могут различаться значительно. Ситуация, когда  мало, а
мало, а 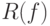 чересчур велико, называется переобучением.
чересчур велико, называется переобучением.
На практике все имеющиеся данные разбивают на обучающую и тестовую выборки. Обучение производится с использованием обучающей выборки, а оценка качества предсказания на основе данных тестовой выборки.
Другим практическим методом оценки обобщающей способности решающего правила является метод  -кратного перекрестного (скользящего) контроля (CV - cross validation). Все имеющиеся данные разбиваются на
-кратного перекрестного (скользящего) контроля (CV - cross validation). Все имеющиеся данные разбиваются на  примерно равных (по числу прецедентов) частей. Далее, отделяя из выборки одну за другой каждую из этих частей, используют оставшиеся данные (составленные из
примерно равных (по числу прецедентов) частей. Далее, отделяя из выборки одну за другой каждую из этих частей, используют оставшиеся данные (составленные из  частей) как обучающую выборку, а отделенную часть - как тестовую. Итоговая оценка ошибки определяется как средняя по всем разбиениям. Заметим, что само итоговое решающее правило строится по всей имеющейся обучающей выборке.
частей) как обучающую выборку, а отделенную часть - как тестовую. Итоговая оценка ошибки определяется как средняя по всем разбиениям. Заметим, что само итоговое решающее правило строится по всей имеющейся обучающей выборке.
Часто используют значения  или 10 . Если
или 10 . Если 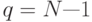 , то говорят о методе скльзящего контроля с одним отделяемым объектом (LOO - leave-one-out estimate).
, то говорят о методе скльзящего контроля с одним отделяемым объектом (LOO - leave-one-out estimate).
1.1.2. Метод k ближайших соседей
Метод k ближайших соседей (k nearest-neighbor, k-NN) относится к наиболее простым и в то же время универсальным методам, используемым как для решения задач классификации, так и восстановления регрессии. В случае классификации новый объект классифицируется путем отнесения его к классу, являющемуся преобладающим среди k ближайших (в пространстве признаков) объектов из обучающей выборки. Если 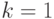 , тоновый объект относится к тому же классу, что и ближайший объект из обучающей выборки.
, тоновый объект относится к тому же классу, что и ближайший объект из обучающей выборки.
Аналогичный способ используется и в задаче восстановления регрессии, с той лишь разницей, что в качестве ответа для объекта выступает среднее ответов k ближайших к нему объектов из обучающей выборки.
Опишем метод более формально. Пусть - множество
- множество  ближайших к
ближайших к  объектов из обучающей выборки. Тогда для задачи классификации положим
объектов из обучающей выборки. Тогда для задачи классификации положим

а для задачи восстановления регрессии -
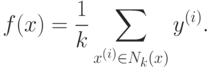
В некоторых случаях данные ответы учитываются с весами, обратно пропорциональными расстоянию до объекта. Это особенно полезно для решения задачи классификации с несбалансированными данными, т. е. когда число объектов, относящихся к разным классам, сильно различно.
Для определения ближайших соседей обычно используется евклидово расстояние

однако оно применимо только для признаков, описываемых количественными переменными. Если все переменные качественные, то можно использовать расстояние Хэмминга

В общем случае используют функцию

где 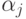 - неотрицательные параметры,
- неотрицательные параметры, 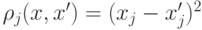 для качественных переменных,
для качественных переменных,  для качественных переменных. Заметим, что функция расстояния не обязательно должна быть метрикой и неравенство треугольника может быть не выполнено.
для качественных переменных. Заметим, что функция расстояния не обязательно должна быть метрикой и неравенство треугольника может быть не выполнено.
Для повышения точности модели также могут использоваться специальные алгоритмы обучения метрики расстояния (например, Large Margin Nearest Neighbour [ 8 ]).
Одним из основных параметров, влияющих на обобщающую способность алгоритма, является число "ближайших соседей"  . В целом, выбор определенного значения обусловлен характером данных задачи. Большие значения
. В целом, выбор определенного значения обусловлен характером данных задачи. Большие значения  могут привести как к более точному описанию границы, разделяющей классы, так и переобучению. Обычно для выбора
могут привести как к более точному описанию границы, разделяющей классы, так и переобучению. Обычно для выбора  применяют различные эвристики, в частности, метод перекрестного контроля.
применяют различные эвристики, в частности, метод перекрестного контроля.

