|
Неоднократно находил ошибки в тестах, особенно в экзаменационных вопросах, когда правильно данный ответ на вопрос определялся в итоге как не правильно отвеченный... Из-за этого сильно страдает конечный бал! Да еще в заблуждение студентов вводит! Они-то думают, что это они виноваты!!! Но они тут не причем! Я много раз проверял ответы на некоторые такие "ошибочные" вопросы по нескольким источникам - результат везде одинаковый! Но ИНТУИТ выдавал ошибку... Как это понимать? Из-за подобных недоразумений приходиться часами перерешивать экзамен на отличную оценку...!!! Исправьте, пожалуйста, такие "ошибки"... |
Новое поколение технологического оборудования
Система управления
Система управления робота-станка (рис. 8.3) построена на базе встроенного персонального компьютера, выполняющего в реальном масштабе времени следующие операции:
- планирование траекторий перемещения манипуляторов на основе данных с чертежа поверхности;
- управление исполнительными приводами;
- обработка информации с датчиков перемещения манипуляторов;
- обработка информации с системы контроля геометрических размеров обрабатываемой поверхности и коррекция траектории перемещения манипуляторов.
Для формирования траектории перемещения инструмента необходимо иметь описание обрабатываемой поверхности. Так, для описания поверхности пера лопаток турбин, задаваемых координатами опорных точек, используются в зависимости от требуемой точности либо сплайн-функции, либо многомерные полиномы [ 9.3 ] . В случае использования полинома второго порядка двух переменных независимо от типа полинома описание приводится к степенному ряду двух переменных
yд=A1zд2xд2+A2zд2xд+A3zдxд2+A4zд2+A5xд2+A6zдxд+A7zд+A8xд+A9, (9.2)
где коэффициенты Ak вычисляются через постоянные коэффициенты описываемого полинома. Полное представление сложной поверхности координатамиопорных точек, а также методика описания поверхности рассмотрены в лекции 11. Для автоматизированного программирования траектории перемещения инструмента по данным с чертежа обрабатываемой поверхности разработана применительно для IBM РС Система Автоматизированного Программирования (САП).
Управление исполнительными приводами в первую очередь состоит в решении обратной задачи о положениях, которая для механизмов относительного манипулирования представляет определение обобщенных координат манипуляторов детали qд и инструмента qи по информации о перемещении инструмента относительно детали (рис. 9.1).
При обработке поверхности программная траектория перемещения инструмента относительно обрабатываемого изделия для каждой i -й точки поверхности задается элементами матрицы [4 x 4]дAi, которая определяет положение режущей кромки инструмента в системе координат (X,Y,Z)д (рис. 9.5).
Для вывода уравнений кинематики и динамики механизмов используется аппарат однородных матриц и матричных преобразований, предложенных Ж.Денавитом и Р.Хартенбергом [ 9.4 ] . Основой данного математического аппарата являются матрицы [4 x 4], описывающие преобразование координат из одной системы (k+1) в другую (k)
где
- подматрица направляющих косинусов, или матрица поворота осей системы координат (XYZ)k+1 относительно осей (XYZ)k ;
kRk+1=[xk+1yk+1zk+1]T - вектор, определяющий положение точки 0k+1 в системе координат XYZk ;
0T - подматрица преобразования перспективы;
1 - глобальный масштабирующий множитель.
Перемещение выходного звена манипулятора определяется положением системы координат (XYZ)д в неподвижной системе координат (XYZ)0, представляемой матрицей [4 x 4]OAд (рис. 9.3). Математически условие обработки поверхности состоит в обеспечении фундаментального матричного уравнения для каждой точки ( i -й) траектории движения инструмента относительно детали
0Ai(qи)=0Aд(qд)дAi,
которое преобразуется к виду
(0Aд(qд))-1*0Ai(qи)=дAi. (9.4)
Приравнивая три элемента 4-го столбца и три элемента, не принадлежащие одной строке и одному столбцу из 1-го, 2-го и 3-го столбца, в левой и правой частях уравнения (9.4), получим систему из шести уравнений
F(qи, qд)=U, (9.5)
которая является исходной системой и ее решение относительно qи и qд должно быть заложено в системе управления. Решение данного трансцендентного уравнения в явном виде определяется видом уравнения. В лекции 10 решение данного уравнения рассмотрено в линейном виде, когда в каждый момент времени рассчитываются приращения обобщенных координат, которые последовательно прибавляются к начальному значению.
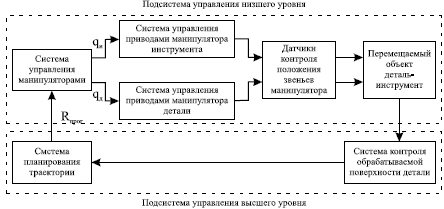
Система оптического контроля геометрии поверхностей сложной формы, разработанная в НПО"Луч", предназначена для определения отклонений параметров обрабатываемой поверхности от заданных и отслеживания ее качества. Блок-схема системы управления робота-станка, включающая систему контроля поверхности, приведена на рисунке 9.6, где система планирования траектории на основе данных чертежа и реальных геометрических размеров обработанной поверхности формирует промежуточные координаты Rпрог.. Система управления манипуляторами на основе Rпрог. формирует управляемые координаты на исполнительные приводы qи и qд и осуществляет управление приводами.
Проектирование технологических машин нового поколения для обработки сложных поверхностей включает следующие основные этапы:
- Выбор кинематической схемы технологической машины на основе функционального назначения манипуляторов, обеспечивающих требуемые перемещения инструмента относительно детали и независимые транспортные перемещения детали и инструмента.
- Проектирование системы управления на базе универсальной ЭВМ, имеющей необходимый объем памяти для планирования траекторий перемещения манипуляторов и обеспечения управления приводами по информации с датчиков положения манипуляторов.
- Синтез управления исполнительными приводами с учетом технологического процесса как элемента системы.
- Разработка программного обеспечения и планирование траекторий перемещения манипуляторов, в целях получения требуемых показателей качества.
Технологические машины, построенные на механизмах относительного манипулирования и оснащенные современными управляющими вычислительными системами, позволяют выполнять механическую обработку деталей со сложными поверхностями, имеют существенно меньшую металлоемкость в сравнении с оборудованием, применяемым в настоящее время для этих целей, позволяют одними и теми же механизмами выполнять транспортные и обрабатывающие операции.