Математические принципы реализации автоматического управления
5.1.2. Пропорциональный регулятор
5.1.1. Описание
При автоматическом регулировании управляющее воздействие 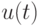 обычно является функцией динамической ошибки - отклонения
обычно является функцией динамической ошибки - отклонения  регулируемой величины
регулируемой величины  от ее заданного значения
от ее заданного значения 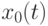 :
:

Это принцип Ползунова-Уатта регулирования по отклонению, или принцип обратной связи. Математическое выражение функциональной зависимости желаемого управляющего воздействия  от измеряемых регулятором величин называется законом или алгоритмом регулирования.
от измеряемых регулятором величин называется законом или алгоритмом регулирования.
Пропорциональный регулятор - это устройство, оказывающее управляющее воздействие на объект пропорционально его линейному отклонению от заданного состояния:

Здесь  - это коэффициент усиления регулятора.
- это коэффициент усиления регулятора.
5.1.2. Управление мотором
Если мы представим, что управляем манипулятором, то первая задача, которая перед нами встаёт - это отработка заданных углов звеньев манипулятора, что бы заданное фиксированное положение. Соответственно надо придумать алгоритм, который задержит мотор, удерживающий звено манипулятора, в строго фиксированном положении. В этом нам снова поможет п-регулятор.
Балку, прикреплённую к мотору можно трактовать как первое звено манипулятора. По сценарию, в момент запуска его надо поднять на 45 градусов и удерживать в этом положении, что бы ни случилось.
Алгоритм таков: обнулить показания датчика оборотов, задать желаемое положение в 45 градусов и в цикле поддерживать это положение, учитывая возможные отклонения.
Пусть 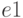 - показания датчика оборотов на моторе А. Тогда управление мощностью мотора задается командой
- показания датчика оборотов на моторе А. Тогда управление мощностью мотора задается командой
Motor[MotorA]=k*(45-e1);
Здесь  - усиливающий коэффициент, например 5.
- усиливающий коэффициент, например 5.
При отклонении в положительную сторону на мотор будет подаваться отрицательная мощность и наоборот. Это управление можно применять к мотору в цикле с небольшой задержкой в 1-10 мс, чтобы разгрузить процессор.
Далее, чтобы изменить положение звена, достаточно, имея вместо числа 45 переменную, изменить ее значение из параллельной задачи.
5.1.3. Синхронизация моторов
Довольно часто мы наблюдаем, как тележка, которой сказано двигаться прямо, медленно съезжает с заданного курса. Причин может быть множество: и трение на осях или шестернях, и цепляющаяся за корпус шина, и капризы моторов.
Однако можно построить регулятор, который обеспечит абсолютно синхронное движение моторов. В принципе практически во всех средах есть соответствующие управляющие команды, но они не всегда работают верно. К тому же интересно кое-что сделать самостоятельно.
Итак, задача - двигаться прямолинейно. Пусть  и
и  - показания датчиков оборотов моторов В и С. Их надо будет обнулить перед началом движения. Регулятор определим следующим образом:
- показания датчиков оборотов моторов В и С. Их надо будет обнулить перед началом движения. Регулятор определим следующим образом:
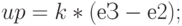
А воздействие на моторы уже знакомо из предыдущих примеров:
Если мотор В обгоняет мотор С, то регулятор станет отрицательным и мотор В начнет притормаживать, а С ускоряться. И наоборот. При этом можно указать и максимальную мощность, поскольку, как правило, отклонения в этом случае довольно малы и достаточно ограничиться понижением мощности обгоняющего мотора.
5.1.4. Взять азимут
Если читателю удалось обзавестись компасом от компании Hitechnic, стоит попробовать и его использовать вместе с П- регулятором.
Задачка проста. Взять азимут и ехать в заданном направлении, никуда не сворачивая. Пусть alpha - азимут, т.е. угол, полученный с компаса на момент старта, a s1 - показания датчика компаса в каждый момент времени.
alpha=s1;
while (true)
{
preg=k*(A-s1);
Motor[MotorB]=50+preg;
Motor[MotorC]=50-preg;
}
Напомним, что для надежности работы компас должен быть отодвинут от моторов и контроллера не менее, чем на 15 см. Кроме того, желательно, чтобы поблизости не было сильных магнитных полей.
5.1.5. Движение по линии
Поначалу это может показаться странным, но движение по границе черного и белого тоже можно построить на П-регуляторе. Хотя внешне задача представляется решаемой только с помощью релейного регулятора, поскольку в системе присутствует всего два видимых человеческому глазу состояния: черное и белое. Но робот все видит иначе, для него отсутствует резкая граница между этими цветами.
Можно сказать, он близорук и видит градиентный переход оттенков серого. Вот это нам и поможет построить П-регулятор.
Так же как и в релейном регуляторе, необходимо определить среднее значение между черным и белым, обозначим его grey. Это будет то состояние датчика освещенности s1, к которому должна стремиться система.
while(true)
{
up=k*(s1-grey);
motor[MotorB]=50+up;
motor[MotorC]=50-up;
wait1msec(1);
}
Коэффициент  может быть достаточно мал (от 1 до 3) для маневренного устройства.
может быть достаточно мал (от 1 до 3) для маневренного устройства.
Такой регулятор эффективно работает только для малых углов отклонения, поэтому устройство надо ставить в направлении движения так, чтобы датчик оказался по левую сторону от черной линии. Если датчик заедет на черную линию, регулятор станет отрицательным и левый мотор будет ехать медленнее правого, что выровняет робота. Нетрудно заметить, что движение по линии на П-регуляторе отличается плавностью и на некоторых участках робот движется практически прямолинейно, или точно повторяя изгибы линии.



