Математические принципы реализации автоматического управления

5.1.6. Движение по линии с двумя датчиками

Этот регулятор интересен тем, что на него практически не влияют колебания освещенности в помещении, которые обычно доставляют немало проблем начинающим робототехникам.

Как же использовать то, что мы имеем? Давайте размышлять. Релейный регулятор на двух датчиках работает известным образом: при двух белых едет прямо, при одном черном поворачивает в сторону черного, при двух черных едет прямо.

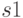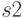Из первого и третьего утверждений можно заметить, что при равных показаниях датчиков робот едет прямо. Учитывая наши знания о зрении робота, можно утверждать, что при любых равных значениях показаний датчиков (в том числе и на сером) робот должен ехать прямо. Предположим, что наши датчики и откалиброваны абсолютно одинаково, и построим регулятор для идеальной системы, который будет равен нулю при равных показаниях.

up=k1*(s1-s2);
    Motor[MotorB]=50+up;
    Motor[MotorC]=50-up;
    

Если на левом датчике 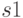потемнеет, управление и станет отрицательным, мотор В станет медленнее, чем С, и робот начнет подруливать влево. И наоборот. Все сходится.

Теперь спустимся с небес на землю. Может оказаться, что датчики откалиброваны по-разному. Для этого следует приспособиться под их показания, т.е. произвести автокалиброку перед запуском. И сравниваться в регуляторе будут не абсолютные показания, а их отклонения.

left=s1; 
    right=s2; 
    while (true)
    {
      up=k1*((s1-left)-(s2-right));
      Motor[MotorB]=50+up;
      Motor[MotorC]=50-up; 
      wait1msec(1);
    }
    

Коэффициент 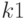может изменяться в достаточно широком диапазоне (от 1 до 20 и более) в зависимости от кривизны линии, манёвренности робота и разницы между черным и белым на поле.

Важное условие. Автокалибровка должна производиться на одноцветной поверхности и желательно при той освещенности, которая будет занимать наибольшую часть пути. Например, если устройство едет вдоль черной линии на белом поле, то калиброваться надо на белом.

И еще замечание. Встречаются датчики, показания которых расходятся на 10-20%. Желательно их не ставить в паре на регулятор с большим коэффициентом, поскольку при резком изменении общей освещенности даже на белом поле отклонения могут несколько разойтись, что может привести к неожиданным последствиям.

5.1.7. Движение вдоль стенки

Решим такую задачу. Робот должен двигаться вдоль стенки на заданном расстоянии L. Предположим, что левое колесо робота управляется мотором В, правое - мотором С, а датчик расстояния, подключенный к порту 1, закреплен несколько впереди корпуса тележки (это важно!) и направлен на стенку справа по ходу движения.

Рис. 5.6.

Расстояние до стенки в настоящий момент времени, которое показывает датчик, обозначим .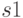

Моторы двигаются со средней скоростью 50, но при отклонении от заданного курса на них осуществляется управляющее воздействие up. Снова обозначим это следующим образом.

    Motor[MotorB]=50+up;
    Motor[MotorC]=50-up;
    

Осталось определить, чему будет равно управляющее воздействие. Это нетрудно:

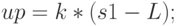
Таким образом, при робот не меняет курса и едет прямо. В случае отклонения его курс корректируется. Здесь - это некоторый усиливающий коэффициент, определяющий воздействие регулятора на систему. Для робота NXT средних размеров коэффициент k может колебаться от 1 до 10 в зависимости от многих факторов. Предлагаем подобрать его самостоятельно.

В данном случае регулятор будет эффективно работать только при малых углах отклонения. Кроме того, движение практически всегда будет происходить по волнообразной траектории. Сделать регулирование более точным позволит введение новых принципов, учитывающих отклонение робота от курса.

5.1.8. Пропорционально-дифференциальный регулятор

Рис. 5.7.

В некоторых ситуациях П-регулятор может вывести систему из устойчивого состояния. Например, если робот направлен от стенки, но находится к ней ближе заданного расстояния, на моторы поступит команда еще сильнее повернуть от стенки, в результате чего с ней может быть утерян контакт (напоминаем, что датчик расстояния получает отраженный сигнал практически только от перпендикулярной поверхности).

Рис. 5.8.

Для защиты от подобных ситуаций добавим в регулятор дифференциальную составляющую, которая будет следить за направлением движения робота. Иными словами, вектор скорости будет влиять на управляющее воздействие. Известно, что скорость находится как , где - это изменение расстояния за промежуток времени . Определим дифференциальный регулятор через скорость отклонения робота от заданного положения:

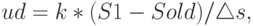
где 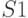- текущее расстояние до стенки, - расстояние на предыдущем шаге.

Поскольку замеры производятся через равные промежутки времени, то можно принять за константу.

Таким образом, ПД-регулятор описывается формулой из двух слагаемых

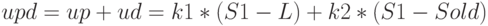
Можно показать, что для устойчивого достижения цели коэффициент 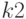при дифференциальной составляющей должен превышать 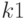(см. ниже статью "Элементы теории автоматического управления в школе").

Алгоритм движения вдоль стенки на ПД-регуляторе в целом будет выглядеть так:

Sold=L=S1; 
    while(true)
    {
    upd= k1*(S1-L) + k2*(S1-Sold); 

    Motor[MotorB]=50+upd;
    Motor[MotorC]=50-upd;

    Sold=S1; 
    wait1msec(1);
    }
    

Для объезда предметов потребуется ввести контроль показаний датчика расстояния: при резком изменении робот должен делать вывод о возможном повороте, который надо будет производить с другими коэффициентами.