|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
Определение базисов Гребнера
Следующей рассматриваемой задачей будет задача выбора канонического
представления для элементов кольца регулярных на некотором
алгебраическом многообразии функций. Это кольцо представляет собой
факторкольцо кольца многочленов ![R = K[x_1, \dots, x_n]](/sites/default/files/tex_cache/e4e484327ebc725ead6fd9b2462dfa84.png) , где
, где  -
поле, по некоторому
идеалу
-
поле, по некоторому
идеалу  . Предполагаем, что идеал
. Предполагаем, что идеал  задан конечной
системой
образующих:
задан конечной
системой
образующих:  . Теорема Гильберта о базисе
утверждает,
что таким образом может быть задан любой идеал кольца многочленов
. Теорема Гильберта о базисе
утверждает,
что таким образом может быть задан любой идеал кольца многочленов 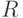 .
Любой элемент факторкольца
.
Любой элемент факторкольца  - это смежный класс
элементов кольца
- это смежный класс
элементов кольца 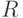 относительно идеала
относительно идеала  . При фиксированном каноническом
представлении
элементов кольца
. При фиксированном каноническом
представлении
элементов кольца 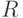 , задача о представлении элементов факторкольца
, задача о представлении элементов факторкольца  сводится к задаче выбора канонического представителя в смежном классе.
Будем пытаться решить ее в следующей формулировке: в кольце многочленов
сводится к задаче выбора канонического представителя в смежном классе.
Будем пытаться решить ее в следующей формулировке: в кольце многочленов ![R = K[x_1, \dots, x_n]](/sites/default/files/tex_cache/e4e484327ebc725ead6fd9b2462dfa84.png) дано конечное множество элементов
дано конечное множество элементов 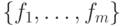 .
Требуется построить алгоритм, который для любого многочлена
.
Требуется построить алгоритм, который для любого многочлена 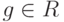 выбирал
бы канонического представителя в соответствующем смежном классе по
идеалу
выбирал
бы канонического представителя в соответствующем смежном классе по
идеалу  .
.
Кольцо многочленов 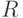 можно рассматривать как бесконечномерное
векторное пространство над полем
можно рассматривать как бесконечномерное
векторное пространство над полем  , базис которого образует
счетное множество мономов
, базис которого образует
счетное множество мономов 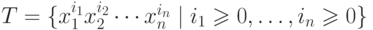 . Идеал
. Идеал  , а, следовательно, и факторкольцо
, а, следовательно, и факторкольцо  , также
являются векторными
, также
являются векторными  -пространствами. Наша задача состоит в построении отображения
-пространствами. Наша задача состоит в построении отображения 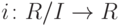 , правого обратного к каноническому гомоморфизму
, правого обратного к каноническому гомоморфизму  , т. е.
, т. е.  для любого
для любого  , Таким образом, мы получаем
разложение
, Таким образом, мы получаем
разложение 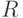 в
прямую сумму векторных пространств
в
прямую сумму векторных пространств  и
и  .
Задачу выбора
канонического представления решает тогда отображение
.
Задачу выбора
канонического представления решает тогда отображение  ,
получающееся проектированием прямой суммы векторных пространств на одно
из слагаемых. Достаточно выбрать новый базис кольца
,
получающееся проектированием прямой суммы векторных пространств на одно
из слагаемых. Достаточно выбрать новый базис кольца 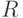 ,
рассматриваемого
как векторное
,
рассматриваемого
как векторное  -пространство, пересечение которого с идеалом
-пространство, пересечение которого с идеалом  представляет базис векторного пространства
представляет базис векторного пространства  .
.
8.1. ПРИМЕР.
Пусть идеал  является мономиальным, т. е. порожден мономами
является мономиальным, т. е. порожден мономами  . Тогда
. Тогда  является базисом
векторного пространства
является базисом
векторного пространства  , а
, а  - базисом факторкольца
- базисом факторкольца  ,
рассматриваемого как векторное
пространство. Каноническое представление получается, если в разложении
любого многочлена по базису
,
рассматриваемого как векторное
пространство. Каноническое представление получается, если в разложении
любого многочлена по базису  отбрасывать элементы, принадлежащие
отбрасывать элементы, принадлежащие  .
.
Хотя только что рассмотренный пример носит частный характер, он
указывает на общий подход к решению поставленной задачи: выбрать такой
базис векторного пространства 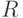 , пересечение которого с идеалом
, пересечение которого с идеалом  представляет собой базис векторного пространства
представляет собой базис векторного пространства  .
.
8.2. ПРЕДЛОЖЕНИЕ. Пусть  - векторное пространство (возможно,
бесконечномерное) и
- векторное пространство (возможно,
бесконечномерное) и  - его подпространство.
Предположим, что базис
- его подпространство.
Предположим, что базис 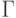 векторного пространства
векторного пространства  выбран таким образом, что
выбран таким образом, что  представляет
собой базис пространства
представляет
собой базис пространства 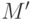 . Тогда каноническое представление
факторпространства
. Тогда каноническое представление
факторпространства  в
в  получается, если базис
пространства
получается, если базис
пространства  отождествить с
отождествить с  .
.
ДОКАЗАТЕЛЬСТВО
получается немедленно из разложения векторного
пространства  в прямую сумму векторных пространств с базисами
в прямую сумму векторных пространств с базисами  и
и  ,
которые изоморфны пространствам
,
которые изоморфны пространствам 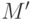 и
и  соответственно.
соответственно.
Пусть идеал  порожден многочленами
порожден многочленами  . Обозначим
. Обозначим  . Тогда счетное множество многочленов
. Тогда счетное множество многочленов  порождает векторное пространство
порождает векторное пространство  , однако эти многочлены не
являются
линейно независимыми. Наша ближайшая задача состоит в построении
достаточно простого алгоритма выбора в множестве
, однако эти многочлены не
являются
линейно независимыми. Наша ближайшая задача состоит в построении
достаточно простого алгоритма выбора в множестве  линейно
независимого подмножества. Для этого построим отображение
линейно
независимого подмножества. Для этого построим отображение  ,
такое, что прообразы различных элементов из
,
такое, что прообразы различных элементов из  линейно независимы,
и
выберем в прообразе каждого элемента единственного представителя (если
этот прообраз не пуст). Получим систему
линейно независимы,
и
выберем в прообразе каждого элемента единственного представителя (если
этот прообраз не пуст). Получим систему 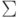 линейно
независимых векторов в
идеале
линейно
независимых векторов в
идеале  , которая, однако, может не порождать идеал
, которая, однако, может не порождать идеал  как векторное
пространство.
как векторное
пространство.
Следующими задачами являются: проверка, порождает ли получившееся линейно
независимое множество векторное пространство  , и если ответ
отрицательный, то пополнение его до базиса.
, и если ответ
отрицательный, то пополнение его до базиса.
Предположим, что множество  упорядочено таким образом, что:
упорядочено таким образом, что:
-
 для любого монома
для любого монома  ;
; - если
 , то
, то 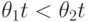 для любого монома
для любого монома 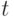 .
.
Как уже сказано в параграфе 3.1, наиболее часто используются следующие три отношения порядка:
- лексикографическое упорядочение мономов, получающееся из фиксированного порядка на множестве переменных;
- упорядочение мономов по степеням, а мономы одной и той же степени упорядочиваются лексикографически;
- упорядочение мономов по степеням, а мономы одной и той же степени упорядочиваются в обратном лексикографическом порядке.
Отображение  ставит в соответствие любому многочлену
ставит в соответствие любому многочлену  его старший моном
(присутствующий в
его старший моном
(присутствующий в  с ненулевым коэффициентом).
с ненулевым коэффициентом).
8.3. УПРАЖНЕНИЕ. Показать, что многочлены с различными старшими мономами линейно независимы.
8.4. УПРАЖНЕНИЕ.
Показать, что свойство системы 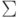 порождать или не
порождать векторное пространство
порождать или не
порождать векторное пространство  не зависит от выбора
представителей в
прообразах элементов из
не зависит от выбора
представителей в
прообразах элементов из  .
.
8.5. УПРАЖНЕНИЕ.
Показать, что система 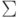 порождает векторное пространство
порождает векторное пространство  тогда и только тогда, когда полугруппа, порожденная в
тогда и только тогда, когда полугруппа, порожденная в  старшими
мономами элементов множества
старшими
мономами элементов множества 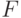 , совпадает с полугруппой старших
мономов
элементов идеала
, совпадает с полугруппой старших
мономов
элементов идеала  .
.
8.6. УПРАЖНЕНИЕ.
Показать, что система 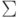 порождает векторное пространство
порождает векторное пространство  тогда и только тогда, когда идеал, порожденный старшими мономами
элементов множества
тогда и только тогда, когда идеал, порожденный старшими мономами
элементов множества 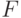 , совпадает с ассоциированным градуированным
идеалом идеала
, совпадает с ассоциированным градуированным
идеалом идеала  (относительно фильтрации с одномерными факторами,
определяемой введенным отношением порядка).
(относительно фильтрации с одномерными факторами,
определяемой введенным отношением порядка).
Рассматриваемая ситуация укладывается в следующую более общую схему:
имеется градуированное некоторым вполне упорядоченным множеством
векторное пространство  с одномерными однородными
компонентами.
Фиксирован базис
с одномерными однородными
компонентами.
Фиксирован базис 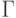 этих компонентов. На пространстве
этих компонентов. На пространстве  рассматривается
фильтрация, совместная с градуировкой. Выбирается множество
рассматривается
фильтрация, совместная с градуировкой. Выбирается множество  элементов
фильтрованного пространства
элементов
фильтрованного пространства  , такое, что при переходе к
градуированному
пространству
, такое, что при переходе к
градуированному
пространству  различные элементы множества
различные элементы множества  переходят в различные
элементы множества
переходят в различные
элементы множества 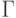 . Тогда множество
. Тогда множество  является базисом
пространства
является базисом
пространства  и определяет разложение пространства
и определяет разложение пространства  в прямую сумму
подпространств
в прямую сумму
подпространств 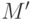 и
и  , где
, где 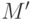 -
пространство с базисом
-
пространство с базисом  , а
пространство
, а
пространство  изоморфно факторпространству
изоморфно факторпространству  и, следовательно,
определяет каноническое представление пространства
и, следовательно,
определяет каноническое представление пространства  в
в  .
.
В случае кольца многочленов градуировка осуществляется полугруппой  ,
где
,
где  - множество неотрицательных целых чисел. В
дальнейшем мы будем
рассматривать также градуировку множеством
- множество неотрицательных целых чисел. В
дальнейшем мы будем
рассматривать также градуировку множеством 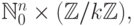 где к свободной
коммутативной полугруппе добавляется конечная. Такое множество
соответствует, например, свободному конечнопорожденному модулю над
кольцом многочленов (не обязательно коммутативных). Конечная компонента
соответствует образующим свободного модуля. Примеры упорядочений
рассматривались в пункте 3.1.
где к свободной
коммутативной полугруппе добавляется конечная. Такое множество
соответствует, например, свободному конечнопорожденному модулю над
кольцом многочленов (не обязательно коммутативных). Конечная компонента
соответствует образующим свободного модуля. Примеры упорядочений
рассматривались в пункте 3.1.
Вернемся к рассмотрению полиномиальных идеалов. Как уже отмечалось, в
качестве базиса 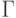 выбирается множество мономов
выбирается множество мономов  . Утверждение о том, что
. Утверждение о том, что 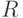 является градуированным векторным пространством с базисом
является градуированным векторным пространством с базисом  ,
означает,
что любой многочлен можно записать в виде
,
означает,
что любой многочлен можно записать в виде  ,
,  , где
, где  для всех
для всех  .
Переход от фильтрации к градуировке означает выделение старшего
одночлена:
.
Переход от фильтрации к градуировке означает выделение старшего
одночлена:  .
.
В частности, такое представление имеет место для всех образующих  идеала
идеала  , причем мы можем выбрать эти образующие так, чтобы
старшие
коэффициенты у них были равны 1, так как мы предполагаем, что
, причем мы можем выбрать эти образующие так, чтобы
старшие
коэффициенты у них были равны 1, так как мы предполагаем, что  - поле:
- поле:
 |
( 8.1) |
В качестве  можно выбрать любое подмножество
можно выбрать любое подмножество  , где
, где  - произвольная система образующих идеала
- произвольная система образующих идеала  ,
руководствуясь двумя
требованиями: во-первых, различные элементы множества
,
руководствуясь двумя
требованиями: во-первых, различные элементы множества  должны иметь
разные старшие мономы; во-вторых, система
должны иметь
разные старшие мономы; во-вторых, система 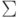 должна быть
максимальна в том
смысле, что для любого элемента
должна быть
максимальна в том
смысле, что для любого элемента  существует
элемент
существует
элемент  с таким же
старшим мономом. Например, можно включить в
с таким же
старшим мономом. Например, можно включить в 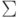 множество
множество  , далее
добавить к нему те элементы множества
, далее
добавить к нему те элементы множества  , старшие мономы
которых
отличаются от старших мономов всех элементов, уже включенных в множество
, старшие мономы
которых
отличаются от старших мономов всех элементов, уже включенных в множество 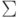 и т.д.
и т.д.
8.7. ОПРЕДЕЛЕНИЕ.
Систему образующих 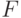 идеала
идеала  назовем базисом Гребнера
этого идеала, если подмножество
назовем базисом Гребнера
этого идеала, если подмножество 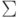 , введенное выше, образует
базис
векторного пространства
, введенное выше, образует
базис
векторного пространства  .
.
Из сформулированных выше упражнений следует корректность определения
базиса Гребнера, т.е. независимость его от конкретного выбора множества 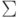 .
.
8.8. ПРИМЕР.
Пусть  - главный идеал, порожденный многочленом
- главный идеал, порожденный многочленом  . Тогда
. Тогда  является базисом Гребнера идеала
является базисом Гребнера идеала  .
.
8.9. ПРИМЕР.
Многочлены  и
и 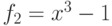 не составляют
базис
Гребнера порождаемого ими идеала в кольце
не составляют
базис
Гребнера порождаемого ими идеала в кольце ![\mathbb Q[x]](/sites/default/files/tex_cache/f3d1f8b27dd29107881f26927fbcc385.png) . Доказать.
. Доказать.
В следующих примерах рассматривается кольцо многочленов ![K[x_1,
\dots,
x_n]](/sites/default/files/tex_cache/57c6cdf6da415af666cbd3214709ca45.png) , которое содержит идеал
, которое содержит идеал  , заданный множеством
образующих
, заданный множеством
образующих  . Предполагается, что одночлены в записи элементов
. Предполагается, что одночлены в записи элементов  упорядочены в
соответствии с одним из введенных выше отношений порядка и нормированы
таким образом, что их старшие коэффициенты равны 1.
упорядочены в
соответствии с одним из введенных выше отношений порядка и нормированы
таким образом, что их старшие коэффициенты равны 1.
8.10. ПРИМЕР.
Если ![I = K[x_1, \dots, x_n]](/sites/default/files/tex_cache/a3af1bb6b00ff4640f80067f9da77b4f.png) , то
, то 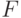 является базисом
Гребнера
идеала
является базисом
Гребнера
идеала  тогда и только тогда, когда
тогда и только тогда, когда  .
.
8.11. ПРИМЕР.
Если поле  алгебраически замкнуто и
алгебраически замкнуто и  -
максимальный идеал, то
-
максимальный идеал, то  является базисом Гребнера
идеала
является базисом Гребнера
идеала  тогда и
только тогда, когда для любой переменной
тогда и
только тогда, когда для любой переменной  найдется элемент
найдется элемент  со
старшим мономом
со
старшим мономом  .
.
8.12. ПРИМЕР.
Если поле  не является алгебраически замкнутым, то утверждение
предыдущего примера неверно.
не является алгебраически замкнутым, то утверждение
предыдущего примера неверно.
Следует заметить, что введенное выше определение базиса Гребнера не является конструктивным: не указано алгоритма для проверки, что некоторая система многочленов представляет базис Гребнера порождаемого ими идеала, и тем более не дан алгоритм, позволяющий для идеала, заданного некоторой системой образующих, построить его базис Гребнера.
В следующем параграфе определение базиса Гребнера будет дано в более общей ситуации, а также будут приведены алгоритмы проверки, является ли данная система образующих идеала его базисом Гребнера, и, в случае отрицательного ответа, - алгоритм, позволяющий пополнить эту систему до базиса Гребнера.
