Моделирование с Maxima

6.3 Моделирование динамических систем

Многие модели, основанные на нелинейных дифференциальных уравнениях, демонстрируют совершенно удивительные свойства, причем решение большинства из них можно получить лишь численно.

Модели, основанные на задачах Коши для ОДУ, часто называют динамическими системами, подчёркивая, что, как правило, они содержат производные по времени и описывают динамику некоторых параметров. Проблемы, связанные с динамическими системами, на самом деле весьма разнообразны и зачастую не сводятся к простому интегрированию ОДУ.

6.3.1 Моделирование системы химических реакций

Рассмотрим другой пример. Исследуем систему из трех дифференциальных уравнений, описывающих модель химической кинетики:

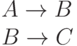
Система соответствующих дифференциальных уравнений

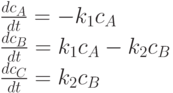
Начальные условия:

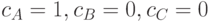
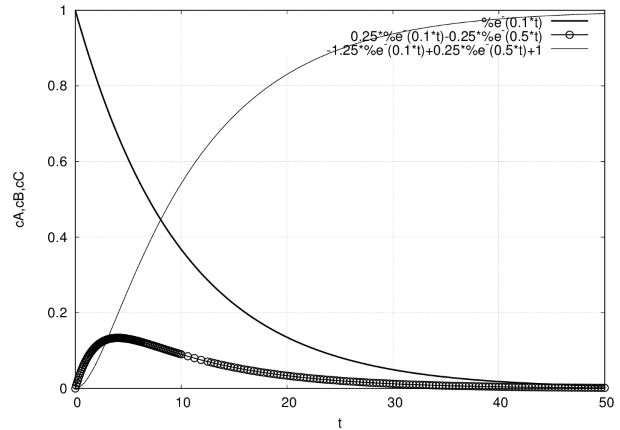
Результаты решения приведены на рис.6.6.

увеличить изображение
Рис. 6.6. Кинетика химических реакций

(%i1)	eq1:'diff(ca(t),t)=-k1*ca(t);
	eq2:'diff(cb(t),t)=k1*ca(t)-k2*cb(t);
	eq3:'diff(cc(t),t)=k2*cb(t);

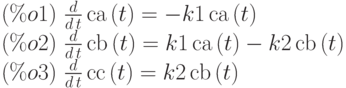
(%i4)	atvalue(ca(t),t=0,1);

(%i5)	atvalue(cb(t),t=0,0);
	atvalue(cc(t),t=0,0);

(%i7)	sol:desolve([eq1,eq2,eq3],[ca(t),cb(t),cc(t)]);

(%i8)	ratsimp(sol);

(%i9)	k1:0.1; k2:0.5; ev((sol));

(%i12)	plot2d([%e^(-0.1*t),0.25*%e^(-0.1*t)-0.25*%e^(-0.5*t),
-1.25*%e^(-0.1*t)+0.25*%e^(-0.5*t)+1],[t,0,50],
	[gnuplot_preamble,"set grid"],
	[gnuplot_term,"png size 500,500"],
	[gnuplot_out_file,"chem.png"]);

Несколько более сложная задача — моделирование кинетики параллельно-последовательных реакций, протекающих по схеме:

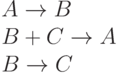
В зависимости от констант скорости химических реакций данная система может быть довольно жёсткой.

Пример командного файла для решения жёсткой системы ОДУ в Maxima (данная система нелинейна, поэтому используем метод Рунге-Кутта, однако расчёты затрудняются жёсткостью системы):

load("dynamics");
load("draw");
k1:0.1; k2:100; k3:10;
eq1:-k1*ca+k3*cb*cc;
eq2:k1*ca-k3*cb*cc-k2*cb;
eq3:k2*cb;
t_range:[t,0,100,0.01];
sol: rk([eq1,eq2,eq3],[ca,cb,cc],[1,0,0],t_range)$
len:length(sol);
t:makelist(sol[k][1],k,1,len)$
ca:makelist(sol[k][2],k,1,len)$
cb:makelist(sol[k][3],k,1,len)$
cc:makelist(sol[k][4],k,1,len)$
draw2d(title="Chemical system",xlabel="ca",ylabel="cb",
	grid=true,points_joined =true,points(t,ca),
	points(t,cb),points(t,cc),terminal=eps);

Данная система достаточно трудно решается при помощи функции 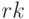. Увеличение констант до 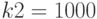и 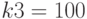делает задачу практически неразрешимой средствами пакета dynamics.

Простейшим классическим примером существования автоколебаний в системе химических реакций является тримолекулярная модель "Брюсселятор", предложенная в Брюсселе Пригожиным и Лефевром (1965). Основной целью при изучении этой модели было установление качественных типов поведения, совместимых с фундаментальными законами химической и биологической кинетики. В этом смысле брюсселятор играет роль базовой модели, такую же как гармонический осциллятор в физике, или модели Вольтерра в динамике популяций.

увеличить изображение
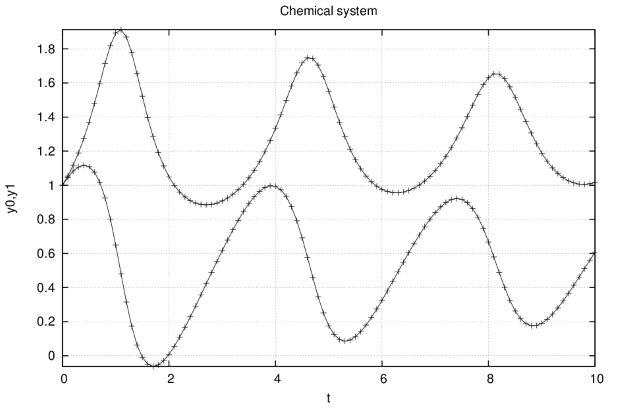
Рис. 6.7. Изменение концентраций при моделировании автоколебательной химической реакции (брюсселятора)

В рамках данной книги брюсселятор рассматривается как пример автоколебательной системы.

Описание модели брюсселятора в Maxima приведено в следующем командном файле:

load("dynamics");
load("draw");
B:0.5;
eq1:-(B+1)*y0+y0^2*y1+1;
eq2:B*y0-y0^2+1;
t_range:[t,0,10,0.1];
sol: rk([eq1,eq2],[y0,y1],[1,1],t_range)$
len:length(sol);
t:makelist(sol[k][1],k,1,len)$
y0:makelist(sol[k][2],k,1,len)$
y1:makelist(sol[k][3],k,1,len)$
draw2d(title="Brusselator",xlabel="t",ylabel="y0,y1",
grid=true,points_joined = true,
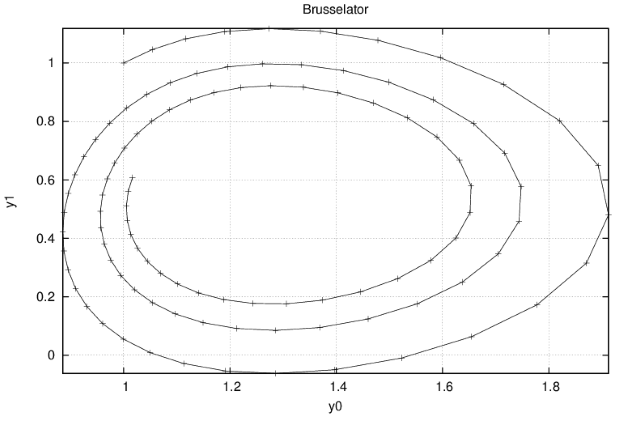
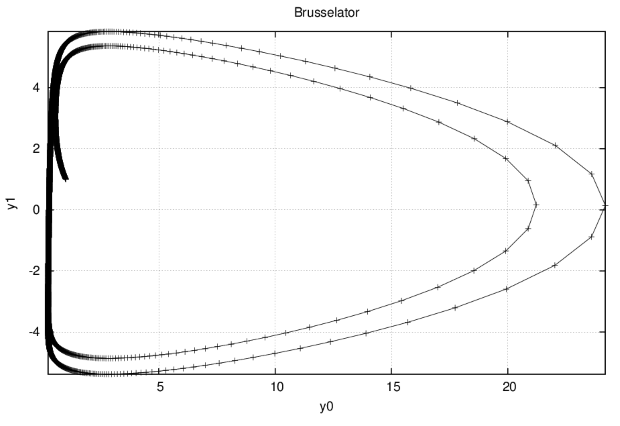
points(t,y0),points(t,y1),terminal=eps);

Графическая иллюстрация (автоколебательный режим в системе) — на рис.67., а фазовые портреты — на рис.6.8 и рис.6.9.

увеличить изображение
Рис. 6.8. Фазовый портрет для брюсселятора (В=0.5)

увеличить изображение
Рис. 6.9. Фазовый портрет для брюсселятора (В=2.5)

При проведении расчётов следует обратить внимание на жёсткость системы ОДУ, описывающей брюсселятор, в частности, при 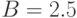для построения приведённой иллюстрации необходимо было уменьшить шаг по времени до 0.002. При очередном запуске командного файла, содержащего команды загрузки пакетов, рекомендуется перезапустить Maxima.