|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Принципы анализа алгоритмов
О-нотация
Математическая запись, позволяющая отбрасывать детали при анализе алгоритмов, называется О-нотацией. Она определена следующим образом.
Определение 2.1. Говорят, что функция 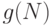 имеет порядок
имеет порядок 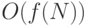 , если существуют такие постоянные
, если существуют такие постоянные  и
и 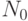 , что
, что 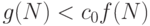 для всех
для всех  .
.
О-нотация используется по трем различным причинам:
- Чтобы ограничить ошибку, возникающую при отбрасывании малых слагаемых в математических формулах.
- Чтобы ограничить ошибку, возникающую при игнорировании частей программы, которые вносят небольшой вклад в анализируемую сумму.
- Чтобы классифицировать алгоритмы по верхним границам их общего времени выполнения.
Третье назначение О-нотации рассматривается в разделе 2.7, а здесь мы обсудим два других.
Постоянные  и
и 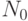 , не выраженные явно в О-нотации, часто скрывают практически важные подробности реализации. Очевидно, что выражение "алгоритм имеет время выполнения
, не выраженные явно в О-нотации, часто скрывают практически важные подробности реализации. Очевидно, что выражение "алгоритм имеет время выполнения 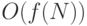 " ничего не говорит о времени выполнения при
" ничего не говорит о времени выполнения при  , меньшем
, меньшем 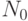 , а
, а  может иметь большое значение, необходимое для работы в наихудшем случае. Понятно, что лучше иметь алгоритм, время выполнения которого составляет
может иметь большое значение, необходимое для работы в наихудшем случае. Понятно, что лучше иметь алгоритм, время выполнения которого составляет  наносекунд, а не
наносекунд, а не  столетий, но мы не можем сделать такой выбор на основе О-нотации.
столетий, но мы не можем сделать такой выбор на основе О-нотации.
Часто результаты математического анализа являются не точными, а приближенными именно в техническом смысле: результат представляет собой сумму убывающих слагаемых. Так же как мы интересуемся в основном внутренним циклом программы, нас интересует больше всего главные члены (наибольшие по величине слагаемые) математического выражения. О-нотация позволяет работать с приближенными математическими выражениями, рассматривая главные члены и опуская меньшие слагаемые, а также записывать краткие выражения, дающие неплохие приближения для анализируемых величин.
Некоторые из основных действий, которые используются при работе с выражениями, содержащими О-нотацию, являются предметом упражнений 2.20 - 2.25. Многие из этих действий интуитивно понятны, а склонные к математике читатели могут с интересом выполнить упражнение 2.21, где требуется доказать верность базовых операций, исходя из определения. По сути, из этих упражнений следует, что в алгебраических выражениях с О-нотацией можно раскрывать скобки так, как будто ее там нет, а затем отбрасывать все слагаемые, кроме наибольшего. Например, если требуется раскрыть скобки в выражении
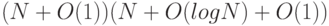 , то мы получим шесть слагаемых
, то мы получим шесть слагаемых
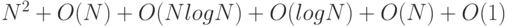 .
.
Однако можно отбросить все О-слагаемые, кроме наибольшего из них, и тогда останется приближенное выражение
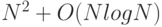 .
.
То есть при больших  хорошей аппроксимацией этого выражения является N^2. Эти действия интуитивно ясны, но О-нотация позволяет выразить их с математической точностью. Формула с одним О-слагаемым называется асимптотическим выражением (asymptotic expression).
хорошей аппроксимацией этого выражения является N^2. Эти действия интуитивно ясны, но О-нотация позволяет выразить их с математической точностью. Формула с одним О-слагаемым называется асимптотическим выражением (asymptotic expression).
В качестве более конкретного примера предположим, что (после некоторого математического анализа) мы выяснили, что определенный алгоритм имеет внутренний цикл, выполняемый в среднем 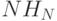 раз, внешний раздел, выполняемый
раз, внешний раздел, выполняемый  раз, и некоторый код инициализации, исполняемый однократно. Далее предположим, что (после тщательного исследования реализации) мы определили, что каждая итерация внутреннего цикла требует
раз, и некоторый код инициализации, исполняемый однократно. Далее предположим, что (после тщательного исследования реализации) мы определили, что каждая итерация внутреннего цикла требует  наносекунд, внешний раздел -
наносекунд, внешний раздел - 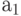 наносекунд, а код инициализации -
наносекунд, а код инициализации -  наносекунд. Тогда среднее время выполнения программы (в наносекундах) равно
наносекунд. Тогда среднее время выполнения программы (в наносекундах) равно
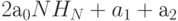 .
.
Поэтому для времени выполнения справедлива следующая формула:
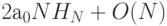 .
.
Эта более простая формула важна, поскольку из нее следует, что для аппроксимации времени выполнения при больших  нет необходимости искать значения величин
нет необходимости искать значения величин 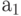 и
и  2
. В общем случае, в точном математическом выражении для времени выполнения может содержаться множество других слагаемых, ряд которых трудно анализировать. О-нотация обеспечивает способ получения приближенного ответа для больших
2
. В общем случае, в точном математическом выражении для времени выполнения может содержаться множество других слагаемых, ряд которых трудно анализировать. О-нотация обеспечивает способ получения приближенного ответа для больших  , не заботясь о подобных слагаемых.
, не заботясь о подобных слагаемых.
Далее, О-нотация позволяет в данном примере выразить время выполнения через более знакомую функцию 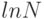 . С помощью
таблица
2.3 полученное выражение можно приближенно записать как
. С помощью
таблица
2.3 полученное выражение можно приближенно записать как 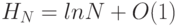 . Таким образом, асимптотическое выражение для общего времени выполнения алгоритма имеет вид
. Таким образом, асимптотическое выражение для общего времени выполнения алгоритма имеет вид 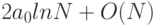 . То есть при больших
. То есть при больших  оно будет близко к легко вычисляемому выражению
оно будет близко к легко вычисляемому выражению  . Постоянный множитель
. Постоянный множитель  зависит от времени выполнения инструкций внутреннего цикла.
зависит от времени выполнения инструкций внутреннего цикла.
Более того, нам не нужно знать значения 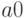 , чтобы предсказать, что при больших
, чтобы предсказать, что при больших  время выполнения для входных данных размером
время выполнения для входных данных размером 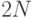 будет вдвое больше, чем для входных данных размером
будет вдвое больше, чем для входных данных размером  , поскольку
, поскольку
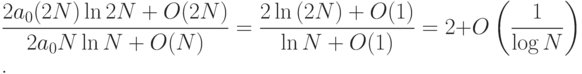
Таким образом, асимптотическая формула позволяет нам делать точные прогнозы, не вдаваясь в подробности реализации или анализа. Отметьте, что такое предсказание не было бы возможным, если бы О-аппроксимация была задана только для главного члена.
Описанный способ рассуждений позволяет ограничиться только главным членом при сравнении или предсказании времени выполнения алгоритмов. Очень часто требуется подсчитать количество выполнения операций с фиксированным временем выполнения и ограничиться только главным членом, подразумевая неявно, что при необходимости можно всегда провести точный анализ наподобие приведенного выше.
Когда функция 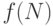 асимптотически велика по сравнению с другой функцией
асимптотически велика по сравнению с другой функцией  (т.е.
(т.е. 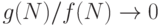 при
при 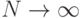 ), иногда в данной книге мы будем использовать термин (конечно, неточный) порядка
), иногда в данной книге мы будем использовать термин (конечно, неточный) порядка 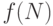 , что означает
, что означает 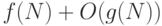 . Потеря математической точности компенсируется большей наглядностью, так как нас больше интересует производительность алгоритмов, а не математические детали. В таких случаях мы можем быть уверены в том, что при больших (а, может, даже и всех) значениях
. Потеря математической точности компенсируется большей наглядностью, так как нас больше интересует производительность алгоритмов, а не математические детали. В таких случаях мы можем быть уверены в том, что при больших (а, может, даже и всех) значениях  исследуемая величина будет близка к
исследуемая величина будет близка к 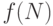 . Например, даже если мы знаем, что некоторая величина равна
. Например, даже если мы знаем, что некоторая величина равна  , ее можно рассматривать как
, ее можно рассматривать как 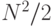 . Такой способ выражения результатов более понятен, чем подробный и точный результат, и, к примеру, при
. Такой способ выражения результатов более понятен, чем подробный и точный результат, и, к примеру, при 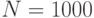 отличается от правильного значения всего лишь на 0,1%. Потеря точности в данном случае намного меньше, чем при распространенном использовании
отличается от правильного значения всего лишь на 0,1%. Потеря точности в данном случае намного меньше, чем при распространенном использовании 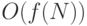 . При описании производительности алгоритмов мы будем по возможности стараться быть и точными, и краткими.
. При описании производительности алгоритмов мы будем по возможности стараться быть и точными, и краткими.
В похожем ключе мы иногда говорим, что время выполнения алгоритма пропорционально 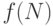 , т.е. можно доказать, что оно равно с
, т.е. можно доказать, что оно равно с 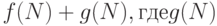 асимптотически мало по сравнению с
асимптотически мало по сравнению с 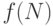 . При таком подходе можно предсказать время выполнения для
. При таком подходе можно предсказать время выполнения для 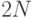 , если оно известно для
, если оно известно для  , как в рассмотренном выше примере. На рис. 2.3
рис.
2.3 приводятся значения множителей для таких прогнозов поведения функций, которые часто возникают при анализе алгоритмов. В сочетании с эмпирическим изучением (см. раздел 2.1) данный подход освобождает от определения постоянных величин, зависящих от реализации. Или же, применяя его в обратном направлении, зачастую мы можем выдвинуть гипотезу о функциональной зависимости времени выполнения программы, изучив, как меняется время выполнения при удвоении
, как в рассмотренном выше примере. На рис. 2.3
рис.
2.3 приводятся значения множителей для таких прогнозов поведения функций, которые часто возникают при анализе алгоритмов. В сочетании с эмпирическим изучением (см. раздел 2.1) данный подход освобождает от определения постоянных величин, зависящих от реализации. Или же, применяя его в обратном направлении, зачастую мы можем выдвинуть гипотезу о функциональной зависимости времени выполнения программы, изучив, как меняется время выполнения при удвоении  .
.
Различия между О-оценками пропорционально (is proportional to) и порядка (about) проиллюстрированы на рис. 2.4 и рис. 2.5. О-нотация используется, прежде всего, для исследования фундаментального асимптотического поведения алгоритма; пропорционально требуется при экстраполяции производительности на основе эмпирического изучения, а порядка - при сравнении производительности или при предсказании абсолютной производительности.
Нетрудно предсказать влияние удвоения размеров задачи на время выполнения, если время выполнения пропорционально одной из простых функций, указанных в таблице. Теоретически это влияние можно вычислить только для больших  , но данный метод на удивление эффективен.
И наоборот, быстрый метод определения функционального роста времени выполнения программы заключается в запуске программы, удвоении объема входных данных для максимально возможного
, но данный метод на удивление эффективен.
И наоборот, быстрый метод определения функционального роста времени выполнения программы заключается в запуске программы, удвоении объема входных данных для максимально возможного  , а затем оценка функциональной зависимости согласно приведенной таблице.
, а затем оценка функциональной зависимости согласно приведенной таблице.
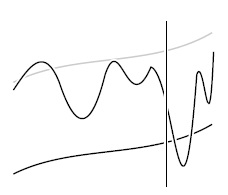
На этой схематической диаграмме осциллирующая кривая представляет собой функцию 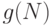 , которую мы пытаемся аппроксимировать; плавная черная кривая представляет собой другую функцию,
, которую мы пытаемся аппроксимировать; плавная черная кривая представляет собой другую функцию, 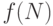 , которая используется для аппроксимации, а плавная серая кривая является функцией
, которая используется для аппроксимации, а плавная серая кривая является функцией  с некоторой неопределенной постоянной
с некоторой неопределенной постоянной  . Вертикальная прямая задает значение
. Вертикальная прямая задает значение 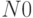 , указывающее, что аппроксимация справедлива для
, указывающее, что аппроксимация справедлива для  . Когда мы говорим, что
. Когда мы говорим, что 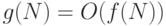 , мы лишь ожидаем, что значение функции
, мы лишь ожидаем, что значение функции 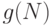 находится ниже некоторой кривой, имеющей форму функции
находится ниже некоторой кривой, имеющей форму функции 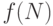 , и правее некоторой вертикальной прямой. Поведение функции
, и правее некоторой вертикальной прямой. Поведение функции 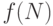 может быть любым (например, она не обязательно должна быть непрерывной).
может быть любым (например, она не обязательно должна быть непрерывной).
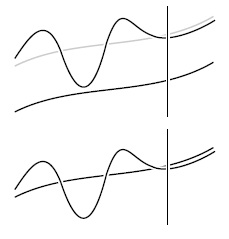
Когда говорят, что функция 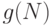 пропорциональна функции
пропорциональна функции 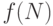 (верхний график), то подразумевают, что она растет как
(верхний график), то подразумевают, что она растет как 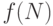 , но, возможно, смещена относительно последней на неизвестный коэффициент. Если задано некоторое значение
, но, возможно, смещена относительно последней на неизвестный коэффициент. Если задано некоторое значение 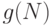 , можно предсказать поведение функции при больших
, можно предсказать поведение функции при больших  . Когда говорят, что
. Когда говорят, что 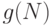 порядка
порядка 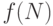 (нижний график), то подразумевают, что функцию
(нижний график), то подразумевают, что функцию  можно использовать для достаточно точной оценки значений функции g.
можно использовать для достаточно точной оценки значений функции g.
Упражнения
 2.20. Докажите, что О(1) - то же самое, что и О(2).
2.20. Докажите, что О(1) - то же самое, что и О(2).
2.21. Докажите, что в выражениях с О-нотацией можно выполнить любое из перечисленных преобразований:
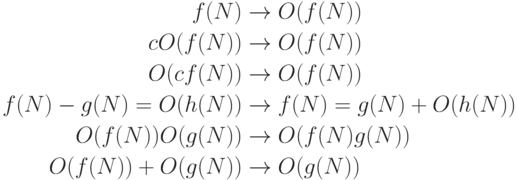
- 2.22. Покажите, что (N + 1)(H_N + O(1)) = N lnN + O(N).
- 2.23. Покажите, что
 .
. - 2.24. Покажите, что
 для любого
для любого  и любого постоянного
и любого постоянного  .
. - 2.25. Докажите, что
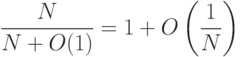
- 2.26. Предположим, что
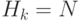 . Найдите приближенную формулу, которая выражает
. Найдите приближенную формулу, которая выражает  как функцию
как функцию  .
. - 2.27. Предположим, что
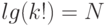 . Найдите приближенную формулу, которая выражает k как функцию
. Найдите приближенную формулу, которая выражает k как функцию  .
. - 2.28. Известно, что время выполнения одного алгоритма равно
 , а другого -
, а другого - 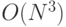 . Что это неявно говорит об относительной производительности алгоритмов?
. Что это неявно говорит об относительной производительности алгоритмов? - 2.29. Известно, что время выполнения одного алгоритма всегда порядка
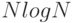 , а другого -
, а другого - 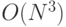 . Что это неявно говорит об относительной производительности алгоритмов?
. Что это неявно говорит об относительной производительности алгоритмов? - 2.30. Известно, что время выполнения одного алгоритма всегда порядка
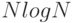 , а другого - всегда
, а другого - всегда  . Что это неявно говорит об относительной производительности алгоритмов?
. Что это неявно говорит об относительной производительности алгоритмов? - 2.31. Известно, что время выполнения одного алгоритма всегда пропорционально
 , а другого - всегда пропорционально
, а другого - всегда пропорционально  . Что это неявно говорит об относительной производительности алгоритмов?
. Что это неявно говорит об относительной производительности алгоритмов? - 2.32. Выведите значения множителей, приведенных на
рис.
2.3: для каждой функции
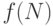 , показанной слева, найдите асимптотическую формулу для
, показанной слева, найдите асимптотическую формулу для 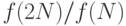 .
.