|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы теории вероятностей и математической статистики
Основные правила для вероятностей:
- правило сложения вероятностей для несовместимых событий S1 и S2:
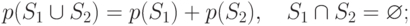
- правило умножения вероятностей для несовместимых событий S1 и S2:
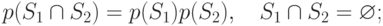
-
условная вероятность события S1 (вероятность появления этого события при условии появления события S2 для каждого события рассматриваемого множества событий) определяется по формуле (Байеса):

- общее правило сложения вероятностей:
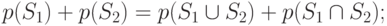
Пример. Лотерейные билеты, двузначные, от 10 до 99. Имеется 1 билет с выигрышем 100 руб., 10 - с выигрышем 50 руб., 20 - с выигрышем в 30 руб. Вероятность того, что вытащенный наугад билет лотереи имеет номер 50 (как и любой другой двузначный номер), равна 1/90. Вероятность того, что у такого билета цифра десятков равна 5, будет 1/9. Вероятность выиграть 100 руб. равна 1/90, а вероятность выиграть хотя бы 30 руб. равна 31/90.
Под случайным событием в теории вероятностей понимается событие, которое в результате испытания может произойти или может не произойти, то есть происходит с некоторой вероятностью, случайно. Случайные события бывают дискретные (принимающие конечные числа, последовательность пронумерованных значений) и непрерывные (принимающие любые значения из некоторого промежутка значений).
Случайная величина - числовая переменная (числовая функция), определенная на выборочном пространстве (или приписываемая некоторому выборочному пространству) таким образом, что каждой точке выборочного пространства соответствует одно и только одно значение этой переменной.
Если множество всех теоретически возможных значений величины x конечно или счетно, то ее называют дискретной случайной величиной .
Пример. Если n - число, выпавшее на игральной кости при ее бросании номер m, то функция n=n(m) - случайная функция. Эта функция имеет выборочное пространство S={1, 2, 3, 4, 5, 6}.
Функция f(x), которая для каждого возможного значения xi, i=1,2,..., n (или i=1,2,..., n,...) дискретной случайной величины x равна вероятности pi=f(xi) появления этого значения, задает распределение вероятностей случайной величины. Таким образом, эта функция задает множество значений, которые может принимать случайная величина, вместе с соответствующими им вероятностями.
Величину M(x), определяемую формулой
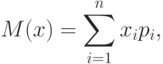
 .
.Величину, определяемую формулой
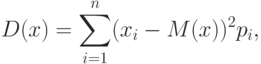
Математическое ожидание характеризует центр распределения (аналог среднего выборки), а дисперсия - степень рассеяния значений случайной величины вокруг центра (аналог рассеяния в выборке). Эти формулы дают возможность получить оценку математического ожидания и дисперсии на основе опытных данных.
Если случайная величина распределена непрерывно и задана некоторой функцией распределения f(x), то M(x) и D(x) определяются по соответствующим формулам (для ограниченного и бесконечного множества изменения случайной величины):
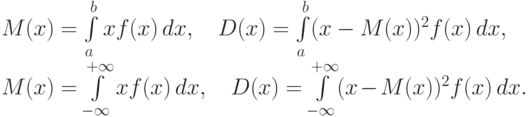
Приведем наиболее часто встречающиеся распределения.
- Распределение Бернулли. Это простейшая форма распределения: случайная величина определена на выборочном пространстве, состоящем из двух только исходов с вероятностями p и q=1-p. Для такой дискретной функции распределения M(x)=p, D(x)=pq=p(1-p).
-
Биноминальное распределение. Пусть случайная величина может принимать целые значения m=0, 1, 2, ..., n. Будем говорить, что эта величина распределена по биноминальному закону, если функция, задающая ее распределение, имеет вид:
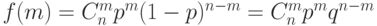 ( 0<p<1, q=1-p ). Для этого распределения M(x)=np, D(x)=npq.
( 0<p<1, q=1-p ). Для этого распределения M(x)=np, D(x)=npq. - Распределение Пуассона. Пусть случайная величина x может принимать любое целое неотрицательное значение m=0, 1, 2, .... Будем говорить, что эта величина распределена по закону Пуассона, если функция, задающая ее распределение, имеет вид: f(m)=am e-a/m!. Здесь a - некоторое положительное число, называемое параметром закона Пуассона. Для этого распределения: M(x)=a, D(x)=a.
-
Нормальное распределение ( распределение Гаусса ). Это наиболее часто встречающееся непрерывное распределение (точнее было бы сказать, что это распределение, к которому "подгоняется" большинство изучаемых). Такому закону или его различным модификациям подчиняются многие наборы случайных величин. Общий вид нормального распределения задается функцией
![f(x)= \frac {1}{\sqrt{2\pi D(X)}} \exp
\bigl[- \frac {(x-M(x))^2}{2D(x)} \bigr].](/sites/default/files/tex_cache/04168811037dac705692e21b40ce34e3.png)

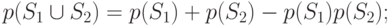
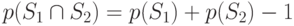 .
.