|
Упражнение 2.1.25 |
Конечные автоматы
Два наиболее распространенных способа конечного задания формального языка - это грамматики и автоматы. Автоматами в данном контексте называют математические модели некоторых вычислительных устройств. В этой лекции рассматриваются конечные автоматы, соответствующие в иерархии Хомского праволинейным грамматикам. Более сильные вычислительные модели будут определены позже, в лекциях "10" , "14" и "15" . Термин "автоматный язык" закреплен за языками, распознаваемыми именно конечными автоматами, а не какими-либо более широкими семействами автоматов (например, автоматами с магазинной памятью или линейно ограниченными автоматами).
В разделе 2.1 определяются понятия конечного автомата (для ясности такой автомат можно называть недетерминированным конечным автоматом) и распознаваемого конечным автоматом языка. В следующем разделе дается другое, но эквивалентное первому определение языка, распознаваемого конечным автоматом. Оно не является необходимым для дальнейшего изложения, но именно это определение поддается обобщению на случаи автоматов других типов.
В разделе 2.3 доказывается, что тот же класс автоматных языков можно получить, используя лишь конечные автоматы специального вида (они читают на каждом такте ровно один символ и имеют ровно одно начальное состояние). Во многих учебниках конечными автоматами называют именно такие автоматы.
Целую серию классических результатов теории формальных языков составляют теоремы о точном соответствии некоторых классов грамматик некоторым классам автоматов. Первая теорема из этой серии, утверждающая, что праволинейные грамматики порождают в точности автоматные языки, доказывается в разделе 2.4.
Другая серия результатов связана с возможностью сузить некоторый класс грамматик, не изменив при этом класс порождаемых ими языков. Обычно в таком случае грамматики из меньшего класса называются грамматиками в нормальной форме. В разделе 2.5* формулируется результат такого типа для праволинейных грамматик. Сама эта теорема не представляет большого интереса, но аналогичные результаты, доказываемые позже для контекстно-свободных грамматик, используются во многих доказательствах и алгоритмах.
Не все конечные автоматы подходят для конструирования распознающих устройств, пригодных для практических приложений, так как в общем случае конечный автомат не дает точного указания, как поступать на очередном шаге, а разрешает продолжать вычислительный процесс несколькими способами. Этого недостатка нет у детерминированных конечных автоматов (частного случая недетерминированных конечных автоматов), определенных в разделе 2.6. В разделе 2.7 доказывается, что каждый автоматный язык задается некоторым детерминированным конечным автоматом.
2.1. Недетерминированные конечные автоматы
Определение 2.1.1. Конечный автомат
(finite automaton, finite-state machine) -
это пятерка 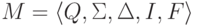 ,
где
,
где 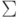 -
конечный входной алфавит
(или просто алфавит ) данного конечного автомата,
-
конечный входной алфавит
(или просто алфавит ) данного конечного автомата, 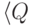 и
и  - конечные множества,
- конечные множества,
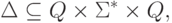
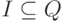 ,
, 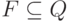 .
Элементы Q
называются состояниями
(state),
элементы I - начальными
(initial) состояниями,
элементы F - заключительными
или допускающими
(final, accepting) состояниями.
Если
.
Элементы Q
называются состояниями
(state),
элементы I - начальными
(initial) состояниями,
элементы F - заключительными
или допускающими
(final, accepting) состояниями.
Если 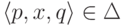 ,
то
,
то  называется переходом
(transition) из p в q,
а слово x - меткой
(label) этого перехода.
называется переходом
(transition) из p в q,
а слово x - меткой
(label) этого перехода.Пример 2.1.2.
Пусть Q = {1,2}, 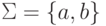 , I = {1}, F = {2},
, I = {1}, F = {2},

 -
конечный автомат.
-
конечный автомат.Замечание 2.1.3.
Конечные автоматы можно изображать в виде диаграмм состояний
(state diagram) (иногда их называют диаграммами переходов
(transition diagram)).
На диаграмме каждое состояние обозначается кружком,
а переход - стрелкой.
Стрелка из p в q,
помеченная словом x,
показывает, что  является переходом данного конечного автомата.
Каждое начальное состояние распознается
по ведущей в него короткой стрелке.
Каждое допускающее состояние отмечается на диаграмме
двойным кружком.
является переходом данного конечного автомата.
Каждое начальное состояние распознается
по ведущей в него короткой стрелке.
Каждое допускающее состояние отмечается на диаграмме
двойным кружком.
Пример 2.1.4. На диаграмме изображен конечный автомат из примера 2.1.2.
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{aaa}
\ar `ur_r{+/u7mm/}`r_dr{[0,2]}^{ab} "1,3"
\ar "1,3" ^{b}
&
& *=[o][F=]{2}
\ar `dl_l{+/d7mm/}`l_ul{[0,-2]}^{\varepsilon} "1,1"
}](/sites/default/files/tex_cache/26d7eff928e8c48fd27971bb0fe90955.png)
Замечание 2.1.5. Если в конечном автомате имеются несколько переходов с общим началом и общим концом, то такие переходы называются параллельными. Иногда на диаграмме состояний конечного автомата параллельные переходы изображают одной стрелкой. При этом метки переходов перечисляют через запятую.
Пример 2.1.6. На диаграмме снова изображен конечный автомат из примера 2.1.2.
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{aaa}
\ar "1,3" <1mm> ^{ab,b}
&
& *=[o][F=]{2}
\ar "1,1" <1mm> ^{\varepsilon}
}](/sites/default/files/tex_cache/1bf41d4ad8a230143b77bbb63df0e14a.png)
Определение 2.1.7. Путь
(path) конечного автомата - это кортеж  ,
где
,
где 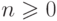 и
и  для каждого i.
При этом q0 - начало пути qn - конец пути n - длина пути w1...wn - метка пути.
для каждого i.
При этом q0 - начало пути qn - конец пути n - длина пути w1...wn - метка пути.
Замечание 2.1.8.
Для любого состояния  существует путь
существует путь  .
Его метка -
.
Его метка -  ,
начало и конец совпадают.
,
начало и конец совпадают.
Определение 2.1.9. Путь называется успешным если его начало принадлежит I, а конец принадлежит F.
Пример 2.1.10.
Рассмотрим конечный автомат из примера 2.1.2.
Путь  является успешным.
Его метка - baaab.
Длина этого пути - 4.
является успешным.
Его метка - baaab.
Длина этого пути - 4.
Определение 2.1.11. Слово w допускается (is accepted, is recognized) конечным автоматом M, если оно является меткой некоторого успешного пути.
Определение 2.1.12. Язык, распознаваемый конечным автоматом M, - это язык L(M), состоящий из меток всех успешных путей (то есть из всех допускаемых данным автоматом слов). Будем также говорить, что автомат M распознает (recognizes, accepts) язык L(M).
Замечание 2.1.13.
Если  ,
то язык, распознаваемый конечным автоматом
,
то язык, распознаваемый конечным автоматом  ,
содержит
,
содержит  .
.
Пример 2.1.14.
Пусть 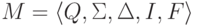 ,
где Q = {1,2},
,
где Q = {1,2}, 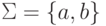 , I = {1}, F = {1,2},
, I = {1}, F = {1,2},
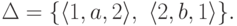
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" <0.6mm> ^{a}
& *=[o][F=]{2}
\ar "1,1" <0.6mm> ^{b}
}](/sites/default/files/tex_cache/bc5170483f2b94c51b54497cdb532412.png)

Определение 2.1.15. Два конечных автомата эквивалентны, если они распознают один и тот же язык.
Определение 2.1.16. Язык L называется автоматным (finite-state language), если существует конечный автомат, распознающий этот язык.
Замечание 2.1.17. Обычно в учебниках используется более узкое определение недетерминированного конечного автомата, но это не меняет класса автоматных языков (см. лемму 2.3.3.).
Пример 2.1.18.
Рассмотрим однобуквенный алфавит  .
При любых фиксированных
.
При любых фиксированных 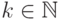 и
и  язык
язык  является автоматным.
является автоматным.
Замечание 2.1.19. Каждый конечный язык является автоматным.
Определение 2.1.20. Состояние q достижимо (reachable) из состояния p, если существует путь, началом которого является p, а концом - q.
Лемма 2.1.21. Каждый автоматный язык распознается некоторым конечным автоматом, в котором каждое состояние достижимо из некоторого начального состояния и из каждого состояния достижимо хотя бы одно заключительное состояние.
Пример 2.1.22.
Рассмотрим конечный автомат  ,
где Q = {1,2,3,4},
,
где Q = {1,2,3,4}, 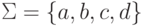 , I = {1,2,4}, F = {1,3,4},
, I = {1,2,4}, F = {1,3,4},

![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
%
& *=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "2,1" _{a}
\ar "2,2" <0.6mm> ^{b}
& *=[o][F=]{3}
\ar "2,2" ^{c}
\\
*=[o][F-]{2}
\ar @`{+/l16mm/} [] ^{}
& *=[o][F=]{4}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" <0.6mm> ^{d}
&
}](/sites/default/files/tex_cache/894fdb56825c1b103b19717e713daafc.png)
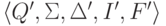 ,
где Q' = {1,4}, I' = {1,4}, F' = {1,4},
,
где Q' = {1,4}, I' = {1,4}, F' = {1,4},
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "2,1" <0.6mm> ^{b}
\\
*=[o][F=]{4}
\ar @`{+/l16mm/} [] ^{}
\ar "1,1" <0.6mm> ^{d}
}](/sites/default/files/tex_cache/56000e2f1edb1abcf86855457cdc66ac.png)
Замечание 2.1.23 Естественным обобщением конечного автомата является конечный преобразователь (finite-state transducer), позволяющий на каждом такте отправить несколько символов в дополнительный "выходной" поток. В некоторых книгах конечными автоматами называют именно такие устройства (с выходным потоком).
В данном пособии конечные преобразователи рассматриваться не будут.
Упражнение 2.1.24. Найти конечный автомат, распознающий язык 
Упражнение 2.1.25. Найти конечный автомат, распознающий язык 
Упражнение 2.1.26. Найти конечный автомат, распознающий язык 
Упражнение 2.1.27. Найти конечный автомат, распознающий язык 
Упражнение 2.1.28. Найти конечный автомат, распознающий язык 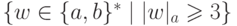
Упражнение 2.1.28. Найти конечный автомат, распознающий язык 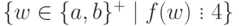 ,
где
,
где 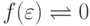 ,
,  и
и  для любого
для любого 
