Машины Тьюринга

Двусторонние исчисления

Оказывается, что рассуждение предыдущего раздела можно немного усилить. Назовем ассоциативное исчисление (е набор правил) двусторонним, если оно вместе с каждым правилом X -> Y содержит и симметричное правило Y -> X.

Теорема 62. Существует двустороннее исчисление, для которого нет алгоритма, выясняющего, можно ли получить одно слово из другого по правилам этого исчисления.

Для доказательства мы воспользуемся той же конструкцией с небольшими изменениями. Для начала правило заменим на правило ]-> (мы вскоре увидим, зачем это нужно). После этого для каждого правила добавим обратное. Это новое исчисление I' также моделирует машину Тьюринга:

Лемма. Двоичное слово Y является результатом работы машины на двоичном слове X тогда и только тогда, когда слово [X] можно преобразовать в слово Y по правилам исчисления I'.

Доказательство леммы. Если не добавлять обратные правила, то I' ничем не отличается от ранее построенного исчисления (кроме последнего шага, где остается звездочка но это, очевидно, несущественно). Поэтому нам надо лишь показать, что если [X] можно преобразовать в слово Y по правилам исчисления I', то это можно сделать без применения обратных правил, только с помощью прямых.

Доказывается это так. Назовем " активными" следующие символы алфавита исчисления I': символ [ (который, напомним, заменяется на первом же шаге), все состояния машины, , , и . Тогда в каждом правиле нашего исчисления слева и справа есть ровно один активный символ. Следовательно, в любой последовательности прямых и обратных правил, соединяющей [X] с Y , все слова содержат по одному активному символу.

Теперь такое наблюдение: к слову, в котором один активный символ, применимо не более одного прямого правила. (Это легко проверить, посмотрев все правила; причина здесь в том, что правила моделируют работу детерминированной машины Тьюринга, в которой следующая конфигурация определена однозначно.) Поэтому можно удалить все обратные правила из последовательности преобразований [X] в Y .

В самом деле, рассмотрим последнее вхождение обратного правила в последовательность преобразований. Оно не может быть самым последним в последовательности, так как обратное правило не порождает символ . Значит, за ним следует применение какого-то прямого правила. Но одно прямое правило, которое можно применить, уже есть это то, к которому было обратно наше обратное правило. В силу единственности другого прямого правила быть не может. Поэтому применение обратного, а за ним прямого правила можно взаимно сократить и получить более короткую последовательность, в которой снова найти последнее обратное правило и т.д. Лемма доказана.

Из нее сразу же следует существование неразрешимых двусторонних ассоциативных исчислений, которое и составляло утверждение основной теоремы этого раздела.

Полугруппы, образующие и соотношения

Сейчас мы объясним, как только что доказанное утверждение о двусторонних ассоциативных исчислениях переводится на алгебраический язык. (Ничего нового по существу при этом не утверждается, это просто перевод.) Напомним некоторые сведения из алгебры.

Полугруппой называется произвольное непустое множество G с ассоциативной операцией, записываемой как умножение, причем существует единичный элемент 1, для которого 1* x =x * 1=x для всех . (Полугруппы без единичного элемента нам не потребуются.) Пусть G некоторая полугруппа. Говорят, что множество является множеством образующих для полугруппы G, если всякий элемент полугруппы может быть получен как произведение образующих (возможно, пустое такое произведение считается равным 1 ). Полугруппа называется конечно порожденной, если она имеет конечное множество образующих.

Пусть A={a₁,...,a_n} алфавит. Тогда множество всех слов в алфавите A образует полугруппу. Умножение в ней это конкатенация слов, то есть приписывание одного к другому. Единичный элемент пустое слово. Очевидно, a₁,...,a_n являются образующими этой полугруппы. (Точнее следовало бы говорить об однобуквенных словах как образующих.) Эта полугруппа называется свободной полугруппой с образующими a₁,...,a_n. Будем обозначать ее F(a₁,...,a_n).

Пусть G произвольная полугруппа, и g₁,...,g_n любые ее элементы. Тогда существует единственный гомоморфизм h полугруппы F(a₁,...,a_n) в полугруппу G, для которого h(a_i)=g_i. ( Гомоморфизмом полугрупп называют отображение, при котором образ произведения равен произведению образов и единица переходит в единицу.) Он переводит слово из символов a_i в произведение соответствующих элементов g_i ; образом пустого слова является единичный элемент. Очевидно, образ этого гомоморфизма совпадает со всей полугруппой G тогда и только тогда, когда элементы g₁,...,g_n являются образующими группы G.

Соотношениями мы будем называть равенства вида X=Y, где X и Y элементы свободной полугруппы F(a₁,...,a_n), то есть слова в алфавите A. Говорят, что соотношение X=Y выполнено в полугруппе G с выделенными элементами g₁,...,g_n, если образы слов X и Y при описанном гомоморфизме, то есть произведения соответствующих элементов g_i, равны. Пусть имеется некоторый набор соотношений X₁=Y₁,...,X_k=Y_k. Будем рассматривать различные полугруппы G с выделенными n элементами, в которых выполнены все эти соотношения, и в которых выделенные элементы являются образующими. (Например, полугруппа из единственного единичного элемента также входит в их число.) Среди таких полугрупп, как мы сейчас увидим, есть " максимальная", в которой выполнено меньше всего соотношений.

Введем на словах алфавита A отношение эквивалентности, считая, что , если P можно преобразовать в Q в двустороннем ассоциативном исчислении с правилами . (Другими словами, в любом слове разрешается заменить его подслово X_i на подслово Y_i и наоборот.) Очевидно, это отношение действительно будет отношением эквивалентности. Заметим, что если , то и для произвольного слова R (в цепочке преобразований можно дописать ко всем словам R слева или справа). Рассмотрим классы эквивалентности этого отношения. На них можно определить операцию произведения, считая произведением двух классов, содержащих слова P и Q, класс, содержащий их конкатенацию PQ. Отмеченное свойство отношения эквивалентности гарантирует корректность этого определения (класс-произведение не зависит от выбора представителей в сомножителях). Тем самым мы получаем полугруппу G, в которой единичным элементом будет класс пустого слова, а классы g_i=[a_i] эквивалентности однобуквенных слов будут образующими. Ее обозначают

F(a1,...,an)/(X1=Y1,...,Xk=Yk)

и называют полугруппой с образующими a₁,...,a_k и соотношениями X₁=Y₁,...,X_k=Y_k. Ясно, что в полугруппе G выполнены исходные соотношения X_i=Y_i. Легко понять также, что в ней нет никаких других соотношений, кроме следствий исходных:

Теорема 63. Если соотношение X=Y выполнено в полугруппе

F(a1,...,an)/(X1=Y1,...,Xk=Yk),

то оно выполнено в любой полугруппе G с выделенными элементами g₁,...,g_n, в которой выполнены все соотношения X_i=Y_i.

В самом деле, словам X и Y соответствуют их классы эквивалентности по описанному отношению, так что из X можно получить Y по правилам двустороннего ассоциативного исчисления. Но все эти правила не меняют значение элемента в любой полугруппе, в которой выполнены соотношения X_i=Y_i, и потому в любой такой полугруппе словам X и Y будет соответствовать один и тот же элемент.

  79. Рассмотрим полугруппу с двумя образующими a₁ и a₂ и соотношениями , 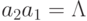. Что это за полугруппа?

  80. Рассмотрим полугруппу с двумя образующими a₁ и a₂ и соотношением a₁a₂=a₂a₁. Что это за полугруппа?

  81. Рассмотрим полугруппу с двумя образующими a₁ и a₂ и соотношениями , , 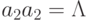a₁a₂=a₂a₁. Что это за полугруппа?

  82. Рассмотрим полугруппу с двумя образующими a₁ и a₂ и соотношениями , , a₁a₂=a₂a₂a₁. Что это за полугруппа?

Теперь мы можем сформулировать утверждение о существовании неразрешимых двусторонних ассоциативных исчислений в терминах полугрупп.

Теорема 64. Существует полугруппа, с конечным числом образующих и конечным числом соотношений, в которой задача проверки равенства двух слов, составленных из образующих, алгоритмически неразрешима (нет алгоритма, который по двум словам такого вида узнавал, равны они в этой полугруппе или не равны).

Согласно определению, равенство двух слов, составленных из образующих, означает возможность преобразовать одно из них в другое по правилам двустороннего исчисления, так что эта теорема представляет собой переформулировку теоремы 62.

Эта теорема была доказана в 1947 году независимо Постом и Андреем Андреевичем Марковым (младшим); вскоре после этого Петр Сергеевич Новиков усилил ее, построив пример группы (а не только полугруппы!) с конечным числом образующих и соотношений, для которой проблема равенства двух слов из образующих неразрешима.