НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 10: Собственные числа и собственные векторы матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3973 / 713 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 62 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Пример 9.19.4.

$\begin{gathe} A = \begin{pmatrix} \phm 0 & 1\\ -1 & 0 \end{pmatrix},\\ p(\lambda)=|A-\lambda E| = \begin{vmatrix} -\lambda & \phm 1\\ -1 & -\lambda \end{vmatrix} = \lambda^2+1. \end{gathe}$

а) K= R : нет действительных корней многочлена $p(\lambda)=\lambda^2+1$ , поэтому для матрицы A нет действительных собственных чисел (и собственных векторов).

б) K= C : многочлен 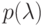$p(\lambda)$ имеет корни $\lambda_1=i\in C$ , $\lambda_2=-i\in C$ (собственные числа матрицы A ).

Собственные векторы для $\lambda=i :$

$\begin{pmatrix} -i & \phm 1\\ -1 & -i \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix},$

ненулевые решения:

$\left\{\left.c\cdot \begin{pmatrix}-i\\\phm 1\end{pmatrix}\right| c\in C,\ c\neq 0\right\}.$

Собственные векторы для $\lambda=-i :$

$\begin{pmatrix} \phm i & 1\\ -1 & i \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix},$

ненулевые решения

$\left\{\left.c\cdot \begin{pmatrix}i\\ 1\end{pmatrix}\right| c\in C,\ c\neq 0\right\}.$

Пример 9.19.5.

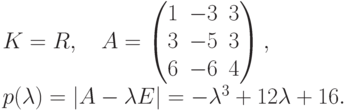
$\begin{gathe} K= R,\quad A= \begin{pmatrix} 1 & -3 & 3\\ 3 & -5 & 3\\ 6 & -6 & 4 \end{pmatrix},\\ p(\lambda)=|A-\lambda E|=-\lambda^3+12\lambda+16. \end{gathe}$

Корни многочлена $p(\lambda) :$ $\lambda_1=-2$ , $\lambda_2=-2$ , $\lambda_3=4$ (собственные числа).

Собственные векторы для $\lambda=-2 :$

$(A+2E) \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix},$

ненулевые решения

$\left\{\left. \begin{pmatrix}s-t\\ s\\ t\end{pmatrix}\right| s,t\in R,\ s^2+t^2\neq 0\right\}.$

Собственные векторы для $\lambda=4 :$

$(A-4E) \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix},$

ненулевые решения

$\left\{\left. \begin{pmatrix}s\\ s\\ 2s\end{pmatrix}\right| s\in R,\ s\neq 0\right\}.$

Задача 9.19.6 (уравнение Сильвестера). Пусть $A\in M_{n}( C)$ , $B\in M_{m}( C)$ , $C\in M_{n,m}( C)$ и матрицы A и B не имеют общих собственных чисел. Тогда матричное уравнение Сильвестера AX-XB=C имеет единственное решение $X\in M_{n,m}( C)$ .

Задача 9.19.7. Пусть $A,B\in M_{n}( C)$ , AB=BA. Покажите, что для матриц A и B существует общий собственный вектор.

Трудная задача 9.19.8. Пусть $A,B\in M_{n}( C)$ и r(AB-BA)=1. Тогда для матриц A и B существует общий собственный вектор.

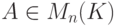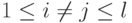Теорема 9.19.9. Пусть $A\in M_{n}(K)$ , $0\neq\hat X_1,...,\hat X_l\in\hat K_n$ , $\lambda_1,...,\lambda_l\in K$ , $\lambda_i\neq\lambda_j$ при $1 \leq i\neq j \leq l$ , $A\cdot \hat X_i=\lambda_i\cdot \hat X_i$ , i=1,...,l. Тогда столбцы $\hat X_1,...,\hat X_l$ линейно независимы, т. е. собственные векторы, отвечающие различным собственным значениям, линейно независимы.

Доказательство. Доказательство проведем индукцией по l. Основание индукции: l=1, $A\cdot\hat X_1=\lambda_1\cdot\hat X_1$ , $0\neq\hat X_1$ , $\{\hat X_1\}$ - линейно независимая система векторов.

Пусть теперь $l \geq 2$ и наше утверждение доказано для всех l', $1 \leq l'<l$ .Допустим, что

$\begin{equation}\label{triestelo} \alpha_1\hat X_1+...+\alpha_l \hat X_l=0\in\hat K^n,\quad \alpha_i\in K,\quad i=1,...,l. \end{equation}$

( 9.6)

Умножая слева на матрицу A обе части равенства, получаем, что

$\alpha_1\cdot A\cdot \hat X_1+...+\alpha_l\cdot A\cdot \hat X_l= A\cdot 0=0\in\hat K^n,$

и поэтому

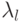$\begin{equation}\label{triedusteloj} \alpha_1\lambda_1 \hat X_1+...+\alpha_l\lambda_l \hat X_l=0. \end{equation}$

( 9.7)

Умножая (9.6) на $\lambda_l$ , имеем

$\begin{equation}\label{tristeloj} \alpha_1\lambda_l\hat X_1+...+\alpha_l\lambda_l \hat X_l=0. \end{equation}$

( 9.8)

Вычитаем (9.8) из (9.7):

$\begin{equation*} \alpha_1(\lambda_1-\lambda_l)\hat X_1+...+ \alpha_{l-1}(\lambda_{l-1}-\lambda_l) \hat X_{l-1}=0\in \hat K^n. \end{equation*}$

Применяя предположение индукции, получаем, что

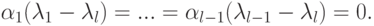
$\alpha_1(\lambda_1-\lambda_l)=...= \alpha_{l-1}(\lambda_{l-1}-\lambda_l) =0.$

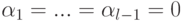Поскольку $\lambda_1\neq\lambda_l$ ,..., $\lambda_{l-1}\neq\lambda_l$ , отсюда следует, что $\alpha_1=...=\alpha_{l-1}=0$ . Следовательно, из (9.6) следует, что 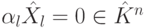$\alpha_l\hat X_l=0\in \hat K^n$ . Так как $\hat X_l\neq 0$ , то $\alpha_l=0$ . Таким образом, $\alpha_1=...=\alpha_l=0$ , и поэтому собственные векторы $\hat X_1,...,\hat X_l$ линейно независимы.

Следствие 9.19.10. Если 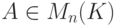$A\in M_n(K)$ , характеристический многочлен p(t)=|A-tE| имеет n различных корней $\lambda_1,...,\lambda_n$ в поле K, то матрица A подобна диагональной матрице:

$C^{-1}AC=d(\lambda_1,...,\lambda_n),\ \ \text{где}\ \ C\in\GL_n(K).$

Теорема 9.19.11. Матрица 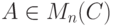$A\in M_n( C)$ нильпотентна (т. е. $A^m=0\in M_n(K)$ для некоторого $m\in N$ ) тогда и только тогда, когда собственные числа $\lambda_1,...,\lambda_n$ равны нулю.

Доказательство.

а) Если $\lambda_1=\lambda_2=...=\lambda_n=0$ , то $|A-\lambda E|=(-1)^n\lambda^n$ . По теореме Гамильтона Кэли $A^n=(0)\in M_n( C)$ .

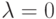б) Если $A^m=(0)\in M_n( C)$ и $A\hat X=\lambda\hat X$ , где $\lambda\in C$ , $0\neq\hat X\in\hat{ C}^n$ , то $\hat{ C}^n\ni 0=A^m\hat X=\lambda^n\hat X$ , следовательно, $\lambda^n=0$ и $\lambda=0$ .

Замечание 9.19.12. Одним из фундаментальных результатов об алгебре матриц M_n( C) над полем комплексных чисел C (и о строении отдельно взятого линейного оператора конечномерного линейного пространства _CV ) является теорема о жордановой нормальной форме:

для каждой матрицы 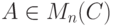$A\in M_n( C)$ найдется такая обратимая матрица $C\in\GL_n( C)$ , что
$C^{-1}AC=J_A= \left(\begin{array}{c|c|c|c} J_1 & 0 & ... & 0\\ \hline 0 & J_2 & ... & 0\\ \hline & & \vdots & \\ \hline 0 & 0 & & J_k \end{array} \right) \text{ -}$
жорданова матрица (т. е. J₁,...,J_k - жордановы клетки, см. упражнение 8.6.8);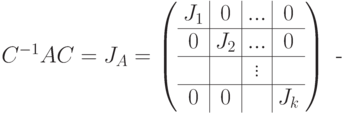
нормальная жорданова форма J_A матрицы A определена однозначно (с точностью до порядка жордановых клеток).

Эта теорема обычно является одним из центральных результатов курса линейной алгебры. Она также доказывается в более общем виде в разделе о строении конечнопорожденных модулей над кольцами главных идеалов.

Конечно, теорема Гамильтона Кэли над полем C$ является следствием теоремы о жордановой нормальной форме. В то же время имеются элегантные доказательства теоремы о жордановой нормальной форме, использующие теорему Гамильтона Кэли.

Мы оставляем этот сюжет для следующих частей наших "начал алгебры" (или его можно рассматривать как достаточно трудную задачу).

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Собственные числа и собственные векторы матрицы

Вопросы и ответы