Линейные подпространства линейных пространств
Линейные подпространства линейных пространств
Пусть K - поле, K V - линейное пространство над полем K. Непустое подмножество 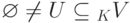 называется линейным подпространством линейного пространства K V, если:
называется линейным подпространством линейного пространства K V, если:
-
 для всех
для всех 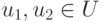 ;
; -
 для всех
для всех 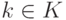 ,
, 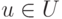 .
.
Ясно, что K U - линейное пространство относительно тех же операций сложения элементов и умножения на элементы из поля K, что и в линейном пространстве K V.
Если U - линейное подпространство в конечномерном линейном пространстве KV, 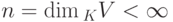 , то
, то  . Действительно, если элементы
. Действительно, если элементы  линейно независимы в K U, то эти элементы линейно независимы и в линейном пространстве K V,
линейно независимы в K U, то эти элементы линейно независимы и в линейном пространстве K V,  , поэтому
, поэтому  .
.
Если K U - линейное подпространство линейного пространства K V,  и
и  , то K U=K V. Действительно, если {u1,...,un} - базис линейного пространства
, то K U=K V. Действительно, если {u1,...,un} - базис линейного пространства  , то эти n элементов u1,...,un линейно независимы в K V и
, то эти n элементов u1,...,un линейно независимы в K V и  , поэтому {u1,...,un} - базис линейного пространства K V. Итак, каждый элемент
, поэтому {u1,...,un} - базис линейного пространства K V. Итак, каждый элемент  имеет вид
имеет вид  ,
,  , т. е. K V=K U.
, т. е. K V=K U.
Пересечение линейных подпространств
Лемма 9.11.1. Пересечение
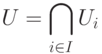
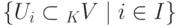 линейного пространства K V является линейным подпространством.
линейного пространства K V является линейным подпространством.Доказательство. Если  ,
, 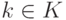 , то
, то  для любого
для любого  , поэтому
, поэтому 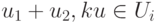 для любого
для любого  , т. е.
, т. е.  .
.
Следствие 9.11.2. Если U1 и U2 - линейные подпространства линейного пространства K V, то  - линейное подпространство в {K V (наибольшее подпространство среди подпространств, лежащих одновременно в U1 и в U2 ).
- линейное подпространство в {K V (наибольшее подпространство среди подпространств, лежащих одновременно в U1 и в U2 ).
Сумма линейных подпространств
Если U1 и U2 - линейные подпространства линейного пространства K V, то сумма линейных подпространств
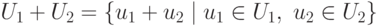
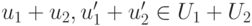 ,
, 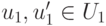 ,
, 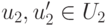 ,
, 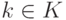 , то
, то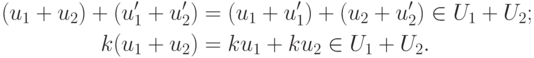
Замечание 9.12.1. U1+U2 - наименьшее линейное подпространство среди линейных подпространств, содержащих одновременно U1 и U2. Более того,

Замечание 9.12.2. Если U, U1, U2, U3 - линейные подпространства в K V, то
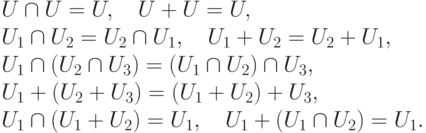
Линейная оболочка элементов линейного пространства
Пусть K V - линейное пространство,  . Рассмотрим
. Рассмотрим

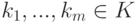 , называемую линейной оболочкой элементов v1,...,vm. Линейная оболочка
, называемую линейной оболочкой элементов v1,...,vm. Линейная оболочка 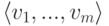 является наименьшим линейным подпространством, содержащим элементы v1,...,vm. Действительно,
является наименьшим линейным подпространством, содержащим элементы v1,...,vm. Действительно,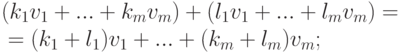
 , то
, то 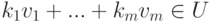 , следовательно,
, следовательно,  . Более того,
. Более того,
Замечание 9.13.1. Если  , то
, то  ,
,  ; если v=0,
; если v=0,  .
.
Замечание 9.13.2.  .
.
Замечание 9.13.3.  ; любая максимальная линейно независимая подсистема в {v1,...,vm} является базисом линейного подпространства
; любая максимальная линейно независимая подсистема в {v1,...,vm} является базисом линейного подпространства 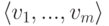 .
.
Основная лемма о линейной зависимости может быть сформулирована в следующей эквивалентной форме.
Теорема 9.13.4 (о замене). Пусть 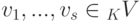 - линейно независимая система,
- линейно независимая система,  , {u1,...,ur} - линейно независимая система элементов. Тогда
, {u1,...,ur} - линейно независимая система элементов. Тогда  и
и
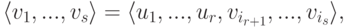
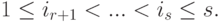
Доказательство. Так как  , то
, то  . Если r=s, то
. Если r=s, то  . Если r<s, то найдется
. Если r<s, то найдется  (индекс ir+1 - минимальный с этим свойством). Продолжая этот процесс, построим базис
(индекс ir+1 - минимальный с этим свойством). Продолжая этот процесс, построим базис 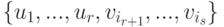 в
в  .
.
Следствие 9.13.5. Пусть U, W - линейные подпространства в K V и 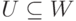 ,
, 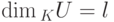 ,
,  . Тогда
. Тогда  и любой базис подпространства U можно дополнить m-l элементами до базиса подпространства W. В частности, если
и любой базис подпространства U можно дополнить m-l элементами до базиса подпространства W. В частности, если 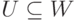 и l=m, то U=W.
и l=m, то U=W.
Теорема 9.13.6 (формула размерности). Пусть U, W - линейные подпространства в K V,  . Тогда
. Тогда
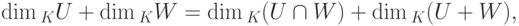
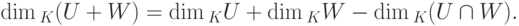
Доказательство. Пусть 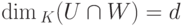 ,
,  ,
,  . Ясно, что
. Ясно, что 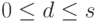 ,
,  . При d=0 утверждение очевидно (объединение базисов в U и W дает базис в U+W ). Выберем базис v1,...,vd линейного пространства
. При d=0 утверждение очевидно (объединение базисов в U и W дает базис в U+W ). Выберем базис v1,...,vd линейного пространства  и дополним его до базиса v1,...,vd,u1,...,us-d линейного пространства U и до базиса v1,...,vd,w1,...,wt-d линейного пространства W. Ясно, что
и дополним его до базиса v1,...,vd,u1,...,us-d линейного пространства U и до базиса v1,...,vd,w1,...,wt-d линейного пространства W. Ясно, что
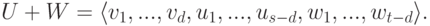

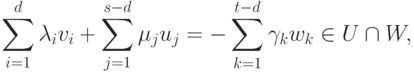
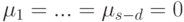 ,
, 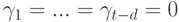 . Следовательно,
. Следовательно,  . Таким образом,
. Таким образом,
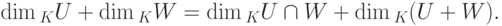
Теорема 9.13.7 (о существовании прямого дополнения подпространства). Пусть  , U - линейное подпространство в K V. Тогда существует линейное подпространство W в K V такое, что
, U - линейное подпространство в K V. Тогда существует линейное подпространство W в K V такое, что
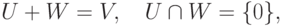
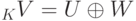 ).
).Доказательство. Если 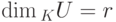 и {u1,...,ur} - базис в K U, то дополним его до базиса линейного пространства K V: u1,...,ur,v1,...,vn-r. Пусть
и {u1,...,ur} - базис в K U, то дополним его до базиса линейного пространства K V: u1,...,ur,v1,...,vn-r. Пусть  . Тогда K V=U+W,
. Тогда K V=U+W,  .
.
Замечание 9.13.8. Конечно, прямое дополнение определено неоднозначно, однако все прямые дополнения линейного пространства изоморфны (а именно, все они имеют размерность  ).
).
Замечание 9.13.9. Если 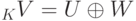 , то представление элемента
, то представление элемента  в виде v=u+w,
в виде v=u+w, 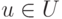 ,
,  , определено однозначно (действительно, если v=u+w=u'+w',
, определено однозначно (действительно, если v=u+w=u'+w',  ,
,  , то
, то  , следовательно, u=u', w=w' ), и поэтому линейное пространство
, следовательно, u=u', w=w' ), и поэтому линейное пространство  изоморфно \emph{внешней прямой} сумме
изоморфно \emph{внешней прямой} сумме  линейных пространств K U и K W с естественными операциями сложения пар и их умножения на
линейных пространств K U и K W с естественными операциями сложения пар и их умножения на  .
.
Пример 9.13.10 (прямого разложения). Пусть
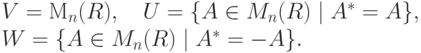
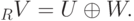
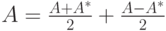 . Если A=A*=-A, то
. Если A=A*=-A, то  .
.