НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 1: Определители и их свойства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3973 / 713 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 62 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматривается понятие определителя матрицы и связанные с этим понятием определения. Вводится понятие линейной комбинации строк и транспонированной матрицы. Приведены примеры решения задач, а также упражнения для самостоятельного решения

Ключевые слова: определитель, матрица, поле, подстановка, доказательство, Произведение, отношение, разбиение

Определители малых порядков

Рассматривая систему линейных уравнений

$\left\{ \begin{array}{@{}l@{}} a_{11}x_1+a_{12}x_2=b_1,\\ a_{21}x_1+a_{22}x_2=b_2, \end{array} \right.$

для вычисления x₁ умножим первое уравнение на a₂₂, второе уравнение на -a₁₂ и сложим их. Получим (a₁₁a₂₂-a₁₂a₂₁)x₁=b₁a₂₂-b₂a₁₂. Аналогично, для вычисления x₂ умножим первое уравнение на -a₂₁, второе уравнение на a₁₁ и сложим их. Получим (a₁₁a₂₂-a₁₂a₂₁)x₂=a₁₁b₂-a₂₁b₁. Если мы определителем $(2\times 2)$ -матрицы

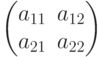
$\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix}$

назовем число

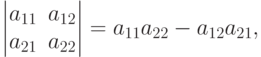
$\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22}-a_{12}a_{21},$

то в этом частном случае мы получим следующее утверждение (правило Крамера для n=2 ): если определитель квадратной системы отличен от нуля, т. е.

$\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22}-a_{12}a_{21}\neq 0,$

то система является определенной и для ее единственного решения справедливы формулы

$x_1 = \frac{\begin{vmatrix} b_1 & a_{12}\\ b_2 & a_{22} \end{vmatrix}}% {\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix}},\quad x_2=\frac{\begin{vmatrix} a_{11} & b_1\\ a_{21} & b_2 \end{vmatrix}}% {\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix}}.$

Непосредственная проверка показывает, что (x₁,x₂) - решение.

Упражнение 6.1.1. Проделать аналогичную процедуру в случае n=3.

Замечание 6.1.2. Очевидно, что определители второго порядка обладают следующими свойствами:

$\begin{alignat*}{2} & 1) &\quad &\begin{vmatrix} 1 & 0\\ 0 & 1 \end{vmatrix} = 1; \\[0.5\baselineskip] & 2) &&\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = - \begin{vmatrix} a_{21} & a_{22}\\ a_{11} & a_{12} \end{vmatrix}; \\[0.5\baselineskip] & 3) &&\begin{vmatrix} ca_{11} & ca_{12}\\ a_{21} & a_{22} \end{vmatrix} = c \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix}, \intertext{аналогично для второй строки;} & 4) && \text{если } (a_{11},a_{12}) = (b_1,b_2)+(c_1,c_2), \text{ то} \\ &&& \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = \begin{vmatrix} b_1 & b_2\\ a_{21} & a_{22} \end{vmatrix} + \begin{vmatrix} c_1 & c_2\\ a_{21} & a_{22} \end{vmatrix}, \intertext{аналогично для второй строки;} & 5) && \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = \begin{vmatrix} a_{11} & a_{21}\\ a_{12} & a_{22} \end{vmatrix}. \end{alignat*}$

Наша ближайшая цель - построить общую теорию определителей квадратных $(n\times n)$ -матриц и привести многочисленные приложения определителей, в частности в системах линейных уравнений.

Отметим, что на начальном периоде теория определителей формировалась параллельно с аксиоматической теорией площадей и объемов. Например, в декартовой системе координат на плоскости определитель

$\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}$

равен (ориентированной) площади параллелограмма, построенного на векторах (a₁₁,a₁₂) и (a₂₁,a₂₂).

Определители квадратных n x n -матриц

Пусть

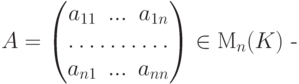
$A = \begin{pmatrix} a_{11} & ... & a_{1n}\\ \hdotsfor{3}\\ a_{n1} & ... & a_{nn} \end{pmatrix} \in \mM_n(K) \text{ - }$

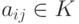квадратная $(n\times n)$ -матрица, $a_{ij}\in K$ , где K - любое поле (например, K= R ).

При n=1 : $|a|=a\in K$ .

При n=2 мы имеем

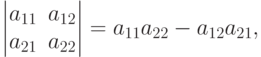
$\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22}-a_{12}a_{21},$

т. е. определитель $(2\times 2)$ -матрицы является суммой двух слагаемых, каждое из которых является произведением элементов матрицы, взятых по одному (и только одному) из каждой строки (столбца), при этом знак определяется четностью соответствующей подстановки индексов:

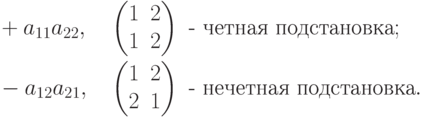
$\begin{alignat*}{2} & +a_{11}a_{22}, &\quad & \begin{pmatrix} 1 & 2\\ 1 & 2 \end{pmatrix} \text{ - четная подстановка};\\ & -a_{12}a_{21}, && \begin{pmatrix} 1 & 2\\ 2 & 1 \end{pmatrix} \text{ - нечетная подстановка}. \end{alignat*}$

С этой "подсказкой" определим определитель квадратной матрицы A как

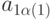$|A|=\sum_{\alpha\in S_n} \varepsilon(\alpha) a_{1\alpha(1)}... a_{n\alpha(n)},$

т. е. как сумму всех произведений элементов матрицы A, взятых по одному (и только одному) из каждой строки и каждого столбца ( $a_{1\alpha(1)}$ - из 1 -й строки и $\alpha(1)$ -го столбца; $a_{n\alpha(n)}$ - из n -й строки и $\alpha(n)$ -го столбца), т. е. тех произведений, индексы которых дают подстановку $\alpha\in S_n$ , при этом эти произведения берутся со знаком + ( $\varepsilon(\alpha)=1$ ), если подстановка $\alpha$ четная, и со знаком - ( $\varepsilon(\alpha)=-1$ ), если подстановка $\alpha$ нечетная.

Упражнение 6.2.1. Если n=3, $A=(a_{ij})\in\mM_3(K)$ , то

$\begin{mult} |A|=a_{11}a_{22}a_{33}+a_{13}a_{21}a_{32}+a_{12}a_{23}a_{31}-{} \\ {}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}. \end{mult}$

Мнемоническое правило: три произведения

входят со знаком + ; три произведения

входят со знаком -.

Упражнение 6.2.2. При n=3, $A=(a_{ij})\in\mM_3( R)$ в декартовой системе координат в R³ определитель |A| матрицы A равен ориентированному объему параллелепипеда, построенного на векторах (a₁₁,a₁₂,a₁₃), (a₂₁,a₂₂,a₂₃) и (a₃₁,a₃₂,a₃₃).

Упражнение 6.2.3. Если $A=(a_{ij})\in \mM_3( R)$ , то все шесть слагаемых в разложении определителя третьего порядка |A| одновременно не могут быть положительны.

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Определители и их свойства

Определители малых порядков

Определители квадратных n x n -матриц

Вопросы и ответы