НОУ ИНТУИТ | Основы теории нечетких множеств. Лекция 2: Нечеткие отношения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.07.2006 | Доступ: свободный | Студентов: 3071 / 549 | Оценка: 4.00 / 3.77 | Длительность: 15:27:00

ISBN: 978-5-94774-818-5

Темы: Алгоритмы и дискретные структуры, Искусственный интеллект и робототехника

Специальности: Программист, Математик

|

Вам нравится? Нравится 35 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Проекции нечетких отношений

Важную роль в теории нечетких множеств играет понятие проекции нечеткого отношения. Дадим определение проекции бинарного нечеткого отношения.

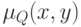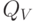Пусть $\mu_{Q}(x,y)$ — функция принадлежности нечеткого отношения в ${U\times V}$ . Проекции $Q_{U}$ и $Q_{V}$ отношения на и 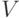— есть множества в и 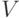с функцией принадлежности вида

$\begin{gathered} \mu _{Q_U } (x) = \mathop {\sup }\limits_V \;\mu _Q (x,y), \\ \mu _{Q_V } (y) = \mathop {\sup }\limits_U \;\mu _Q (x,y). \\ \end{gathered}$

Условной проекцией нечеткого отношения на , при произвольном фиксированном $y_{0}\in V$ , называется множество $P_{U}$ с функцией принадлежности вида $\mu _{P_U } (x|y_0 ) = \mu _Q (x,y_0 )$ .

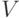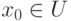Аналогично определяется условная проекция на при заданном $x_{0}\in U$ :

$\mu _{P_V } (y|x_0 ) = \mu _Q (x_0 ,y).$

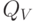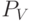Из данного определения видно, что проекции $Q_{U}$ и $Q_{V}$ не влияют на условные проекции $P_{U}$ и $P_{V}$ , соответственно. Дадим далее определение, которое учитывает их взаимосвязь.

Условные проекции второго типа определяются следующим образом:

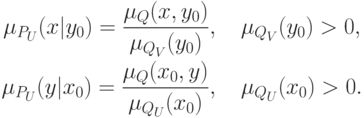
$\begin{gathered} \mu _{P_U } (x|y_0 ) = \frac{{\mu _Q (x,y_0 )}} {{\mu _{Q_V } (y_0 )}},\quad \mu _{Q_V } (y_0 ) > 0, \\ \mu _{P_U } (y|x_0 ) = \frac{{\mu _Q (x_0 ,y)}} {{\mu _{Q_U } (x_0 )}},\quad \mu _{Q_U } (x_0 ) > 0. \\ \end{gathered}$

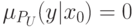Если $\mu _{Q_V } (y_0 ) = 0$ или $\mu _{Q_U } (x_0 ) = 0$ , то полагаем, соответственно, что $\mu _{P_U } (x|y_0 ) = 0$ или $\mu _{P_U } (y|x_0 ) = 0$ .

Заметим, что условные проекции первого типа содержатся в соответствующих проекциях второго типа.

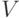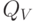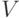Пусть и — базовые множества, — нечеткое отношение в $U\times V$ и $Q_{U}$ и $Q_{V}$ — его проекции на и , соответственно.

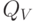Нечеткие множества $Q_{U}$ и $Q_{V}$ называются независимыми, если

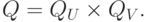
$Q= Q_{U}\times Q_{V}.$

Следовательно, они независимы по первому типу, если

$\mu _Q (x,y) = \mu _{Q_U } (x) \wedge \mu _{Q_V } (y),$

и независимы по второму типу, если

$\mu _Q (x,y) = \mu _{Q_U } (x) \cdot \mu _{Q_V } (y).$

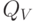В противном случае проекции $Q_{U}$ и $Q_{V}$ являются зависимыми (соответствующего типа).

Независимость второго типа можно интерпретировать следующим образом. Данные соотношения с учетом производильности 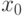$x_{0}$ и $u_{0}$ перепишем в виде

$\begin{gathered} \mu _Q (x,y) = \mu _{P_U } (x|y)\mu _{Q_V^{} } (y), \\ \mu _Q (x,y) = \mu _{P_V } (y|x)\mu _{Q_U^{} } (x). \\ \end{gathered}$

Дальше >>

Авторизоваться

Основы теории нечетких множеств

Нечеткие отношения

Проекции нечетких отношений

Вопросы и ответы