Типизация
Ковариантность и скрытие потомком
Если бы мир был прост, то разговор о типизации можно было бы и закончить. Мы определили цели и преимущества статической типизации, изучили ограничения, которым должны соответствовать реалистичные системы типов, и убедились в том, что предложенные методы типизации отвечают нашим критериям.
Но мир не прост. Объединение статической типизации с некоторыми требованиями программной инженерии создает проблемы более сложные, чем это кажется с первого взгляда. Проблемы вызывают два механизма: ковариантность (covariance) - смена типов параметров при переопределении, скрытие потомком (descendant hiding) - способность класса потомка ограничивать статус экспорта наследуемых компонентов.
Ковариантность
Что происходит с аргументами компонента при переопределении его типа? Это важнейшая проблема, и мы уже видели ряд примеров ее проявления: устройства и принтеры, одно- и двухсвязные списки и т. д. (см. разделы 16.6, 16.7).
Вот еще один пример, помогающий уяснить природу проблемы. И пусть он далек от реальности и метафоричен, но его близость к программным схемам очевидна. К тому же, разбирая его, мы будем часто возвращаться к задачам из практики.
Представим себе готовящуюся к чемпионату лыжную команду университета. Класс GIRL включает лыжниц, выступающих в составе женской сборной, BOY - лыжников. Ряд участников обеих команд ранжированы, показав хорошие результаты на предыдущих соревнованиях. Это важно для них, поскольку теперь они побегут первыми, получив преимущество перед остальными. (Это правило, дающее привилегии уже привилегированным, возможно и делает слалом и лыжные гонки столь привлекательными в глазах многих людей, являясь хорошей метафорой самой жизни.) Итак, мы имеем два новых класса: RANKED_GIRL и RANKED_BOY.
Для проживания спортсменов забронирован ряд номеров: только для мужчин, только для девушек, только для девушек-призеров. Для отображения этого используем параллельную иерархию классов: ROOM, GIRL_ROOM и RANKED_GIRL_ROOM.
Вот набросок класса SKIER:
class SKIER feature
roommate: SKIER
-- Сосед по номеру.
share (other: SKIER) is
-- Выбрать в качестве соседа other.
require
other /= Void
do
roommate := other
end
... Другие возможные компоненты, опущенные в этом и последующих классах ...
endНас интересуют два компонента: атрибут roommate и процедура share, "размещающая" данного лыжника в одном номере с текущим лыжником:
s1, s2: SKIER ... s1.share (s2)
При объявлении сущности other можно отказаться от типа SKIER в пользу закрепленного типа like roommate (или like Current для roommate и other одновременно). Но давайте забудем на время о закреплении типов (мы к ним еще вернемся) и посмотрим на проблему ковариантности в ее изначальном виде.
Как ввести переопределение типов? Правила требуют раздельного проживания юношей и девушек, призеров и остальных участников. Для решения этой задачи при переопределении изменим тип компонента roommate, как показано ниже (здесь и далее переопределенные элементы подчеркнуты).
class GIRL inherit
SKIER
redefine roommate end
feature
roommate: GIRL
-- Сосед по номеру.
endПереопределим, соответственно, и аргумент процедуры share. Более полный вариант класса теперь выглядит так:
class GIRL inherit
SKIER
redefine roommate, share end
feature
roommate: GIRL
-- Сосед по номеру.
share (other: GIRL) is
-- Выбрать в качестве соседа other.
require
other /= Void
do
roommate := other
end
endАналогично следует изменить все порожденные от SKIER классы (закрепление типов мы сейчас не используем). В итоге имеем иерархию:
Так как наследование является специализацией, то правила типов требуют, чтобы при переопределении результата компонента, в данном случае roommate, новый тип был потомком исходного. То же касается и переопределения типа аргумента other подпрограммы share. Эта стратегия, как мы знаем, именуется ковариантностью, где приставка "ко" указывает на совместное изменение типов параметра и результата. Противоположная стратегия называется контравариантностью.
Все наши примеры убедительно свидетельствуют о практической необходимости ковариантности.
- Элемент односвязного списка LINKABLE должен быть связан с другим подобным себе элементом, а экземпляр BI_LINKABLE - с подобным себе. Ковариантно переопределяется и аргумент в put_right.
- Всякая подпрограмма в составе LINKED_LIST с аргументом типа LINKABLE при переходе к TWO_WAY_LIST потребует аргумента BI_LINKABLE.
- Процедура set_alternate принимает DEVICE -аргумент в классе DEVICE и PRINTER -аргумент - в классе PRINTER.
Ковариантное переопределение получило особое распространение потому, что скрытие информации ведет к созданию процедур вида
set_attrib (v: SOME_TYPE) is
-- Установить attrib в v.
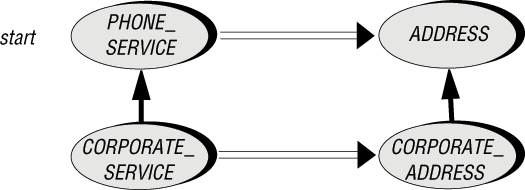
...для работы с attrib типа SOME_TYPE. Подобные процедуры, естественно, ковариантны, поскольку любой класс, который меняет тип атрибута, должен соответственно переопределять и аргумент set_attrib. Хотя представленные примеры укладываются в одну схему, но ковариантность распространена значительно шире. Подумайте, например, о процедуре или функции, выполняющей конкатенацию односвязных списков (LINKED_LIST). Ее аргумент должен быть переопределен как двусвязный список (TWO_ WAY_LIST). Универсальная операция сложения infix "+" принимает NUMERIC -аргумент в классе NUMERIC, REAL - в классе REAL и INTEGER - в классе INTEGER. В параллельных иерархиях телефонной службы процедуре start в классе PHONE_SERVICE может требоваться аргумент ADDRESS, представляющий адрес абонента, (для выписки счета), в то время как этой же процедуре в классе CORPORATE_SERVICE потребуется аргумент типа CORPORATE_ADDRESS.
Что можно сказать о контравариантном решении? В примере с лыжниками оно означало бы, что если, переходя к классу RANKED_GIRL, тип результата roommate переопределили как RANKED_GIRL, то в силу контравариантности тип аргумента share можно переопределить на тип GIRL или SKIER. Единственный тип, который не допустим при контравариантном решении, - это RANKED_GIRL! Достаточно, чтобы возбудить наихудшие подозрения у родителей девушек.
Параллельные иерархии
Чтобы не оставить камня на камне, рассмотрим вариант примера SKIER с двумя параллельными иерархиями. Это позволит нам смоделировать ситуацию, уже встречавшуюся на практике: TWO_ WAY_LIST > LINKED_LIST и BI_LINKABLE > LINKABLE ; или иерархию с телефонной службой PHONE_SERVICE.
Пусть есть иерархия с классом ROOM, потомком которого является GIRL_ROOM (класс BOY опущен):
Наши классы лыжников в этой параллельной иерархии вместо roommate и share будут иметь аналогичные компоненты accommodation (размещение) и accommodate (разместить):
indexing
description: "Новый вариант с параллельными иерархиями"
class SKIER1 feature
accommodation: ROOM
accommodate (r: ROOM) is ... require ... do
accommodation:= r
end
endЗдесь также необходимы ковариантные переопределения: в классе GIRL1 как accommodation, так и аргумент подпрограммы accommodate должны быть заменены типом GIRL_ROOM, в классе BOY1 - типом BOY_ROOM и т.д. (Не забудьте: мы по-прежнему работаем без закрепления типов.) Как и в предыдущем варианте примера, контравариантность здесь бесполезна.
Своенравие полиморфизма
Не довольно ли примеров, подтверждающих практичность ковариации? Почему же кто-то рассматривает контравариантность, которая вступает в противоречие с тем, что необходимо на практике (если не принимать во внимание поведения некоторых молодых людей)? Чтобы понять это, рассмотрим проблемы, возникающие при сочетании полиморфизма и стратегии ковариантности. Придумать вредительскую схему несложно, и, возможно, вы уже создали ее сами:
s: SKIER; b: BOY; g: GIRL ... create b; create g;-- Создание объектов BOY и GIRL. s := b; -- Полиморфное присваивание. s.share (g)
Результат последнего вызова, вполне возможно приятный для юношей, - это именно то, что мы пытались не допустить с помощью переопределения типов. Вызов share ведет к тому, что объект BOY, известный как b и благодаря полиморфизму получивший псевдоним s типа SKIER, становится соседом объекта GIRL, известного под именем g. Однако вызов, хотя и противоречит правилам общежития, является вполне корректным в программном тексте, поскольку share-экспортируемый компонент в составе SKIER, а GIRL, тип аргумента g, совместим со SKIER, типом формального параметра share.
Схема с параллельной иерархией столь же проста: заменим SKIER на SKIER1, вызов share - на вызов s.accommodate (gr), где gr - сущность типа GIRL_ROOM. Результат - тот же.
При контравариантном решении этих проблем не возникало бы: специализация цели вызова (в нашем примере s) требовала бы обобщения аргумента. Контравариантность в результате ведет к более простой математической модели механизма: наследование - переопределение - полиморфизм. Данный факт описан в ряде теоретических статей, предлагающих эту стратегию. Аргументация не слишком убедительна, поскольку, как показывают наши примеры и другие публикации, контравариантность не имеет практического использования.
| В литературе для программистов нередко встречается призыв к методам, основанных на простых математических моделях. Однако математическая красота - всего лишь один из критериев ценности результата, - есть и другие - полезность и реалистичность. |
Поэтому, не пытаясь натянуть контравариантную одежду на ковариантное тело, следует принять ковариантную действительность и искать пути устранения нежелательного эффекта.
Скрытие потомком
Прежде чем искать решение проблемы ковариантности, рассмотрим еще один механизм, способный в условиях полиморфизма привести к нарушениям типа. Скрытие потомком (descendant hiding) - это способность класса не экспортировать компонент, полученный от родителей.
Типичным примером является компонент add_vertex (добавить вершину), экспортируемый классом POLYGON, но скрываемый его потомком RECTANGLE (ввиду возможного нарушения инварианта - класс хочет оставаться прямоугольником):
class RECTANGLE inherit
POLYGON
export {NONE} add_vertex end
feature
...
invariant
vertex_count = 4
endНе программистский пример: класс "Страус" скрывает метод "Летать", полученный от родителя "Птица".
Давайте на минуту примем эту схему такой, как она есть, и поставим вопрос, будет ли легитимным сочетание наследования и скрытия. Моделирующая роль скрытия, подобно ковариантности, нарушается из-за трюков, возможных из-за полиморфизма. И здесь не трудно построить вредоносный пример, позволяющий, несмотря на скрытие компонента, вызвать его и добавить прямоугольнику вершину:
p: POLYGON; r: RECTANGLE ... create r; -- Создание объекта RECTANGLE. p := r; -- Полиморфное присваивание. p.add_vertex (...)
Так как объект r скрывается под сущностью p класса POLYGON, а add_vertex экспортируемый компонент POLYGON, то его вызов сущностью p корректен. В результате выполнения в прямоугольнике появится еще одна вершина, а значит, будет создан недопустимый объект.