Тензоры: опыт создания пользовательского пакета программ
Отметим, что сама команда замены координат имеет вид
changeBas[<номер исходного базиса>,<номер целевого базиса>]
После ее успешного выполнения значения компонент тензоров возвращаются в целевом базисе. Если же выполнить замену не удалось, что бывает, если матрицы (функции) перехода не заданы и не могут быть вычислены внутри программы, то выдается сообщение, предлагающее задать необходимые матрицы (функции).
Дифференциальные формы: их разложение по базису, внешнее умножение и дифференцирование. В настоящий момент в пакете реализован ряд возможностей для работы с дифференциальными формами. Как уже упоминалось выше, можно задать кососимметрический тензор или тензорное поле типа (0,q) с помощью команд makeSkew, makeSkewTab или makeSkewField:
![In[118] := resetTensors ;
\\
makeBasisDif[x, 5] ;
\\
makeSkew[\xi , 3 ] ;
\\
makeSkew[\zeta , 2 ] ;](/sites/default/files/tex_cache/3089cc3662b1157f5e31e49452b2d15b.png)
Дифференциальную форму можно разложить по базису. Дифференциальные формы также можно перемножить внешним образом (как описанные выше кососимметрические тензоры):
![In[121] := toBasisSkew[\xi ]
\\
toBasisSkew[\xi ^ \zeta ]](/sites/default/files/tex_cache/31871885d624032c7bee25cd78e5c84b.png)
![Out[121]=\begin{matrix}\\\xi\\123\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}2\\dx\\\end{matrix}\wedge \begin{matrix}3\\dx\\\end{matrix}+\begin{matrix}\\\xi\\124\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}2\\dx\\\end{matrix}\wedge \begin{matrix}4\\dx\\\end{matrix}+\begin{matrix}\\\xi\\125\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}2\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}+\\
\qquad \qquad \begin{matrix}\\\xi\\134\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}3\\dx\\\end{matrix}\wedge \begin{matrix}4\\dx\\\end{matrix}+\begin{matrix}\\\xi\\135\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}3\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}+\begin{matrix}\\\xi\\145\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}4\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}+\\
\qquad\qquad \begin{matrix}\\\xi\\234\end{matrix}\begin{matrix}2\\dx\\\end{matrix}\wedge\begin{matrix}3\\dx\\\end{matrix}\wedge \begin{matrix}4\\dx\\\end{matrix}+\begin{matrix}\\\xi\\235\end{matrix}\begin{matrix}2\\dx\\\end{matrix}\wedge\begin{matrix}3\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}+\begin{matrix}\\\xi\\245\end{matrix}\begin{matrix}2\\dx\\\end{matrix}\wedge\begin{matrix}4\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}+\begin{matrix}\\\xi\\345\end{matrix}\begin{matrix}3\\dx\\\end{matrix}\wedge\begin{matrix}4\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}\\
Out[122]=\\
\left(\begin{matrix}&\\\zeta&\xi\\45&123\end{matrix}-\begin{matrix}&\\\zeta&\xi\\35&124\end{matrix}+\begin{matrix}&\\\zeta&\xi\\34&125\end{matrix}+\begin{matrix}&\\\zeta&\xi\\25&134\end{matrix}-\begin{matrix}&\\\zeta&\xi\\24&135\end{matrix}+\begin{matrix}&\\\zeta&\xi\\23&145\end{matrix}-\begin{matrix}&\\\zeta&\xi\\15&234\end{matrix}+\begin{matrix}&\\\zeta&\xi\\14&235\end{matrix}-\begin{matrix}&\\\zeta&\xi\\13&245\end{matrix}+\begin{matrix}&\\\zeta&\xi\\12&345\end{matrix}\right)\\
\qquad \begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}2\\dx\\\end{matrix}\wedge \begin{matrix}3\\dx\\\end{matrix}\wedge \begin{matrix}4\\dx\\\end{matrix}\wedge\begin{matrix}5\\dx\\\end{matrix}](/sites/default/files/tex_cache/0b7756d4055e46f9a2fdbb4549c443c9.png)
Можно задать форму с коэффициентами-функциями:
![In[123] := resetTensors ;
\\
makeBasisDif[x, 3] ;
\\
makeSkewField[\omega , 1 ] ;
\\
toBasisSkew[\omega ]](/sites/default/files/tex_cache/009fde5635f9a093aed02f8794a737ea.png)
![Out[126]=\begin{matrix}1\\dx\\\end{matrix}\begin{matrix}\\\omega\\1\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\\&&\end{matrix}\right]+\begin{matrix}2\\dx\\\end{matrix}\begin{matrix}\\\omega\\2\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\\&&\end{matrix}\right]+\begin{matrix}3\\dx\\\end{matrix}\begin{matrix}\\\omega\\3\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\\&&\end{matrix}\right]](/sites/default/files/tex_cache/a7984da37169b420e1d9ae075dd99f96.png)
От такой формы можно взять внешний дифференциал, который, как и положено, будет дифференциальной формой:
![In[127] := toBasisSkew [d [\omega ] ]](/sites/default/files/tex_cache/f4fcb78c9e30b242b1edc97a7ec105d5.png)
![Out[127]=\begin{matrix}2\\dx\\\end{matrix}\wedge \begin{matrix}3\\dx\\\end{matrix}
\left(\begin{matrix}\\-\omega ^{(0,0,0)}\\2\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\end{matrix}\right]+\begin{matrix}\\\omega ^{(0,1,0)}\\3\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\end{matrix}\right]\right)+
\qquad \begin{matrix}1\\dx\\\end{matrix}\wedge \begin{matrix}2\\dx\\\end{matrix}
\left(\begin{matrix}\\-\omega ^{(0,1,0)}\\1\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\end{matrix}\right]+\begin{matrix}\\\omega ^{(1,0,0)}\\2\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\end{matrix}\right]\right)+\\
\qquad \begin{matrix}1\\dx\\\end{matrix}\wedge \begin{matrix}3\\dx\\\end{matrix}
\left(\begin{matrix}\\-\omega ^{(0,0,1)}\\1\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\end{matrix}\right]+\begin{matrix}\\\omega ^{(1,0,0)}\\3\end{matrix}\left[\begin{matrix}1&2&3\\x,&x,&x\end{matrix}\right]\right)](/sites/default/files/tex_cache/8f61550435e35707309f81a62b5b88d8.png)
Можно задать форму непосредственно, как вот такую форму P:
![In[128]:=makeDasisDif[x,5];\\
\begin{matrix}
&&&&P=Cos\left[\begin{matrix}1\\x\\\end{matrix}\right]\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}2\\dx\\\end{matrix}\wedge\begin{matrix}3\\dx\\\end{matrix}+Sin\left[\begin{matrix}3\\x\\\end{matrix}\right]\begin{matrix}2\\dx\\\end{matrix}\wedge\begin{matrix}4\\dx\\\end{matrix}+\begin{matrix}4\\x\\\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge \begin{matrix}2\\dx\\\end{matrix}\wedge \begin{matrix}5\\dx\\\end{matrix}+\begin{matrix}5^2\\x\\\end{matrix}\begin{matrix}1\\dx\\\end{matrix}\wedge\begin{matrix}3\\dx\\\end{matrix}\wedge \begin{matrix}4\\dx\\\end{matrix} \end{matrix};](/sites/default/files/tex_cache/e10f4121b5a8d84623241eeec104e910.png)
От нее тоже можно взять внешний дифференциал:
In[130]:=d[P]
![Out[130]=Cos\left[\begin{matrix}3\\x\\\end{matrix}\right]\begin{matrix}1\\dx\\\end{matrix} \wedge \begin{matrix}2\\dx\\\end{matrix} \wedge \begin{matrix}3\\dx\\\end{matrix} \wedge \begin{matrix}4\\dx\\\end{matrix}+\begin{matrix}1\\dx\\\end{matrix} \wedge \begin{matrix}2\\dx\\\end{matrix} \wedge \begin{matrix}4\\dx\\\end{matrix} \wedge \begin{matrix}5\\dx\\\end{matrix}-2 \begin{matrix}5\\x\\\end{matrix}\begin{matrix}1\\dx\\\end{matrix} \wedge \begin{matrix}3\\dx\\\end{matrix}\wedge\begin{matrix}4\\dx\\\end{matrix}\wedge\begin{matrix}5\\dx\\\end{matrix}](/sites/default/files/tex_cache/964680e85456830f1180cb4d3672d360.png)
однако ни P, ни d[P], в этом случае не являются тензорами:
In[131] := tensor [P]
skew[P]
tensor[d[P] ]
tensorBas[P]
skewBas[P]
tensorBas[d[P]]
skewBas[d[P]]
Out[131] = False
Out[132] = False
Out[133] = False
Out[134l = True
Out[135] = True
Out[136] = True
Out[137] = TrueПревратить их в тензорное поле можно так:
In[138]:=makeSkewTab[dP, toListSkew [d[P] ] ]
tensor[dP]
dP
{1,2,3,4}
Out[139] = True![Out[140]=Cos\left[\begin{matrix}3\\x\\\end{matrix}\right]](/sites/default/files/tex_cache/00bde5777c48f323df3d5cf7b4935d8d.png)
Риманова метрика, риманова и аффинная связности. В пакете предусмотрена возможность объявить рассматриваемое многообразие (в текущей версии, напомним, многообразие состоит из одной карты) римановым. При этом задается или
- абстрактная метрика g и обратный тензор ig (команда makeRiemann ), или
- метрика с конкретной матрицей (команда makeRiemannTab[<матрица>] ).
В обоих случаях для метрики и обратного тензора зарезервированы символы g и ig :
In[141] := resetTensors ;
makeBasisDif[{х, у}];
makeRiemann;
Пакет Tensors перезапущен. Результаты вычислений аннулированы.
Созданы метрические тензоры д типа (0,2) и ig типа (2,0)
In[144] :=Row [ {val [g] //MatrixForm, val[ig] //MatrixForm} ,
Spacer[10]]![Out[144]=\begin{pmatrix}
g&g\\
11&12\\
g&g\\
12&22
\end{pmatrix}\begin{pmatrix}
11&12\\
ig&ig\\
12&22\\
ig&ig
\end{pmatrix}](/sites/default/files/tex_cache/4b76d4dee67c5149ecef5f17c35bf644.png)
Отметим, что оба построенных тензора по определению симметричны. Аналогично:
In[145] := resetTensors ;
makeBasisDif[{х, у}] ;![\begin{matrix}
&&&makeRiemannTab \left[ \begin{pmatrix}1&0\\0&1\end{pmatrix}\right];
\end{matrix}](/sites/default/files/tex_cache/d64dbd2c9df0ed240add653ad79fdcf0.png)
val[g] //MatrixForm
Пакет Tensors перезапущен. Результаты вычислений аннулированы.
Создан метрический тензор g типа
(0,2) и обратный к нему тензор ig типа (2,0)![Out[148]=\begin{pmatrix}1&0\\
0&1
\end{pmatrix}](/sites/default/files/tex_cache/0739cc07a61282a9e44e15e9edf82d4e.png)
При этом, конечно, метрика - это тензор, компоненты которого пересчитывают при замене координат. Так, например, можно вычислить компоненты евклидовой метрики в полярных координатах:
![In[149]:=makeBasisDif [\{ r, \varphi \} , \{ r Cos[\varphi ], r Sin[\varphi ]\} ];
\\
val[g] //MatrixForm](/sites/default/files/tex_cache/3bae53ff360f58cbba90c2e685d52756.png)
![Out[150]=\begin{pmatrix}
1&0\\
0&r^2
\end{pmatrix}](/sites/default/files/tex_cache/28a175847476f0bbdcadbf8b34f5d086.png)
Если задана метрика, то можно вычислить символы Кристоффеля соответствующей симметричной римановой связности, что делается с помощью команды makeCrRiemann . Для символов Кристоффеля зарезервирована буква ? (большая греческая буква гамма, Esc G Esc ). При этом с символами Кристоффеля во многом можно обращатьсякак с тензорами типа (1,2), а именно, можно посмотреть конкретную компоненту, можно вычислять их значение в текущих координатах с помощью все той же функции val :
In[151] := resetTensors ;
makeBasisDif[{х, у, z}];![\begin{matrix}
&&&makeRiemannTab \left[ \begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}\right];
\end{pmatrix}](/sites/default/files/tex_cache/41736ceacc68b4f6cea120e240b1b3ef.png)
makeCrRiemann
val[Г]
Пакет Tensors перезапущен. Результаты вычислений аннулированы.
Создан метрический тензор g типа
(0,2) и обратный к нему тензор ig типа (2,0)
Out[155]={{{0, 0, 0}, {0, 0, 0}, {0, 0, 0}},
{{0, 0, 0}, {0, 0, 0}, {0, 0, 0}},
{{0, 0, 0}, {0, 0, 0}, {0, 0, 0}}}Мы вычислили символы Кристоффеля евклидовой связности, которые, разумеется, равны нулю. Пересчитаем их теперь, скажем, в цилиндрических координатах:
![In[156] := makeBasisDif [ \{ r, \varphi , z\} , \{ r Cos[\varphi ], r Sin[\varphi ] , z\} ];
\\
val[Г]
\\
\\
Out[157]=\{ \{ \{ 0, 0, 0\} , \{ 0, -r, 0\} , \{ 0, 0, 0\} \} ,
\\
\{ \{ 0, 1/r, 0\} , \{ 1/r, 0, 0\} , \{ 0, 0, 0\} \} ,
\\
\{ \{ 0, 0, 0\} , \{ 0, 0, 0\} , \{ 0, 0, 0\} \} \}](/sites/default/files/tex_cache/965707bccd0d68a59d2928f6a1bff0a0.png)
Или вот конкретная компонента:
![In[158]:=\begin{matrix}\{1\}\\Г\\\{2,2\}\end{matrix}\\
Out[158] = - r](/sites/default/files/tex_cache/a5f86da55eb0eb042980285f5f603540.png)
Кроме того, предусмотрена возможность задавать абстрактную аффинную связность. При этом соответствующие функции
makeCrAffine[]
и
makeCrAffineTab[<таблица значений>>]
можно использовать как без явного указания имени связности (в этом случае ей присваивается имя Г), так и с указанием этого имени в виде последнего аргумента:
In[159] =makeCrAf f ine [ ] ;
val[r]![Out[160]=\left\{\left\{\left\{\begin{matrix}1&1&1\\Г,&Г,&Г\\11&12&13\end{matrix}\right\},\left\{\begin{matrix}1&1&1\\Г,&Г,&Г\\21&22&23\end{matrix}\right\},\left\{\begin{matrix}1&1&1\\Г,&Г,&Г\\ 31&32&33\end{matrix}\right\}\right\},\\](/sites/default/files/tex_cache/b0f89d54d89e277b4b323927583cd32a.png)
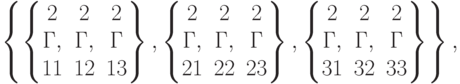
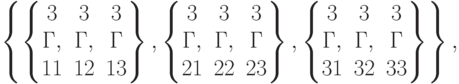
In[161] :=makeCrAf fine [AA] ;
val[AA]![Out[162]=\left\{\left\{\left\{\begin{matrix}1&1&1\\АА,&АА,&АА\\11&12&13\end{matrix}\right\},\left\{\begin{matrix}1&1&1\\АА,&АА,&АА\\21&22&23\end{matrix}\right\},\left\{\begin{matrix}1&1&1\\АА,&АА,&АА\\ 31&32&33\end{matrix}\right\}\right\},\\](/sites/default/files/tex_cache/27f7d87b3592d064bafe2fe81293c103.png)
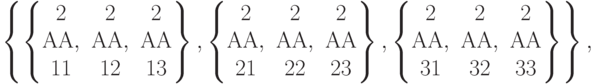
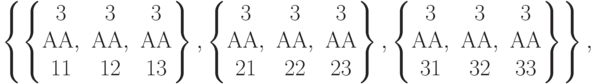
![In[163]:=makeCrAffineTab[val[AA]];\\
\begin{matrix}
&&&&\begin{matrix}\{1\}\\Г\\\{3,2\}\end{matrix}
\end{matrix}\\
Out[164]=\begin{matrix}1\\AA\\32\end{matrix}\\
In[165]:=makeCrAffineTab[val[AA], BB];\\
\begin{matrix}
&&&&\begin{matrix}\{3\}\\BB\\\{2,1\}\end{matrix}
\end{matrix}\\
Out[166]=\begin{matrix}3\\AA\\21\end{matrix}](/sites/default/files/tex_cache/28e4d06795cb99fc4fdd1787c8b2833f.png)
Наконец, имеется возможность задавать метрику как тензорное поле. В этом случае компоненты метрики суть абстрактные функции от координат. Аналогичная возможность предусмотрена и для абстрактной аффинной связности. Соответствующие функции - это makeRiemannField , которая создает поля g и ig , makeCrAffineField[], которая создает связность Г , и makeCrAffineField[<имя связности>] , которая создает связность с заданным именем:
In[167] := resetTensors ;
makeBasisDif[x, 2] ;
makeRiemannField;
makeCrRiemann;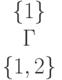
Пакет Tensors перезапущен. Результаты вычислений аннулированы.
Созданы метрические тензорные
поля д типа (0,2) и ig типа (2,0)![Out[171]=\frac12 \begin{matrix}11\\ig\\\end{matrix}\left[\begin{matrix}1&2\\x,&x\\\end{matrix}\right]\begin{matrix}\\g\\11\end{matrix}^{(0,1)}\left[\begin{matrix}1&2\\x,&x\\\end{matrix}\right]+\frac12\begin{matrix}12\\ig\\\end{matrix}\left[\begin{matrix}1&2\\x,&x\\\end{matrix}\right]\begin{matrix}\\g\\22\end{matrix}^{(1,0)}\left[\begin{matrix}1&2\\x,&x\\\end{matrix}\right]\end{matrix}](/sites/default/files/tex_cache/4ad6ba1ec163561dfd7f3c8cae727251.png)
Как работает пакет (краткое описание основных идей)
В этом разделе мы кратко опишем основные идеи и технические приемы, положенные в основу написания пакета. Сами тексты программ находятся в файле tensors.m. Этот файл тоже можно открыть в Mathematica (откройте). Возникнет специальным образом оформленное окно работы с пакетными файлами. Как и любой пакет, наш начинается оператором BeginPackage["Tensors'", {"Combinatorica'","GraphUtilities'"}], где первый аргумент - это имя пакета, а второй - список используемых пакетов, и заканчивается оператором EndPackage[].
В нашем пакете всего две клетки, первая состоит из команд вида <имя функции>::usage="текст описания.", служащих для описания пользовательских функций. Именно этот текст появляется на экране при выполнении команды ?<имя функции> . Если имеется несколько одноименных функций, то будут выведены все описания. Наконец, по команде ??<имя функции> на экран выводится весь код, задающий функцию:
In[172] := ? makeBasis
In[173] := ?? makeTensor
makeTensor [Т , р Integer, q Integer] : =
![\begin{matrix}
&&\left(val[T]=Array\left[\begin{matrix}
StringJoin@@ToString/@\{##1\}[[Range[p] ]]\\
ToString[T]\\
StringJoin@@ToString/@\{##1\}[[Range[p+1, p+q] ]]
\end{matrix} &,
\end{matrix}](/sites/default/files/tex_cache/8245088d2985e714ad4978ee0afdf6a8.png)
ConstantArray[nn[basis[curBas]], p + q] ;
tensor[T] = True; type[T] = {p, q}; inBasis[T] = curBas;
If[TrueQ[symm[T]], (symm[T]) = . ] ;
If[TrueQ[skew[T] ] , (skew[T]) =.];
If[p=0&&q <= l, symm[T] = True; skew[T] = True] ;)Полный список функций пакета можно увидеть, если кликнуть в кнопку Functions в окне работы с файлом пакета.


