Графы в компьютерной геометрии
Пример оптимизационной задачи: задача коммивояжера
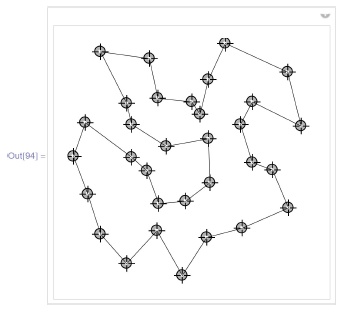
Также очень популярной является так называемая задача коммивояжера, состоящая в том, чтобы найти замкнутый маршрут наименьшего веса, проходящий через все вершины данного взвешенного графа. Одним из ее естественных приложений является поиск оптимального маршрута бродячего торговца (коммивояжера), которому надо объехать данный набор городов и вернуться домой, оптимизируя расходы на дорогу. В настоящее время эффективный точный алгоритм поиска решения этой задачи неизвестен (вероятнее всего, такого алгоритма не существует). В Mathematica реализован ряд приближенных методов решения задачи о коммивояжере, дающих точный ответ для малого числа вершин. Соответствующая функция называется FindShortestTour. По умолчанию весовая функция - евклидово расстояние, а граф - полный:
In [94] :=
Manipulate[
Graphics [
Line [р[[# ≈ Join ≈ {#[[1]]} & @ Last [FindShortestTour [p] ]] ] ] ,
PlotRange -> {{-2, 2}, {-2, 2}}] ,
{{p, {{0, 1}, {1, 0}, {1, 1}}}, Locator,
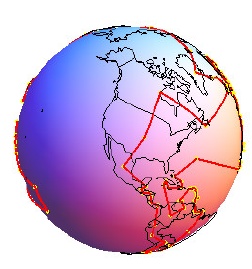
LocatorAutoCreate -> True} ]Снова пользуясь географическими базами данных, можно получить, например, такую картинку, описывающую оптимальный маршрут посещения всех стран мира:
Задача о ближайших соседях и триангуляция Делоне
С помощью триангуляции Делоне и диаграммы Вороного также легко решается, например, известная задача о ближайших соседях. А именно, ближайшими соседями точки  из подмножества
из подмножества 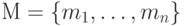 метрического пространства называются такие точки
метрического пространства называются такие точки 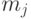 , что
, что  для всех
для всех 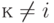 . Можно определить ориентированный граф ближайших соседей, в котором ориентированные ребра, выходящие из вершины
. Можно определить ориентированный граф ближайших соседей, в котором ориентированные ребра, выходящие из вершины 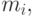 приходят в ближайших соседей
приходят в ближайших соседей 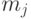 ,- точки
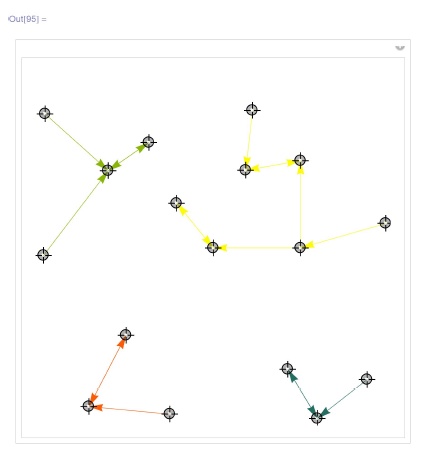
,- точки  . Этот граф, очевидно, также является подграфом триангуляции Делоне. Граф ближайших соседей используется, например, в задачах кластеризации, т. е. разбиения точек множества М на подмножества, составленные, в некотором смысле, из "близких" точек. Один из подходов состоит в выделении компонент слабой связности графа ближайших соседей (ориентированный граф наз
ывается слабо связным, если связен соответствующий ему неориентированный граф):
. Этот граф, очевидно, также является подграфом триангуляции Делоне. Граф ближайших соседей используется, например, в задачах кластеризации, т. е. разбиения точек множества М на подмножества, составленные, в некотором смысле, из "близких" точек. Один из подходов состоит в выделении компонент слабой связности графа ближайших соседей (ориентированный граф наз
ывается слабо связным, если связен соответствующий ему неориентированный граф):
In [95] :=
DynamicModule[{pts, pts0, neibs},
pts0 = {{-1, -1}, {1, 0}, {0, 0}, {0, 1}, {1, 1}};
Manipulate[neibs = FromOrderedPairs[adLists[pts]];
Show[showOrGr[neibs, pts], PlotRange -> { { - 2 , 2}, {-2, 2}}],
{{pts, pts0}, Locator, LocatorAutoCreate -> True}],
Initialization:-> (Needs["Combinatorica""] ;
Needs["ComputationalGeometry' "];
showOrGr[g_, v_] :=
Module[{cmp}, cmp = WeaklyConnectedComponents[g] ;
Graphics[GraphicsComplex[ v,
{ColorData[3, "ColorList"] [[
Mod [Position [cmp, #[[1]] ] [[1, 1]], 10] + 1] ,
Arrow[#]}&/@ Edges[g] ]]];
nearNeib[pts_, i_] := Module [ {delauney, min, dist} ,
delauney = #[[2]] & /@ DelaunayTriangulation [pts] ;
dist = Norm [pts[[i]] - pts[[#]] ] & /@ delauneyjij ;
min = Min[dist] ;
delauney[[i, Flatten[Position[dist, min] ] ]] ] ;
adLists[pts_] : =
Module[{nb, f},
nb = nearNeib [pts, #] &/@ Range [Length [pts] ] ;
f [x_, y_] := {x, #} &/@y;
Flatten[MapThread[f, {Range[Length[pts]], nb}] , 1]])]Минимальные деревья Штейнера
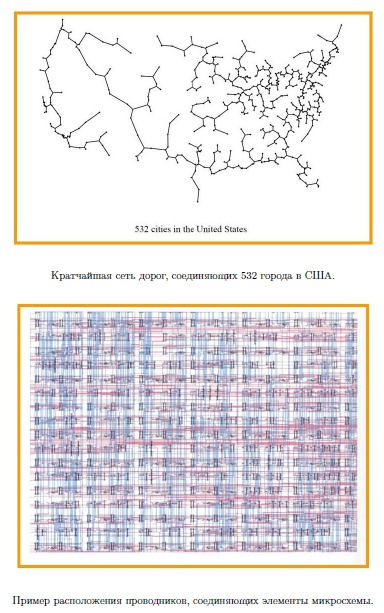
Еще один пример оптимизационной задачи - знаменитая проблема Штейнера. На практике такая задача возникает при проектировании коммуникационных сетей, например, сети дорог, связывающей данные населенные пункты, или сети проводников, соединяющих различные элементы микросхемы. Обычно требуется, чтобы полученная сеть была оптимальна, скажем, имела наименьшую возможную длину. Похожую задачу мы уже разбирали, говоря о минимальном остовном дереве, однако теперь разрешается добавлять промежуточные развилки,что существенно осложняет дело. Эти развилки обычно называют точками Торричелли или точками Штейнера.
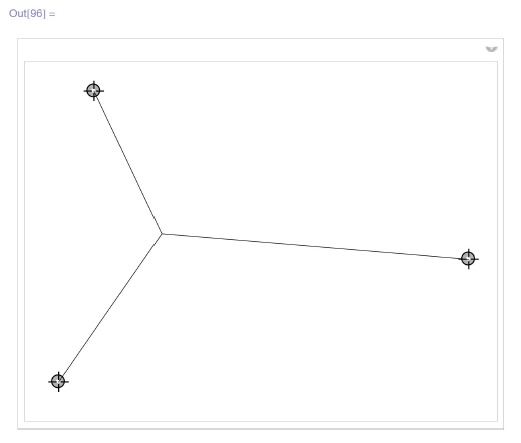
Простейший вариант проблемы Штейнера известен как задача Ферма: построить на евклидовой плоскости такую точку, чтобы суммарное расстояние от нее до заданных трех точек, называемых терминалами, была наименьшей возможной. Ниже приведена визуализация решения этой задачи, причем терминалы задаются локаторами. Поэкспериментируйте с положением локаторов и попробуйте сформулировать определяющее свойство полученной сети:
In [96] : =
Manipulate[Module[{х, у, s},
s=
{х, у} /.
Las t@Quiet@FindMinimum [Plus @@ (Norm[{x, y} - #] & /@p) ,
{{x, First©Mean[p]} , {y, Last@Mean[p]}} ,
Method -> "PrincipalAxis"];
Graphics [Line [{s, #}] &/@p, PlotRange -> { {-2, 2}, {-1, 2}},
AspectRatio -> Automatic] ] ,
{{p, {{-1, 0}, {1, 0}, {0, 1}}}, Locator}]Внимательное изучение поведения сети показывает, что пока все три отрезка невырождены, углы между ними равны между собой и, значит, равны  , а когда один из отрезков вырождается, то угол между оставшимися отрезками не становится меньше, т.е. остается больше или равен
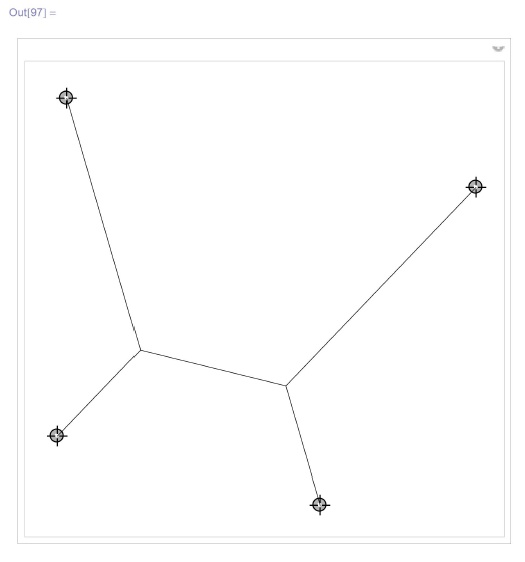
, а когда один из отрезков вырождается, то угол между оставшимися отрезками не становится меньше, т.е. остается больше или равен  . Кроме того, дополнительные вершины не могут иметь степень 1 или 2. На самом деле это действительно так, причем даже в общем случае. Ниже приведен пример кратчайшей сети для четырех терминалов, как на плоскости, так и в трехмерном пространстве:
. Кроме того, дополнительные вершины не могут иметь степень 1 или 2. На самом деле это действительно так, причем даже в общем случае. Ниже приведен пример кратчайшей сети для четырех терминалов, как на плоскости, так и в трехмерном пространстве:
In [97] : = Manipulate [
Module {gl, g2, g3, g, xl, yl, x2, y2, min, res, resl, gr, sub, v,
e, st, dist, MyShowGraph},![\begin{matrix}
&&dist[v_{-}, w_{-}] : = \sqrt{(v - w) . (v - w)} ;
\end{matrix}](/sites/default/files/tex_cache/71dbfa1d931f93a21c2c7bba92b82450.png)
st[gr_, ls_] : =
Quiet@Module [ {w, ее, len} , vv = Vertices [g] ; ее = Edges[g] ;
len = Plus @@ (dist @@ vv[[#]] & /@ ее) ;
FindMinimum [ len, {#, RandomReal [ ] } & /@ Flatten[vv[[ls]]] ,
Method -> "PrincipalAxis"] ≈ Join ≈ {g}] ;
MyShowGraph[g_, opts : OptionsPattern[Graphics]] :=
Module[{vv, ее} , vv = Vertices[g]; ее = Edges[g] ;
Graphics [Line [vv[#] ] &/@ ee, opts]] ;
gl = Graph[{{{l, 5}}, {{2, 5}}, {{5, 6}}, {{6, 3}}, {{6, 4}}},
({#} S/вр) ≈ Join ≈{{{xl, yl}}, {{x2, y2}}}];
g2 = Graph[{{{l, 5}}, {{3, 5}}, {{5, 6}}, {{6, 2}}, {{6, 4}}},
({#} S/ep) ≈ Join ≈{{{xl, yl}}, {{x2, y2}}}] ;
g3 = Graph[{{{l, 5}}, {{4, 5}}, {{5, 6}}, {{6, 3}}, {{6, 2}}},
({#} S/вр) ≈ Join ≈{{{xl, yl}}, {{x2, y2}}}] ;
g = {gl, g2, g3};
res = st[*f, {5, 6}] &/@g;
min = Min[#|[l]] & /@res] ;
resl = Select [res, #|[1]] == min &] // First;
gr = resl // Last;
sub = reslI2J; v = Vertices[gr] / . sub;
e = Edges [gr] ;
MyShowGraph [AddEdges [AddVertices [EmptyGraph [0] , v] , e] ,
PlotRange -> {{-2, 2}, {-2, 2}}]
],
{{p, {{-1, 1}, {-1, -1}, {1, -1}, {1, 1}}}, Locator},
Initialization : -> (
Needs["Combinatoricav"];
)
]