Графы в компьютерной геометрии
Построение графов из уже имеющихся
Имеется много команд, позволяющих менять уже заданный граф. Вот лишь некоторые из них: AddEdge, AddEdges, AddVertex, AddVertices, DeleteEdge, DeleteEdges, MakeDirected, MakeUndirected, DeleteVertex, ReverseEdges, RemoveMultipleEdges и т. д. (полный список команд содержится в Help, в разделе Constructing Graphs ).
In[58] :=ShowGraphArray[{gll, AddEdges [gll, {{2, 5}, {2, 4}}],
g21, AddEdges [g21, {{2, 5}, {2, 4}}]}]In [59]:=
gg = DeleteVertex [gll, 1] ; ggl = AddVertex [gg] ;
gg2 = AddEdges[AddVertex[gg] , {{6, 1}, {6, 2}, {6, 3}, {6, 4}}];
GraphicsRow [Framed /@ ShowGraph /@ {gg, ggl, gg2} ]В этом же разделе Constructing Graphs описаны некоторые операции над графами, способы порождать случайные графы и деревья (см. определение ниже).
Отметим, что, по-видимому, авторы пакета Combinatorica предполагали, вместо непосредственного задания графов, использовать именно построение их из уже имеющихся. Поэтому операции над графами хорошо разработаны и, кроме того, имеется как богатая коллекция встроенных графов, см. Built-in Graphs, так и огромная база GraphData:
In [61] := Manipulate [If [SameQ [h, RandomGraph] , ShowGraph [h [n, 0.5]] ,
ShowGraph[h[n]]],
{{h, EmptyGraph} , {EmptyGraph -> "Пустой", Wheel -> "Колесо",
CompleteGraph -> "Полный" , Hypercube -> "Гиперкуб" ,
RandomGraph -* "Случайный"} , Setter} ,
{{n, 3}, Drop[Range[7] , 2] , PopupMenu} ]Пример оптимизационной задачи: задача о кратчайших путях
Маршрутом 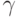 в графе G = (V, E) называется такая последовательность вида
в графе G = (V, E) называется такая последовательность вида  , где
, где  и
и  , что для каждого
, что для каждого  , ребро
, ребро  соединяет вершину
соединяет вершину  с вершиной
с вершиной  . При этом удобно говорить, что маршрут
. При этом удобно говорить, что маршрут 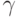 соединяет вершины
соединяет вершины  и
и 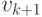 , и называть такой маршрут
, и называть такой маршрут  - маршрутом. Маршрут называется путем, если все его элементы, кроме, быть может,
- маршрутом. Маршрут называется путем, если все его элементы, кроме, быть может,  и
и 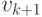 , различны. Путь, в котором
, различны. Путь, в котором  , называется циклом Граф называется связным, если для каждых двух его различных вершин
, называется циклом Граф называется связным, если для каждых двух его различных вершин  и
и 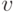 существует (
существует ( 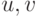 )-маршрут.
)-маршрут.
Пусть  - ориентированный граф. Говорят, что вершина
- ориентированный граф. Говорят, что вершина  достижима из
достижима из  , если существует некоторый (u, v ) -маршрут.
, если существует некоторый (u, v ) -маршрут.
Пусть G = (V, E) - взвешенный граф (ориентированный или нет) весовая функция. Весом маршрута называется сумма весов всех входящих в него ребер. Предположим, что вершина  достижима из
достижима из  , и рассмотрим множество
, и рассмотрим множество 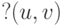 всех (u, v ) -маршрутов в G. Маршрут
всех (u, v ) -маршрутов в G. Маршрут 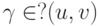 называется кратчайшим путем, если его вес не превосходит веса любого другого маршрута из ?(u,v) . Оказывается, если весовая функция
называется кратчайшим путем, если его вес не превосходит веса любого другого маршрута из ?(u,v) . Оказывается, если весовая функция 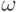 неотрицательна, то существуют полиномиальные (порядка
неотрицательна, то существуют полиномиальные (порядка 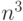 , где n - количество вершин) алгоритмы поиска кратчайшего пути. В Mathematica реализован известные алгоритмы Dijkstra (для положительных весов), а также BellmanFord (для любых весов). Имеется несколько возможностей использования этих алгоритмов. Чтобы проиллюстрировать это, мы воспользуемся сначала генера
тором случайных графов и случайных весов ребер:
, где n - количество вершин) алгоритмы поиска кратчайшего пути. В Mathematica реализован известные алгоритмы Dijkstra (для положительных весов), а также BellmanFord (для любых весов). Имеется несколько возможностей использования этих алгоритмов. Чтобы проиллюстрировать это, мы воспользуемся сначала генера
тором случайных графов и случайных весов ребер:
In [62] : = g : = SetEdgeWeights [ RandomGraph [ 17 , . 2 , Type -> Directed] ] ;
SG[g_] := Module [{gg, el},
gg = g;
el = Edges[gg, EdgeWeight] ;
ShowGraph[SetEdgeLabels[gg, #[[2]] &/@el] ,
EdgeLabel -> True, EdgeLabelColor -> Green,
VertexLabel -> True, VertexLabelColor -> Red]
];
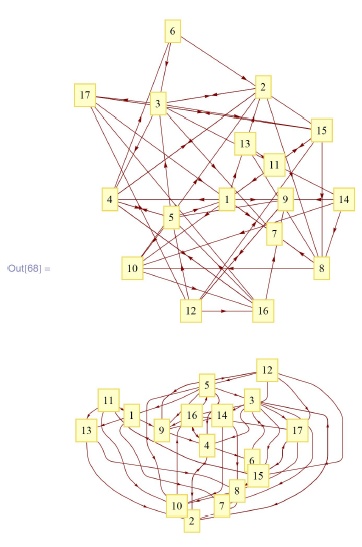
In [64] :=gcur = g;
SG[gcur]Отметим, что такая визуализация не очень наглядна. Ниже мы предложим другие картинки, а пока прокомментируем, как работают нужные нам функции.
Команда ShortestPath[<граф>,<начальная вершина>, <конечная вершина>] выдает кратчайший путь в виде списка последовательных вершин:
In [66] :=sp = ShortestPath[gcur, 1, #] &/@ Drop [Range [17] , 1]
Out[66] =
{{1, 13, 2}, {1, 13, 2, 3}, {1, 9, 4}, {1, 9, 4, 5},
{1, 9, 4, 6}, {1, 7}, {1, 13, 8}, {1, 9}, {1, 13, 8, 10},
{1, 9, 4, 6, 15, 11}, {1, 9, 12}, {1, 13}, {1, 13, 2, 3, 14},
{1, 9, 4, 6, 15}, {1, 13, 8, 10, 16}, {1, 9, 4, 6, 15, 17}}Команда Dijkstra[<взвешенный граф>,<вершина>] ищет кратчайшие пути из заданной вершины во все остальные и выдает дерево, составленное из этих кратчайших путей, а также список весов этих путей. Если вершина недостижима, вес пути равен  . Дерево задано списком, на i -м месте которого стоит номер предшественника i -й вершины на ее кратчайшем пути:
. Дерево задано списком, на i -м месте которого стоит номер предшественника i -й вершины на ее кратчайшем пути:
In[67] :=dres = Dijkstra [gcur, 1]
Out[67] =
{{1, 13, 2, 9, 4, 4, 1, 13, 1, 8, 15, 9, 1, 3, 6, 10, 15},
{0, 1.11861, 1.2893, 0.958737, 1.17908, 1.34366,
0.391181, 1.08315, 0.811084, 1.27326, 1.6335,
1.38924, 0.692262, 1.6398, 1.34464, 1.48651, 1.41455}}
In [68]:= Column [
{TreePlot[gcur, Center, 1, VertexLabeling -> True,
DirectedEdges -> True,
PlotStyle -> {Arrowheads[{{.02, 0.5}}]}],
LayeredGraphPlot[gcur, VertexLabeling -> True,
DirectedEdges -> True] } , Spacer [4] ]Эта функция восстанавливает пути, найденные процедурой Dijkstra:
In [69] : = path[end_, start_, dij_] : =
Module[{ic, p, spt} , If[dij[[2, end]] == ∞ , {start},
spt = dij[[l]]; ic = end; p = {end} ;
While [spt[[ic]] \ne start, ic = spt[[ic]]; p= {ic} ≈ Join ≈ p] ;
{start} ≈ Join ≈ p]] ;
In [70] :=path[#, 1, dres] & /@ Drop [Range [17] , 1]
Out[70] =
{{1, 13, 2}, {1, 13, 2, 3}, {1, 9, 4}, {1, 9, 4, 5}, {1, 9, 4, 6}, {1, 7},
{1, 13, 8}, {1, 9}, {1, 13, 8, 10}, {1, 9, 4, 6, 15, 11}, {1, 9, 12}, {1, 13},
{1, 13, 2, 3, 14}, {1, 9, 4, 6, 15}, {1, 13, 8, 10, 16}, {1, 9, 4, 6, 15, 17}}Если забыть про ориентацию ребер, то кратчайшие пути могут измениться, так как возникают дополнительные возможности:
In [71]:=
DynamicModule [ {n = 11, gres = gcur} ,
(*gcur=SetEdgeWeights [ RandomGraph [ 11, . 2 , Type -> Directed] ] ; *)
Manipulate [If [dir, gres = gcur, gres = MakeUndirected [gcur] ] ;
shortPShowL [gcur, ShortestPath [gres, i, j] , i, j , dir] ,
{{i, 1, "Начальная вершина"}, Range[V[gcur]], ControlType -> PopupMenu},
{{j, 2, "Терминальная вершина"}, Range[V[gcur]],
ControlType -> PopupMenu} ,
{{dir, True, "Ориентируемость"}, {True, False}},
SaveDef initions -> True] ,
Initialization : -> (Needs["Combinatorica' "] ;
edgeW[g_, e_] : = GetEdgeWeights [g, {e}][[l]],
shortPShowL[g_, p_, ii_, jj_r test_] : =
Module [{edg, 11, ends, e = 0.1},
edg = Table [Take [p, {i, i + 1}], {i, 1, Length [p] - 1}] ; ends = {ii, Jj} ;
11 = edg ≈ Join ≈ (RotateLeft[#, 1] & /@edg) ;
If [Length [p] < 2,
Show[{Graphics[Text[Style["Путей НЕТ", Red, Bold, Large] , {0, 0}] ] ,
LayeredGraphPlot[g,
EdgeRenderingFunction ->
(If [test, {Black, Arrowheads[{{.02 , 0.5}}], Arrow[#1]},
{Black, Line[#l]}] &),
VertexRenderingFunction ->
({If[MemberQ[ends, #2] , Pink, White] , EdgeForm[Black] ,
Disk[#, .5] , Black, Text[#2, #1]} &) , ImageSize -> 600]
}],
LayeredGraphPlot [cr, EdgeRenderingFunction ->
(If[MemberQ[ll, #2], {Red}, {Orange, Opacity[0.5]}] ≈
Join ≈ If [test, {Arrowheads [{{ .02, 0.5}}], Arrow[#1]} ,
{Line [#1]}] &),
VertexRenderingFunction ->
({Which [MemberQ [ends, #2] , Pink, MemberQ[p, #2] , LightBlue,
True, White], EdgeForm[Black], Disk[#, .5], Black,
Text[#2, #1]} &) , ImageSize -> 600] ] ])]Если выделенной вершины нет, то проще воспользоваться процедурой ShortestPath. Для визуализации воспользуемся продвинутыми возможностями GraphPlot3D. Ребра изобразим в виде разноцветных цилиндров разной толщины. Толщина и цвет зависят от веса. Ребра кратчайшего пути выделены матовым красным. Номера концевых вершин пути - черные, промежуточных вершин - синие. Напомним, что, двигая мышкой при нажатой клавише Alt, можно приблизить/удалить объект, а при нажатой клавише Shift - сместить его в сторону:
In [72] :=
DynamicModule[{},
(*gcur=SetEdgeWeights[ RandomGraph[11, . 2,Type -> Directed]];*)
Manipulate[shortPathShow[gcur, ShortestPath[gcur, i, j], r] ,
{{i , 1} , Range[V[gcur]] , ControlType -> PopupMenu},
{{j 2}, Range[V[gcur]] , ControlType -> PopupMenu},
{{r, 0.1}, 0.01, 0.4}, SaveDefinitions -> True] ,
Initialization: -> (Needs [ "Combinatorica" ] ;
edgeWeight[g_, e_] : = GetEdgeWeights[g, {e}];
shortPathShow[g_ , p_ , r_ ] :=
Module[{edg, 11, ends, 6 = 0.1},
edg = Table [ Take [p, {i, i + 1}], {i, 1, Length[p] -1}] ;
ends = {pill, Pl-l]};
11 = edg≈ Join ≈ (RotateLef t [# , 1] & /@ edg) ;
If[Length[p] < 2,
Show[
{Graphics3D[Text[Style["Нет пути!", Red, Bold, Large],
{0, 0, 0}]] ,
GraphPlot3D[g,
EdgeRenderingFunction ->
({Hue[edgeWeight[g, #2]] ,
Cylinder [#1, r edgeWeight [g, #2]]} &) ,
VertexRenderingFunction ->
({Yellow, Sphere [#1, r + 0.03],
Text[Style[#2, Green, Bold, Large],
#1+ {e , e, e}]} &), ImageSize -> 500,
Viewpoint -> {3.25, 0.57, 3.25}]
}],
GraphPlot3D[g,
EdgeRenderingFunction ->
(If[MemberQ[ll, #2] , {Glow[Black] , Red},
{Lighter [Hue [edgeWeight [gr, #2]], .5]}] ≈ Join ≈
{Cylinder[#l, Max [r edgeWeight [g, #2], 0.01]]} &) ,
VertexRenderingFunction ->
({If [MemberQ[p, #2 , Red, Yellow] , Sphere [#1, r + 0.03] ,
Text[Style[#2, Which[MemberQ[ends, #2], Black,
MemberQ[p, #2] , Blue, True, Green], Bold, Large] ,
#1 + {e, e , e} ] } &) , Boxed -> False, ImageSize -> 500 ,
Viewpoint -> {3.25, 0.57, 3.25}]
]])]В следующем варианте картинка двумерная, веса ребер снова проиллюстрированы их толщиной. Зато хорошо видны стрелки:
In [73] : =
DynamicModule[{n = 11},
Manipulate[shortPShow[gcur, ShortestPath[gcur, i, j],
if jf r] , {{i, 1} , Range [V [gcur]] ,
ControlType -> PopupMenu} ,
{{j, 2} , Range[V[gcur]], ControlType -> PopupMenu},
{{r, 0.003}, 0.003, .01}, SaveDefinitions -> True],
Initialization : -> (Needs [ "Combinatorica' " ] ;
edgeW[g_, e_] : = GetEdgeWeights [g, {e}][[l]];
shortPShow [g_, p_, H_, jj_t *_] : =
Module[{edg, 11, ends, 6 = 0.1},
edg = Table [Takefp, {i, i + 1}], {i, 1, Length [p] - 1}] ;
ends = {ii, jj) ;
11 = edg ≈ Join ≈ (RotateLef t [#, 1] & /@ edg) ;
If[Length[p] < 2,
Show[
{Graphics[Text[Style["Путей НЕТ", Red, Bold, Large],
{0, 0}]],
GraphPlot[g,
EdgeRenderingFunction ->
({Black, Arrowheads[{{0.02, 0.5}}] ,
Arrow[#l]} &),
VertexRenderingFunction ->
({If[MemberQfends, #2] , Pink, White],
EdgeForm[Black] , Disk[#, .1] , Black,
Text [#2, #l } &) , ImageSize -> 500]
}],
GraphPlot[g,
EdgeRenderingFunction ->
(If[MemberQ[ll, #2], {Blue},
{Orange, Opacity[0.5]}] ≈ Join ≈
{Thickness [r edgeW[g, #2]],
Arrowheads [{{3 r , 0.5}}] , Arrow [#l, .1]} &) ,
VertexRenderingFunction ->
( {Which [MemberQ [ends, #2] , Pink, MemberQ[p, #2],
LightBlue, True, White], EdgeForm[Black],
Opacity[0.7], Disk[#, .1] , Opacity[1] ,
Black, Text[#2, #l] } &) , ImageSize -> 500]
]])]