Графы в компьютерной геометрии
Графы в пакете Mathematica
В пакете Mathematica предусмотрено две группы средств для работы с графами. Одна предназначена для создания, хранения и преобразования информации в виде графов. Другая, с которой мы познакомились в предыдущем разделе, - для визуализации уже имеющихся графов.
Графы: способы задания
Описываемые здесь процедуры являются частью пакета Combinatorica, поэтому перед началом работы с ними следует выполнить команду, загружающую этот пакет:
In[14] := Needs [ "Combinatorica' " ]
Граф в пакете Combinatorica задается командой Graph[<список ребер>,<список вершин>,<список опций графа в целом>] , где каждое ребро (т. е. элемент списка ребер) имеет вид {{<номер вершины>, <номер вершины >},<опции ребра>} , каждая вершина (т. е. элемент списка вершин) имеет вид {{координаты вершины на плоскости\},<опции>} , и, наконец, в списке опций стоят общие команды для всех вершин, всех ребер и графа в целом. Обратим внимание на двойные фигурные скобки, которые объясняются возможным наличием опций.
В пакете Combinatorica также имеются встроенные функции для визуализации графов, такие как ShowGraph[< граф >] или ShowGraphArray.
In[15]:=ShowGraph[Graph[{{{l, 2}}, {{2, 3},
EdgeColor -> Red}, {{3, 1}}}, {{{-1, 0}},
{{1, 1}, VertexColor -> Blue,
VertexStyle -> Disk[Large]}, {{1, 0}}}]]Более сложный пример. В нем положение вершин задано случайно, а количество и соседство можно регулировать. Кроме того, справа тот же граф перерисован с установкой общих опций, регулирующих вид вершин и ребер. Заметим, что внешние опции, если установлены, перекрывают соответствующие опции, установленные для конкретных вершин (ребер):
In[16] : =
Manipulate [Module [{w, ее, gg} ,
If [k > n- 1, k = n- 1] ;
If [n ≠ Length [w] ,
vv = Map[{#, VertexNumber -> True} &, Table [ {Random [] , Random []} , {n}]]];
ее =
Table [{{i, Mod[i + k, n] + 1} , If [Mod [i, 2] = =0, EdgeColor -> Red,
EdgeColor -> Green] } , {i, 1, n} ]; g = Graph [ее, vv] ;
gg = Graph [ее, vv, {EdgeStyle -> edgSt, VertexStyle -> vrSt}] ;
GraphicsRow[{ShowGraph[g], ShowGraph[gg]}]], {{n, 4}, 2, 27, 1},
{{k, 1}, 0, n-1, 1}, {{edgSt, {Green, Red}, "Вид ребра"},
{{Blue} -> "Синий", {Dashed} -> "Пунктир", {Blue, Dashed} -> "Синий-Пунктир" } } ,
{{vrSt, {Disk[Normal]}, "Размер вершины"},
{{Disk[Normal] } -> "Нормальный" , {Disk[Small] } -> "Мелкий" ,
{Disk[Medium] } -> "Средний", {Disk[Large] } -* "Крупный"}},
Initialization: -> (Needs ["Combinatorica" "] )]Граф, заданный в пакете Combinatorica, можно визуализировать с помощью GraphPlot или GraphPlot3D. Картинка будет куда нагляднее, однако часть информации, такая как цвета ребер и пр., при этом теряется:
In[17] :=Dynamic[GraphPlot3D[g] ]
Отметим, что описанные способы задания графов громоздки и не всегда удобны. Имеется ряд возможностей конструировать графы из более привычных наборов данных, служащих для описания графов. Так можно породить неориентированный граф из списка неупорядоченных пар вершин FromUnorderedPairs[<список>], и ориентированный граф - из списка упорядоченных пар вершин FromOrderedPairs[<список>]. Также граф можно породить из матрицы вершинной смежности FromAdjacencyMatrix[m] и из списков вершинной смежности FromAdjacencyLists[l] :
In [18]:= listOfUnPairs = {{1, 2}, {1, 3}, {1, 4},
{1, 5}, {1, 6}, {2, 3}, {3, 4}, {4, 5},
{5, 6}, {6, 2}};
vc= {{0, 0}} ≈ Join ≈
Map[{Cos[ ((2 π)/5) #] , Sin[((2 π)/5 #]} &, Range [5]] ;
g1= FromUnorderedPairs[listOfUnPairs] ;
g11 = FromUnorderedPairs[listOfUnPairs, vc] ;
ShowGraphArray[{gl, gl 1} ]Отметим, что для такого задания графа координаты вершин, вообще говоря, не нужны. Mathematica сама выберет в качестве них по умолчанию равномерный набор точек на окружности. Последнее, впрочем, не всегда хорошо отражает суть дела. Если нам не нравится выбор Mathematica, то имеется возможность задать точки самим, для чего используется второй необязательный аргумент.
Как мы уже говорили, другой способ получения наглядной картинки - воспользоваться GraphPlot. Использование этой команды, однако, таит в себе некоторые неожиданности. Если, например, включить опции, показывающие направления ребер и их кратность, то мы увидим, что наш неориентированный простой граф воспринимается на самом деле как ориентированный:
In [23] :=GraphicsRow[ {GraphPlot [g1] ,
GraphPlot[g1, DirectedEdges -> True,
MultiedgeStyle -> True] } ]Из тех же данных можно породить ориентированный граф командой FromOrderedPairs[<список>]:
In[24]=g2 = FromOrderedPairs [listOfUnPairs] ;
g21 = FromOrderedPairs[listOfUnPairs, vc] ;
ShowGraphArray[{g2, g21} ]Теперь и GraphPlot даст нам тот ориентированный граф, который мы задавали на самом деле:
In [27] := GraphPlot [g2 , DirectedEdges -> True,
MultiedgeStyle -> True]При помощи команды FromAdjacencyMatrix[m] можно породить как неориентированный граф, так и ориентированный (при этом обязательно выставить опцию Type \to . Directed, иначе получится неориентированный граф, заданный верхним треугольником матрицы смежности). Кроме того, имеется возможность задать граф с кратными ребрами (в этом случае элементы матрицы интерпретируются как кратность ребер):
![In[28]:=m1=\begin{pmatrix}
0&1&1&1&1&1\\
1&0&1&0&0&1\\
1&1&0&1&0&0\\
1&0&1&0&1&0\\
1&0&0&1&0&1\\
1&1&0&0&1&0
\end{pmatrix}; m2=
\begin{pmatrix}
0&1&1&1&1&1\\
0&0&1&0&0&0\\
0&0&0&1&0&0\\
0&0&0&0&1&0\\
0&0&0&0&0&1\\
0&1&0&0&0&0
\end{pmatrix}; \\m3=
\begin{pmatrix}
0&3&1&4&1&1\\
3&0&1&0&0&1\\
1&1&0&6&0&0\\
4&0&6&0&15&0\\
1&0&0&15&0&1\\
1&1&0&0&1&0
\end{pmatrix};](/sites/default/files/tex_cache/37e5420a16f69b3169cf9e188701dcd4.png)
g3 = FromAdjacencyMatrix [m1] ; g31 = FromAdjacencyMatrix [ml, vc] ;
g32 = FromAdjacencyMatrix [m2, vc, Type -> Directed] ;
g33 = FromAdjacencyMatrix [m3 , vc] ;
ShowGraphArray [ {g3 , g31, g32 , gЗЗ}]In [32] :=
GraphicsRow[ GraphPlot[
#, DirectedEdges -> True, MultiedgeStyle -> True] &/@
{gЗ, g32, gЗЗ}]Наконец, можно задать взвешенный граф, т. е. приписать ребрам графа некоторые числа, называемые весами. Установка опции EdgeWeight порождает взвешенный граф, в чем можно убедиться, выведя список ребер командой Edges. Теперь элементы матрицы интерпретируются как веса. Для отсутствующих ребер следует в этом случае ставить  (а не нуль).
(а не нуль).
![In[33]:=m4=\begin{pmatrix}
\infty&3&1&4&1&1\\
3&\infty&1&\infty &\infty &1\\
1&1&\infty&6&\infty&\infty\\
4&\infty&6&\infty&15&\infty\\
1&\infty&\infty&15&\infty&1\\
1&1&\infty&\infty&1&\infty
\end{pmatrix};](/sites/default/files/tex_cache/02fe107288e71ac0bee87b6324325a17.png)
g34 = FromAdjacencyMatrix[m4, vc, EdgeWeight] ;
el = Edges[g34, EdgeWeight]
Out[35] =
{{{1, 2}, 3}, {{1, 3}, 1}, {{1, 4}, 4}, {{1, 5}, 1}, {{1, 6}, 1},
{{2, 3}, 1}, {{2, 6}, 1}, {{3, 4}, 6}, {{4, 5}, 15}, {{5, 6}, 1}}Чтобы визуализировать веса ребер взвешенного графа, можно установить значения меток ребер равными соответствующим весам (это делается с помощью команды SetEdgeLabels[<граф>,<список меток>]) и выставить опцию {EdgeLabel \to True}. Обратите внимание: команда SetEdgeLabels не меняет метки исходного графа, а создает новый граф:
In [36] :=g35 = SetEdgeLabels [g34, #[[2]] & /@ el] ;
ShowGraphArray[{g35, д34}, {EdgeLabel -> True}]Кроме того, можно снова воспользоваться GraphPlot, применяя функцию EdgeRenderingFunction для визуализации значений весов ребер. Отметим, что GraphPlot воспринимает графы старого формата так, что каждое ребро учетверяется: две копии ориентированы в одну сторону, а две другие - в другую. Ниже предлагается реализация функции прорисовки ребра, основанная на том, что функция GetEdgeWeights не различает направления ребер:
In[38] :=
GraphPlot [g34 , EdgeRenderingFunction ->
( {Line [#1] , Inset [Style [" " <> ToString @@ GetEdgeWeights [g34 , {#2}] <>" ",
Red, Large] , Mean[#1] , Automatic, Automatic, #1[[1]] - #2[[2]],
Background -> White] } &) ]Наконец, для задания графов можно воспользоваться списками смежности и командой FromAdjacencyLists. Отметим, что в этих списках также допускается указывать веса ребер. Списки смежности устроены следующим образом: на i -м месте стоит список номеров вершин, смежных с i -й вершиной. Если надо указать веса ребер, то в i -м списке вместо номера j ставится пара вида  , где
, где 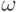 - вес ребра ij:
- вес ребра ij:
In [39] :=
(*Обычные списки смежности *)
11= {{2, 3, 4, 5, 6}, {1, 3, 6}, {1, 2, 4}, {1, 3, 5} , {1, 4, 6}, {1, 2, 5}};
vc = {{0, 0}} ≈ Join ≈ Map [{cos[((2 π)/5) #] , Sin[((2 π)/5)#]} &, Range [5] ] ;
g4 = FromAdjacencyLists [11] ; g41 = FromAdjacencyLists [11, vc] ;
(*Списки смежности с весами *)
lw= {{{2, 1}, {3, 3}, {4, 2}, {5, 1}, {6, 2}}, {{1, 1}, {3, 2}, {6, 3}},
{{1, 3}, {2, 2}, {4, 5}}, {{1, 2}, {3, 5}, {5, 1}}, {{1, 1}, {4, 1}, {6, 6}},
{{1, 2}, {2, 3}, {5, 6}}};
g42 = FromAdjacencyLists[lw, EdgeWeight];
(*Устанавливаем метки ребер равными их весам *)
g43=SetEdgeLabels[g42, #[[2]] & /@ Edges[g42, EdgeWeight]];
ShowGraphArray [ {g4 , g41, g43} , VertexNumber -> True , EdgeLabelColor ->Red]Если граф уже есть, то можно получить из него набор соответствующих (упорядоченных) пар, матрицу смежности, списки смежности с помощью обратных команд ToUnorderedPairs, ToOrderedPairs, ToAdjacencyMatrix и ToAdjacencyLists, соответственно. При этом надо внимательно следить за опциями. Например, отсутствие опции EdgeWeight приводит к потере информации о весах ребер:
In [46] : =
11= {{{2, 0.1}, {2, π //N}, {3, .13}},
{{2, √3 // N}, {3, Log[2] //N}}, {}};
(*ll={{{2,10},{2, π //N},{3,.13}},{{2, √3 //N},{3,Log[2]//N}},
{}};*)
gr = FromAdjacencyLists[11, EdgeWeight, Type -> Directed];
Row[{ShowGraph[gr, EdgeLabel -> GetEdgeWeights[gr],
EdgeLabelColor -> Red,
EdgeLabelPosition -> {{ .0, .05}, {.1, -.05}, {.05, .05}, \
{.05, .05}, {.05, .05}}],
ToAdjacencyMatrix[gr, EdgeWeight] // MatrixForm,
ToAdjacencyMatrix[gr] //MatrixForm}, Spacer[64]]Обратите внимание, что при переходе к матрице смежности веса кратных ребер теряются, несмотря на опции (из них берется максимальный). Ориентируемость - сохраняется. Отметим также, что визуализировать веса кратных ребер с помощью меток не тривиально, так как, во-первых, некорректно работает функция SetEdgeLabels и положения меток кратных ребер по умолчанию совпадают:
In [49]:=11= {{{2, .1}, {2, π //N}, {3, .13}},
{{2, √3//N}, {3, Log[2] //N}}, {}};
gr = FromAdjacencyLists[11, EdgeWeight, Type -> Directed];
wgh = GetEdgeWeights[gr]
grr = SetEdgeLabels[gr, wgh] ;
Edges[grr. All]
Out[51] = {0.l, 3.14159, 0.13, 1.73205, 0.693147}
Out[53] = {{{1, 2}, EdgeWeight -> 0 .1, EdgeLabel -> 0.1},
{{1, 2}, EdgeWeight -> 3.14159, EdgeLabel -> 0 .1},
{{1, 3}, EdgeWeight -> 0.13, EdgeLabel -> 0 .13},
{{2, 2}, EdgeWeight -> 1.73205, EdgeLabel -> 1.73205},
{{2, 3}, EdgeWeight -> 0. 693147, EdgeLabel -> 0 . 693147 }}Во-вторых, некорректно работает функция SetEdgeWeights:
In [54]:=ll= {{2, 2, 3}, {2, 3}, {}} ;
gr = FromAdjacencyLists[11, Type -> Directed];
grr = SetEdgeWeights[gr, { . 1, . 2 , . 3 , . 4 , .5}] ;
Edges[grr, All]
Out[57] = {{{1, 2}, EdgeWeight -> 0.1},
{{1, 2}, EdgeWeight -> 0.1}, {{1, 3}, EdgeWeight -> 0 . 3},
{{2, 2}, EdgeWeight -> 0 . 4 }, {{2, 3}, EdgeWeight -> 0.5}}












