Кривые и поверхности в компьютерной геометрии, I
Деление рациональной кривой Безье
Для заданного  из интервала
из интервала 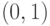 требуется построить два новых набора опорных точек и весов
требуется построить два новых набора опорных точек и весов 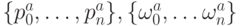 и
и  так, чтобы кривые Безье, построенные по этих новым наборам, совпали бы (как геометрическое место точек) соответственно с двумя дугами исходной кривой Безье, на которые она разбивается точкой
так, чтобы кривые Безье, построенные по этих новым наборам, совпали бы (как геометрическое место точек) соответственно с двумя дугами исходной кривой Безье, на которые она разбивается точкой 
Данная задача имеет важное значение в теории кривых Безье. Необходимость деления кривых Безье возникает в тех случаях, когда требуется изменить какую-то часть кривой, оставляя некоторую другую ее часть неизменной. Поскольку смещение любой опорной точки кривой Безье меняет всю ее в целом, возникает необходимость разбивать кривую Безье на несколько частей. Это дает возможность менять только одну из получившихся частей исходной кривой Безье (ставших уже самостоятельными кривыми Безье), не трогая остальные части исходной кривой.
Деление рациональной кривой Безье сводится к делению обычной кривой Безье, которая порождает данную рациональную кривую.
Рассмотрим рациональную кривую Безье, построенную по опорным точкам  с весами
с весами  Обозначим ее через
Обозначим ее через ![r_0(t; n), t \in [0,1] .](/sites/default/files/tex_cache/153c19d649cd19292320f41fae7717b6.png) Как мы знаем, эта кривая порождается обычной кривой Безье, построенной по вспомогательным опорным точкам
Как мы знаем, эта кривая порождается обычной кривой Безье, построенной по вспомогательным опорным точкам  которые зависят от выбора начала координат. При этом начало координат необходимо выбирать так, чтобы оно не совпадало ни с одной из опорных точек
которые зависят от выбора начала координат. При этом начало координат необходимо выбирать так, чтобы оно не совпадало ни с одной из опорных точек  Обозначим построенную таким образом вспомогательную обычную кривую Безье через
Обозначим построенную таким образом вспомогательную обычную кривую Безье через ![\hat r_0(t;n), t \in [0,1] .](/sites/default/files/tex_cache/3e3e383f699cbf54901479c26afcb1cb.png) Разделим вспомогательную кривую
Разделим вспомогательную кривую  в точке
в точке  в отношении
в отношении  как это делалось выше. Таким образом, возникает три вспомогательные (обычные) кривые Безье:
как это делалось выше. Таким образом, возникает три вспомогательные (обычные) кривые Безье:
 - это кривая Безье, построенная по опорным точкам
- это кривая Безье, построенная по опорным точкам ![\hat p_0, \dots ,\hat p_n , t \in [0,1],](/sites/default/files/tex_cache/f214e528ff0bdf46d38d2998f89338aa.png)
 - это кривая Безье, построенная по опорным точкам
- это кривая Безье, построенная по опорным точкам ![\hat p_0^a, \dots ,\hat p_n^a, s \in [0,1],](/sites/default/files/tex_cache/23751d4187dcfe9222adfb504eb8bc6a.png)
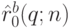 - это кривая Безье, построенная по опорным точкам p
- это кривая Безье, построенная по опорным точкам p ![\hat p_0^b, \dots , \hat p_n^b, q \in [0,1].](/sites/default/files/tex_cache/832dbfd83745807b154d364d9ea4fd6b.png) Здесь
Здесь
 |
( 5.28) |
Кривые Безье  и
и  порождают две рациональные кривые Безье
порождают две рациональные кривые Безье  и
и 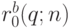 по следующему правилу:
по следующему правилу:
 - рациональная кривая Безье, построенная по опорным точкам
- рациональная кривая Безье, построенная по опорным точкам  с весами
с весами 
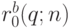 - рациональная кривая Безье, построенная по опорным точкам
- рациональная кривая Безье, построенная по опорным точкам  с весами
с весами  где
где
 |
( 5.29) |
 |
( 5.30) |
Из формул (5.28), (5.29) и (5.30) следует, что
 |
( 5.31) |
Равенства (5.31) означают, что кривые Безье  и
и  соответствуют рациональным кривым Безье
соответствуют рациональным кривым Безье  и
и 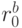 с весами
с весами  и
и 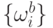 соответственно.
соответственно.
Лемма 5.3. Кривые  и
и  делят кривую
делят кривую  в точке
в точке  в отношении
в отношении 
Доказательство см. в [1].
Увеличение числа опорных точек рациональной кривой Безье
Операция увеличения числа опорных точек рациональной кривой Безье сводится к уже известной нам операции увеличения числа опорных точек обычной кривой Безье в пространстве  и применению отображения
и применению отображения  Более подробно, алгоритм состоит в следующем.
Более подробно, алгоритм состоит в следующем.
- По данной рациональной кривой Безье
 определяемой опорными точками
определяемой опорными точками  и весами
и весами 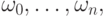 строим обычную кривую Безье
строим обычную кривую Безье  в пространстве
в пространстве  определяемую опорными точками
определяемую опорными точками 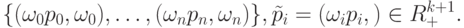 Тогда
Тогда 
-
Увеличиваем число опорных точек обычной кривой Безье
 на единицу способом, описанным в разделе 3.6. А именно, строим новые опорные точки
на единицу способом, описанным в разделе 3.6. А именно, строим новые опорные точки 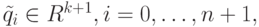 по формуле
по формуле
Точки
 и
и 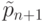 можно определить произвольно, т. к. они входят в правую часть последней формулы с нулевыми коэффициентами.
можно определить произвольно, т. к. они входят в правую часть последней формулы с нулевыми коэффициентами. -
Применяем к новым опорным точкам
 преобразование
преобразование  Поскольку кривая Безье
Поскольку кривая Безье  определяемая опорными точками
определяемая опорными точками  - это та же самая кривая, что и
- это та же самая кривая, что и  то
то  Но одновременно по определению рациональной кривой Безье имеем:
Но одновременно по определению рациональной кривой Безье имеем:  где
где  - рациональная кривая Безье, определяемая опорными точками и весами
- рациональная кривая Безье, определяемая опорными точками и весами  где
где  -е компоненты точек
-е компоненты точек  в
в 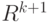
Окончательные формулы имеют вид

где
 - исходные опорные точки и веса данной рациональной кривой Безье i а
- исходные опорные точки и веса данной рациональной кривой Безье i а 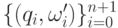 - новые опорные точки и веса той же кривой, но - с увеличенным на единицу количеством опорных точек (и, соответственно, с большим на единицу количеством весов).
- новые опорные точки и веса той же кривой, но - с увеличенным на единицу количеством опорных точек (и, соответственно, с большим на единицу количеством весов).
