НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 5: Кривые и поверхности в компьютерной геометрии, I

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1030 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00

ISBN: 978-5-9556-0117-5

Темы: Математика, САПР

Специальности: Математик

Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Составной сплайн Эрмита

Составной сплайн Эрмита предназначен для построения кривой заданной степени гладкости, проходящей через заданную последовательность опорных точек. Он получается путем соединения соседних опорных точек сплайнами Эрмита одного и того же порядка. При этом значения производных радиус-вектора в опорных точках (требуемые для построения составляющих сплайнов Эрмита) необходимо как-то доопределять. Это можно сделать по-разному, исходя из различных соображений. Простые способы доопределения производных приводят к простым вычислениям, однако при неравномерном расположении опорных точек такой сплайн может образовывать необоснованные петли и изгибы. Более сложные способы доопределения производных (псевдоупругие сплайны Эрмита, например) дают хорошие результаты, но приводят к большим вычислениям.

Пример 5.2.3. Составной сплайн Эрмита порядка 3 ( m = 1 ). Для построения такого сплайна необходимо предварительно доопределить первые производные радиус-вектора в опорных точках $p_0, \dots ,p_n.$ Для промежуточных и крайних опорных точек способ доопределения различен.

Промежуточные опорные точки. В промежуточных опорных точках можно, например, положить производные 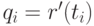равными

$q_i=\frac{p_{i+1}-p_{i-1}}{t_{i+1}-t_{i-1}}, 1 \le i \le n-1$
т. е. рассмотреть аппроксимацию производных.

Однако при неравномерном расположении опорных точек такой способ доопределения производных может привести к появлению необоснованных петель. Поэтому обычно пользуются другими схемами доопределения Например, можно положить

$q_i=s_{i+1}\frac{p_1-p_{i-1}}{s_i+s_{i+1}}+s_i \frac{p_{i+1}-p_i}{s_i+s_{i+1}}$
или

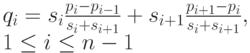
$q_i=s_i \frac{p_i-p_{i-1}}{s_i+s_{i+1}}+s_{i+1} \frac{p_{i+1}-p_i}{s_i+s_{i+1}},\\ 1 \le i \le n-1$
где $s_i = ||p_i - p_{i-1}||$ - расстояние между оседними опорными точками.
Крайние опорные точки. В двух крайних опорных точках если в них не требуется гладко стыковать сплайн с другими, уже заданными кривыми, обычно пользуются условием равенства нулю третьих производных радиус-вектора на концах (условие свободных концов кривой): $r^{(3)}(t_0) = 0, r^{(3)}(t_n) = 0.$ Можно показать, что соответствующие значения первых производных на концах составного сплайна Эрмита третьего порядка даются формулами

$q_0 = 2(p_1 - p_0) - q_1, \\ q_n = 2(p_n - p_{n-1}) - q_{n-1}.$

Задача 5.2.3. С помощью программы, рисующей составной сплайн Эрмита третьего порядка, изучить поведение этого сплайна в зависимости от расположения опорных точек, конфигурации узлов и способа доопределения производных в промежуточных точках (поменяйте в программе способ доопределения производных в промежуточных точках на другой и сравните результат).

Пример 5.2.4. Составной сплайн Эрмита третьего порядка с шестью управляемыми мышью опорными точками:

In[5]:=
       DynamicModule Г {pts , ptsO, n,  t, tt, i,  j, S, gO, gl, h0, hi, w, q, r} ,  
        pts0 = {{6.0,  -5.0},   {0.0,  0.0},   {4.8, 5.2},   {0.3,  7.5},   {6.8,  12.2},   {-2.3,  0.0}}; 
           tt= {1.0, 2.0,  3.0,  6.0,  7.0,  8.0}; 
           n = Length[ptsO] - 1; 
           Manipulate [ 
              S = Table [{r[i,  t, pts] ,  tt [ [i] ]  <=. t <== tt [ [i + 1] ] } ,   {i,  1, n} ] ; 
             Show[{ParametricPlot[
                 Piecewise[S] ,   {t,  tt[ [1] ] ,  tt [ [-1] ] } , PlotRange -> {{-10, 20},   {-10, 20}}
               ],
              Graphics [{Red, Text[ToString[* - 1] , pts [ [*] ] +{1.2, 0}]  &/@Range [n + 1] , 
                       Text["Составной сплайн Эрмита 3 порядка",  {7, -9}]}]}], 
               {{pts, ptsO} , Locator}] ,  Initialization: -> (
                  g0 [x_]   : = 2 x³ - 3 x² + 1; gl [x_] : = x³ - 2 x² + x; h0 [x_]: = 3 x² - 2 x³ ; 
                  h1 [x_]   : = x³ - x² ;
                  w[i_,  t_]   :=  (t-tt[[i]]) / (tt[[i + l]] -tt[[i]]); 
                  q[i_, pts_] : = 
                     If[i==l, 2 (pts [[2]] -pts[[l]]) - (pts[[3]] -pts[[l]]) / (tt[[3]] -tt[[l]]), 
                        If[i==n + 1, 2 (pts [ [n + 1] ] - pts [ [n] ] ) -
                             (pts[[n + 1]] -pts[[n-l]]) / (tt[[n + l]] -tt[[n-l]]) , 
                           (pts[ [i + 1]] -pts[[i-l]]) / (tt[[i + l]] -tt[[i-l]])]]; 
                     r [i_,   t_, pts_]   : = gO [w[i,   t] ] * pts[ [i] ] + gl [w[i,   t] ] *q[i, pts] + 
                        h0[w[i,  t] ] *pts[ [i + 1] ] +hl[w[i,  t] ] *q[i + 1, pts] ) ]

Псевдоупругие сплайны Эрмита

При построении составного сплайна Эрмита третьего порядка неизвестные производные 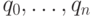$q_0, \dots ,q_n$ в точках $p_0, \dots ,p_n$ могут быть определены также из следующих соображений.

Представим себе, что через точки $p0, \dots ,p_n$ должна пройти упругая нить, которая стремится занять положение, соответствующее минимуму запасенной энергии ее внутренних сил упругости. Эта энергия, как известно из физики, выражается интегралом от квадрата кривизны k(s) кривой, по которой пролегает нить:

$E=\frac12 \int_{t_0}^{t_n}c(s)k^2(s)ds,$

( 5.3)

где s - натуральный параметр на кривой, а c(s) - коэффициент упругости нити. Мы будем считать, что c(s) = c = const.

Предположим, что искомый сплайн задается графиком функции y = y(x). Поскольку минимизация энергии упругих сил (5.3) является, вообще говоря, достаточно трудоемкой вычислительной задачей, мы заменим ее на более простую, но достаточную для наших целей задачу. А именно, заменим энергию E, задаваемую формулой (5.3), на псевдоупругую энергию, заменив кривизну k на модуль второй производной $\left | \frac{d^2y}{dx^2} \right |.$ Это приводит к задаче минимизации интеграла

$E=\frac12 \sum_{i=0}^{n-1} \int_{x_i}^{x_{i+1}}(y''(x))^2dx$ ( 5.4)

за счет выбора величин 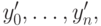$y_0', \dots, y_n',$ где Условие стационарной точки целевой функции (5.4), получаемое приравниванием к нулю ее частных производных, имеет вид

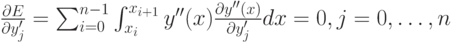
$\frac{\partial E}{\partial y_j'}=\sum_{i=0}^{n-1} \int_{x_i}^{x_{i+1}}y''(x) \frac{\partial y''(x)}{\partial y_j'}dx=0, j=0, \dots, n$ ( 5.5)

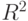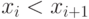Пусть точки $p_0, \dots , p_n$ на имеют координаты $(x_0, y_0), \dots , (x_n, y_n)$ соответственно. Будем считать, что $x_i < x_{i+1}$ для любого $i, 0 \le i \le n - 1.$ Введем обозначения: $\Delta i = x_{i+1} -x_i.$ Тогда местный параметр на участке $(x_i,x_{i+1})$ будет равен $w = \frac{x- x_i}{\Delta _i}.$ На отрезке $[x_i,x_{i +1}]$ обозначим через $y_{i, i+1}(x).$

Согласно (5.1), на участке $(x_i, x_{i+1}), i = 0, \dots , n - 1,$ зависимость

$\tilde y_{i,i+1}(w)=y_{i,i+1}(x(w))$
имеет вид

$\tilde y_{i, i+1}(w)=y_ig_0(w)+y_{i+1}h_0(w)+y_i' \Delta_ig_1(w)+y_{i+1}' \Delta_ih_1(w)$ ( 5.6)

поскольку $y_i'=\frac{dy_{i,j+1}}{dx} \left |_{x=x_i}= \frac{1}{\Delta_i} \frac{d \tilde y_{i, j+1}}{dw} \left |_{x=x_i}$ и $y_{i+1}'=\frac{dy_{i,j+1}}{dx} \left |_{x=x_{i+1}}=\frac{1}{\Delta_i} \frac{d \tilde y_{i,j+1}}{dw} \left |_{w=1}.$

Подставляя (5.6) в (5.5), интегрируя по частям, пользуясь явным видом функций из (5.2), а также тем, что $\frac{d^4y}{dx^4},$ приходим к следующей системе уравнений:

$\begin{cases} y_{i-1,i}''(x_i)=y_{i,i+1}''(x_i), i=1, \dots, n-1\\ y_{0,1}''(x_0)=y_{n-1,n}''(x_n)=0 \end{cases}$ ( 5.7)

которая обозначает, что вторые производные а следовательно, и кривизна кривой, должны быть непрерывны в точках стыковки $p_1, \dots ,p_{n-1},$ а на концах ? обращается в нуль.

Подставим теперь (5.6) в (5.7) и снова воспользуемся явным видом функций из (5.2). Используя равенства $y_{i,j+1}''(x_i)=\frac{1}{\Delta_i^2} \frac{d \tilde y_{i,j+1}}{dw} \left |_{w=0}$ и $y_{i,j+1}''(x_{i+1})=\frac{1}{\Delta_i^2} \frac{d \tilde y_{i,j+1}}{dw} \left |_{w=1}$ получим систему уравнений на c ленточной 3-шаговой матрицей:

$\begin{cases} y_{i-1}' \frac{1}{\Delta_{i-1}}+2y_i' \left ( \frac{1}{\Delta_{i-1}} + \frac {1}{\Delta_i} \right )+y_{i+1}'\frac{1}{\Delta_i}=3 \frac{y_i-y_{i-1}}{\Delta_{i-1}^2}+3 \frac{y_{i+1}-y_i}{\Delta_i^2},\\ 1 \le i \le n-1,\\ 2y_0' \Delta_0 + y_i' \Delta_0=3(y_1-y_0) (\mbox{граничное условие в точке} p_0\\ y_{n-1}' \Delta_{n-1}+2y_n' \Delta_{n-1}=3(y_n-y_{n-1})(\mbox{ граничное условие в} p_n) \end{cases}$
Это - система из ( n + 1 )-го уравнения с ( n + 1 ) неизвестным $y_0', \dots, y_n'.$ Поскольку матрица системы имеет ленточный вид, то она допускает численное решение за линейное по n время.
Теперь рассмотрим более общий случай параметрически заданного сплайна r = r(t) (т. е. не обязательно в виде графика функции y = y( x) ).

На участке между точками 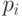p_i и $p_{i+1}$ обозначим искомый сплайн Эрмита порядка 3 через $r_i (w) (0 \le i \le n - 1) ,$ где $0 \le w \le 1$ - местный параметр. Имеем, согласно (5.1),

$r_i(w)=p_ig_0(w)+p_{i+1}h_0(w)+\dot r_i(0)g_1(w)+\dot r_i(1)h_1(w),\\ i=0, \dots, n-1$

( 5.8)

К этому надо добавить условия непрерывности первых производных в точках стыковки:

$\dot r_{i-1}(1)=k_i \dot r_i(0), i=1, \dots, n-1$

( 5.9)

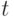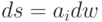где $k_i =\frac{t_i-t_{i-1}}{t_{i+1}-t_i}.$ Будем считать, что $\frac{|t_i-t_{i-1}|}{|t_{i+1}-t_i|}=\frac{|p_i-p_{i-1}|}{|p_{i+1}-p_i|}$ т. е. параметр пропорционален натуральному. Тогда и местный параметр будет также пропорционален натуральному. Обозначим $a_i = p_{i+1} - p_i, |a_i| = a_i.$ Из пропорциональности параметра натуральному следует, что ds = a_idw на участке $(t_i,t_{i+1}).$ Следовательно, кривизна пропорциональна $\frac{\ddot r_i}{a_i^2},$ а потому псевдоупругая энергия сплайна Эрмита может быть определена как

$E=\sum_{i=0}^{n-1} \frac{1}{a_i^3}\int_0^1(\ddot r_i(w))^2dw)$

( 5.10)

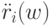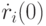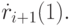При этом, согласно (5.8) и (5.9), $\ddot r_i(w)$ выражается через $\dot r_i(0)$ и $\dot r_{i+1}(1) .$ Условие стационарности (необходимое условие экстремума функции (5.10)) имеет вид

$\frac{\partial E}{\partial \dot r_i(0)}=0, i=0, \dots, n-1,\\ \frac{\partial E}{\partial \dot r_{n-1}(1)}=0$

( 5.11)

Подставляя (5.8) и (5.9) в (5.11), приведем (5.11) к виду

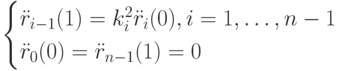
$\begin{cases} \ddot r_{i-1}(1)=k_i^2 \ddot r_i(0), i=1, \dots, n-1\\ \ddot r_0(0)= \ddot r_{n-1}(1)=0 \end{cases}$

где 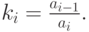$k_i=\frac{a_{i-1}}{a_i}.$ Подставим сюда (5.8). Получим после алгебраических преобразований следующее выражение:

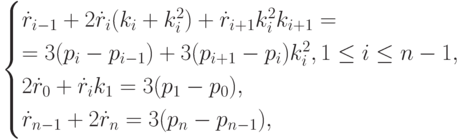
$\begin{cases} \dot r_{i-1}+2 \dot r_i(k_i+k_i^2)+\dot r_{i+1}k_i^2k_{i+1}=\\ =3(p_i-p_{i-1})+3(p_{i+1}-p_i)k_i^2, 1 \le i \le n-1,\\ 2 \dot r_0+\dot r_ik_1=3(p_1-p_0),\\ \dot r_{n-1}+2 \dot r_n=3(p_n-p_{n-1}), \end{cases}$

где $\dot r_i= \dot r_i(0), i=1, \dots, n-1, \dot r_n=\dot r_{n-1}(1).$ Эта система состоит из (n + 1) уравнений c (n+ 1) неизвестными $\dot r_0, \dots , \dot r_n.$ Как и выше, матрица системы является ленточной, т. е. ненулевые элементы в ней расположены лишь в узкой окрестности главной диагонали. Такие системы уравнений допускают численное решение за линейное время с помощью хорошо разработанных алгоритмов.

Задача 5.2.4. Написать программу построения псевдоупругого сплайна Эрмита на плоскости, имеющего вид графика функции и проходящего через заданную последовательность опорных точек с возрастающими абсциссами. Сравнить псевдоупругий сплайн Эрмита и составной сплайн Эрмита третьего порядка, проходящие через одни и те же опорные точки, путем изображения обоих сплайнов на одном графике.

Дальше >>

Авторизоваться

Практикум по компьютерной геометрии

Кривые и поверхности в компьютерной геометрии, I

Составной сплайн Эрмита

Псевдоупругие сплайны Эрмита

Вопросы и ответы