Элементы управления и динамика

Оператор Dynamic[]

Обычные вводы-выводы в Mathematica статичные. Вывод результата уже вычисленного выражения не меняется при дальнейшем изменении переменных, входящих в выражение. Последнее полезно для наблюдения за историей вычислений.

In[14]:=х = 3; 
        х2
Out[15] = 9
In[16]:=x = 5
        х2
Out[16] = 5
Out[17] = 25

Заметим, что первый вывод Out[15] по-прежнему дает значение 9, хотя x уже поменялся.

Если хочется, чтобы вывод результата вычисления выражения менялся при изменении входящих в него переменных, можно использовать Dynamic:

In[18] := Dynamic [x2]
Out[18]=x2

Выполним следующие команды и обратим внимание на то, как будет меняться вывод предыдущей, т.е. Out[18] команды:

In[19]: = x = 7;
Out[18] = 49
In[20]:=x = ∫y d y;
Out[18]=y4/4
In[21]:=x = Plot[x2, {x,  -1, 1}];

Динамика и элементы управления. Сам по себе ползунок не влияет на значение аргумента x:

In[22]: = х = 0.5;
In[23] := Slider [x]

In[24]: = x
Out[24] = 0.5

Если ползунок использовать вместе с Dynamic, то переменная x будет динамически обновлять свое значение при перемещении ползунка:

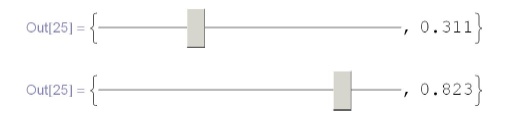
In[25]:={Slider [Dynamic [x] ] , Dynamic [x]}

In[26]: = x 
Out[26] = 0.5

Приведем примеры использования динамики вместе с двумерным ползунком:

In[27] :={Slider2D [Dynamic [x] ] , Dynamic [x]}

In[28] := {Slider [Dynamic [k] ] ,
            Dynamic [Plot [Sin [k x] , {x, 0, 20π } ,
              PlotRange -> {{0, 20 π} ,{-1, 1}}]]}

Теперь сдвинем слайдер:

In[29] :={Slider2D [Dynamic [r] ] ,
           Dynamic[Plot3D[Cos[Norm[{x, y} - r] ] , {x, 0, 1}, 
            {y, 0, 1}, Mesh -> None] ]}

Приведем примеры использования динамики вместе с другими элементами управления:

In[30] : = Clear [x]
             {Manipulator[Dynamic[xl]], Dynamic[xl]} 
             {Checkbox[Dynamic[x2]], Dynamic[x2]} 
            Map[RadioButton[Dynamic[x3], #]  &, {1, 2, 3}] 
              {ColorSlider[Dynamic[col] ] , 
                Dynamic[Graphics[{col, Disk []}]]} 
               p = {0.5, 0.5} ;
               Graphics[Locator[Dynamic[p]], PlotRange -> 1] 
               Dynamic[p]

Out[37] = ImageScaled[ {0.4 8308 9, 0.58 4573} ] 
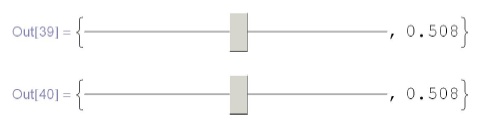
In[38] : = Clear [k, x, xl, x2 , p]

Локализация переменных. В приводимых ниже двух примерах ползунков оба они изменяются одинаково при изменении одного из них (так как x - глобальная переменная).

In[39]:={Slider [Dynamic [x] ] , Dynamic [x]} 
         {Slider[Dynamic[x]], Dynamic[x]}

Чтобы избавиться от такой зависимости, можно локализовать переменную x (по аналогии с тем, как это делалось в Module[] ).

In[41]:= 
      DynamicModule[{х}, {Slider[Dynamic[x]], Dynamic[x]}] 
      DynamicModule[{x}, {Slider[Dynamic[x]], Dynamic[x]}]

Локализация с помощью DynamicModule имеет свои преимущества, в частности, при сохранении проекта и выхода из него текущие значения локализованных переменных сохраняются (этого не происходит со значениями глобальных переменных и локальных переменных из Module ).