Практикум по компьютерной геометрии
[+]
Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1028 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00
ISBN: 978-5-9556-0117-5
Темы: Математика, САПР
Специальности: Математик
Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение
Лекция 1:

Первое знакомство с пакетом Mathematica
A
|
версия для печати
Лекция 1: 123456789 || Лекция 2 >

(4.1) Вычислить кривизну следующих кривых: б) 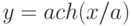y = a ch(x/a).

Решение 1. В качестве параметра выберем x, тогда

\tt In[225]:=$\gamma$[x\_] := \{x, a Cosh$\left[\frac{x}{a}\right]$\};

Найдем натуральный параметр:

\text{In[226]:=}f[x\_]=\int \sqrt{\gamma '[x]. \gamma '[x]} dx}\\ \\ \text{Out[226]=}a \sqrt{Cosh\left[\frac xa\right]^2} Tanh\left[\frac xa\right]\\ \\ \text{In[227]:=}f[x\_]=\text{Simplify}\left[\int \sqrt{\gamma '[x].\gamma '[x]} dx\right]\\ \\ \text{Out[227]=}a\sqrt{Cosh\left[\frac xa\right]^2} Tanh\left[\frac xa\right]

В качестве второго параметра команды

\tt Simplify
можно указать предположения, которые помогут упростить выражение:

\text{In[228]:=}f[x\_]=\text{Simplify}\left[\int\sqrt{\gamma '[x]. \gamma '[x]} dx, \text{ Cosh}\left[\frac xa\right] \ge 0\right] \\ \\ \text{Out[228]=}a Sinh\left[\frac xa\right]

Выразим x через натуральный параметр s:

\tt In[229]:=g[s\_]=InverseFunction[f][s] \\ \\ Out[229]=$f^{(-1)} [s]$

Заменим параметр на натуральный:

\text{In[230]:=}\gamma 1[s\_]=\gamma [x] /. x \to g[s] \\ \\ \text{Out[230]=}\left\{f^{(-1)}[s], a Cosh\left[\frac{f^{(-1)}[s]}{a}\right]\right\} \\ \\ \text{In[231]:=}k[s\_]=\sqrt{\gamma 1''[s].\gamma 1''[s]} \text{// Simplify} \\ \\ \text{Out[231]=}\sqrt{\frac{Sech\left[\frac{f^{-1}[s]}{a}\right]^4}{a^2}}

Выразим x через натуральный параметр s (другой способ):

\tt In[232]:=res=Solve[s == f[x], x] \\ \\ \\ \phantom{In[232]}Solve::ifun: \\ \phantom{In[232]:=}Inverse functions are being used by Solve, so some solutions may not be found; \\ \phantom{In[232]:=res=S}Use Reduce for complete solution information.>> \\ \\ Out[232]=$\left\{\left\{x \to a ArcSinh\left[\frac sa\right]\right\}\right\}$ \\ \\ In[233]:= $\gamma$1[s\_]=$\gamma$[x] /. res[\![1]\!] \\ \\ Out[233]=$\{a ArcSinh[\frac sa], a \sqrt{1+\frac {s^2}{a^2}}\}$ \\ \\ In[234]:=k[s\_]=$\sqrt{\gamma 1''[s].\gamma 1''[s]$ \\ \\ Out[234]=$\sqrt{\frac{s^2}{a^4+\left(1+\frac{s^2}{a^2}\right)^3}+\left(-\frac{s^2}{a^3\left(1+\frac{s^2}{a^2}\right)^{\frac 32}}+\frac{1}{a \sqrt{1+\frac{s^2}{a^2}}}\right)^2}$ \\ \\ In[235]:= k[s\_]=Simplify$\left[\sqrt{\gamma 1''[s]. \gamma 1''[s]}\right]$ \\ \\ Out[235]=$\sqrt{\frac{a^2}{(a^2+s^2)^2}}$ \\ \\ In[236]:=k[s\_]=Simplify$\left[\sqrt{\gamma 1''[s]. \gamma1''[s]}, \left\{a>0, a^2+s^2>0\right\}\right]$ \\ \\ Out[236]=$\frac{a}{a^2+s^2}$

Решение 2. Вновь в качестве параметра выберем x и воспользуемся формулой кривизны произвольно параметризованной кривой. Имеем

\text{In[237]:=}\gamma[x\_]=\left\{x, a Cosh\left[\frac xa\right]\right\}; \\ \phantom{\text{In[237]:=}}k[x\_]=\frac{Abs[Det[\{\gamma '[x], \gamma ''[x]\}]]}{Norm[\gamma '[x]]^3} \\ \\ \text{Out[238]=}\frac{Abs\left[\frac{Cosh\left[\frac xa\right]}{a}\right]}{(1+Abs\left[Sinh\left[\frac xa\right]\right]^2\right)^{\frac 32}} \\ \\ \text{In[239]:=} \\ \phantom{In}k[x\_]=Simplify\left[Abs[Det[\{\gamma'[x], \gamma''[x]\}]]/Norm[\gamma'[x]]^3,\right.\\ \phantom{In[23}\left.\left\{Sinh\left[\frac xa\right] \ge 0, Cosh\left[\frac xa\right] \ge 0, a \ge 0\right\}\right]} \\ \\ \text{Out[239]=}\frac{Sech\left[\frac xa\right]^2}{a}

Проверим, что получился тот же результат:

\tt In[240]:=k[x] /. res[\![1]\!] //Simplify} \\ \\ Out[240]=$\frac{a}{a^2+s^2}$ \\ \\ In[241]:=$\gamma[x]$ \\ \\ Out[241]=$\left\{x, a Cosh\left[\frac xa\right]\right\}
\tt In[242]:= \\ \\ \phantom{In}Module[\{$\gamma$, k, a\}, \\ \\ \phantom{InM}$\gamma$[x\_] := $\left\{$x, a Cosh$\left.\left[\frac xa\right]\right\}$; k[x\_] := $\frac{\text{Sech}\left[\frac xa\right]^2}{a}$; \\ \phantom{InM}Manipulate[\{ \\ \phantom{InMMa}ParametricPlot[$\gamma$[x] /. a$\to$aa, \{ x, -1, 1\}, \\ \phantom{InMMaP}AspectRatio$\to$Automatic, Plotrange$\to$\{\{-1,1\}, \{-0.1,3.5\}\}, \\ \phantom{InMMap}ImageSize$\to$100], \\ \phantom{InMMa}Plot[k[x] /. a$\to$aa, \{x, -1, 1\}, AspectRatio$\to$Automatic, \\ \phantom{InMMap}PlotRange$\to$\{\{-1, 1\}, \{-0.1, 3.5\}\}, ImageSize$\to$100] \\ \phantom{InMM}\}, \\ \phantom{InMM}\{\{aa, 0.36\}, 0.3, 3\}] \\ \phantom{In}]

\tt In[243]:= Clear[$\gamma$, a, $\gamma$1, f, g, res, k]
Дальше >>
Лекция 1: 123456789 || Лекция 2 >

Вопросы и ответы

вопросов: 0