НОУ ИНТУИТ | Моделирование систем. Лекция 6: Построение интервальных оценок параметров вероятностных распределений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3366 / 2059 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2. Интервальная оценка математического ожидания нормально распределенной случайной величины

2.1. Случай с известной дисперсией

Используется статистика

$T(\vec X_n,\mu)=\frac{\bar x -\mu}{\sigma}\sqrt{n},$

( 6.7)

где:

$\mu$ — математическое ожидание нормально распределенной случайной величины с известной дисперсией;

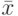$\bar x$ — выборочное среднее выборки объема .

Статистика (6.7) имеет стандартное нормальное распределение и, значит, является центральной статистикой. Так как статистика (6.7) — убывающая функция параметра $\mu$ , то границы доверительного интервала определяются из уравнений

$\frac{\bar x -\mu_i(\bar x_n)}{\sigma}\sqrt{n}=u_{1-\beta},$

( 6.8)

$\frac{\bar x -\mu_{\hat a}(\bar x_n)}{\sigma}\sqrt{n}=u_{\alpha},$

( 6.9)

где $u_{1-\beta}$ , $u_{\alpha}$ — квантили уровней $1-\beta$ и $\alpha$ стандартного нормального распределения.

Поскольку для стандартного нормального закона $u_{1-\alpha}=-u_{\alpha}$ , то с учетом (6.8) и (6.9) имеем нижнюю и верхнюю границы доверительного интервала параметра $\mu$ :

$\mu_i(\bar x_n)=\bar x - \frac{\sigma}{\sqrt{n}}=u_{1-\beta},$

( 6.10)

$\mu_i(\bar x_{\hat a})=\bar x - \frac{\sigma}{\sqrt{n}}=u_{1-\alpha},$

( 6.11)

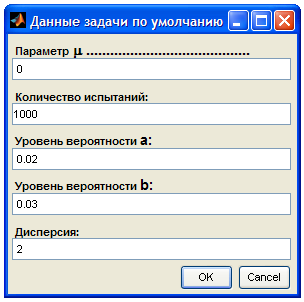
Программный код интервальной оценки математического ожидания:

clear,clc,close all
options.Resize = 'on';
options.WindowStyle='normal';
options.Interpreter='tex';  
D = inputdlg({'\bf Параметр\fontsize{12} \mu .........................................',...
'\bf Количество испытаний: ',...
'\bf Уровень вероятности \fontsize{11}a: ',...
'\bf Уровень вероятности \fontsize{11}b:',...
'\bf Дисперсия:'},'Данные задачи по умолчанию', ...
 1,{' 0','1000',' 0.02',' 0.03',' 2'}, options);

mx = str2num(char(D(1)));
n = str2num(char(D(2)));
a = str2num(char(D(3)));
b = str2num(char(D(4)));
s2 = str2num(char(D(5)));
s = sqrt(s2);
y = 1-a-b;
x = normrnd(mx,s,n,1);
m = mean(x);
u1b = norminv(1-b);
u1a = norminv(1-a);
mn = m-s/sqrt(n)*u1b;
mv = m+s/sqrt(n)*u1a;
LL = [mv mn];
Dlina = abs(max(LL) - min(LL));
d = 'Доверительная вероятность';
fprintf('\n\tИстинное значение параметра: %g\n ',mx)
fprintf('\t%s: %g\n',d,y)
fprintf('\tГраницы доверительного интервала - \n')
na = 'нижняя граница';
nv = 'верхняя граница';
fprintf('\t\t\t\t%s: %g\n',na, mn)
fprintf('\t\t\t\t%s: %g\n',nv,mv)
fprintf('\tДлина доверительного интервала: %g\n',Dlina)
if mx < mn | mx > mv
    fprintf('\n\tИстинное значение параметра не входит в доверительный интервал!\n')
end
%%%------------------ Диаграмма -----------------------
figure(2)
line([mn mn],[0 1],'linew',2,'linestyle',':')
line([mx mx],[0 1],'color','r','linew',1.5)
line([mv mv],[0 1],'linew',2,'linestyle',':')
    if mx < mn
line([mx-1/20, max([mn, mv])+1/20],[0 0],'linew',2,'color','k')
text(mx-1/20,1.15, sprintf('%s','\bf\fontsize{11}Интервальная оценка математического ожидания'))
text(mx-1/20,1.05,sprintf('%s', '\bf\fontsize{11} нормального распределения'))
 
    elseif mx > mv
line([mn-1/20, mx + 1/20],[0 0],'linew',2,'color','k')    
text(mn-1/20,1.15, sprintf('%s','\bf\fontsize{11}Интервальная оценка математического ожидания'))
text(mn-1/20,1.05,sprintf('%s', '\bf\fontsize{11} нормального распределения'))
 
else
line([min([mn, mv]) - 1/20, max([mn, mv]) + 1/10],[0 0],'linew',2,'color','k')    


text(mn-1/20,1.15, sprintf('%s','\bf\fontsize{11}Интервальная оценка математического ожидания'))
text(mn-1/20,1.05,sprintf('%s', '\bf\fontsize{11} нормального распределения'))
 end
 
text(mn,-0.05,'\bf\fontsize{12}\mu_н')
text(mv,-0.05,'\bf\fontsize{12}\mu_в')
text((mn+mv)/2,-0.2,sprintf('%s%g', '\bf\fontsize{12}\mu\fontsize{10}_н = ', mn))
text((mn+mv)/2,-0.3, sprintf('%s%g', '\bf\fontsize{12}\mu\fontsize{10}_и_c_т = ', mx), 'color','r')
text((mn+mv)/2,-0.4, sprintf('%s%g', '\bf\fontsize{12}\mu\fontsize{10}_в = ', mv))
 
ylim([-0.5 1.1])
set(gca,'visible','off')
set(gcf,'color','w')

Возможный результат выполнения программы в командном окне MATLAB

Истинное значение параметра: 0
Доверительная вероятность: 0.95
Границы доверительного интервала 
			нижняя граница: -0.140897
			верхняя граница: 0.0350607
Длина доверительного интервала: 0.175958

Ввод данных программы осуществляется в интерактивном режиме (рис. 6.3). Диаграмма доверительного интервала показана на рис. 6.4.

Рис. 6.3. Диалоговое окно ввода данных

Рис. 6.4. Диаграмма доверительного интервала

Задание 2

Для фиксированных значений входных данных вышеприведенной программы рассчитайте частоту попадания истинного значения параметра в доверительный интервал при следующих объемах выборок (в соответствии с номером компьютера):
```
№ 1: n = 100; № 2: n = 120; № 3: n = 130; № 4: n = 140; № 5: n = 150;
№ 6: n = 160; № 7: n = 170; № 8: n = 180; № 9: n = 200; № 10: n = 210.
```

Значение $\mu$ выберите из интервалов по равномерному закону (в соответствии с номером компьютера):

№ 1: (–1, +1); № 2: (–2.9,  –2); № 3: (–3.9, –3); № 4: (–4.9, –4); № 5: (0.5, 1.59);
№ 6: (2.6, 4.69); № 7: (6.7, 7.79); № 8: (8, 11.8): № 9: (9, 11.9); № 10: (10, 12).

Доверительную вероятность 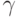$\gamma$ примите равной (в зависимости от номера компьютера)
№ 1: $\gamma=0.91$ ; № 2: $\gamma=0.92$ ; № 3: $\gamma=0.93$ ; № 4: $\gamma=0.94$ ; № 5: $\gamma=0.95$ ;

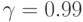№ 6: $\gamma=0.96$ ; № 7: $\gamma=0.97$ ; № 8: $\gamma=0.98$ ; № 9: $\gamma=0.99$ ; № 10: $\gamma=0.995$ .

2.2. Случай с неизвестной дисперсией

Вводится статистика

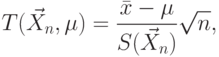$T(\vec X_n,\mu)=\frac{\bar x -\mu}{S(\vec X_n)}\sqrt{n},$

( 6.12)

где:

$\mu$ — оцениваемое математическое ожидание;

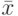$\bar x$ — выборочное среднее для данного объема выборки случайных чисел с произвольным нормальным законом распределения;

$S(\vec X_n)$ — исправленное выборочное среднеквадратическое отклонение для данной выборки. Статистика (6.12) является центральной и распределена по закону Стьюдента ( -распределение) с (n-1) степенями свободы.

Плотность распределения Стьюдента есть четная функция, поэтому при определении квантилей можно положить

$t_{\alpha}(n-1)=-t_{1-\alpha}(n-1),$

где $t_{1-\alpha}$ — квантиль -распределения (распределения Стьюдента).

Для вычисления квантили -распределения в системе MATLAB следует воспользоваться функцией tinv (см. $help\mbox{ }tinv$ ).

Задание 3

Напишите программу по определению доверительного интервала и фиксации попадания истинного значения параметра ( $\mu$ ) в доверительный интервал или непопадания.
Для фиксированных значений входных данных выше приведенной программы рассчитайте частоту попадания истинного значения параметра в доверительный интервал при следующих объемах выборок (в соответствии с номером компьютера):
```
№ 1: n = 100; № 2: n = 120; № 3: n = 130; № 4: n = 140; № 5: n = 150;
№ 6: n = 160; № 7: n = 170; № 8: n = 180; № 9: n = 200; № 10: n = 210.
```

Значение $\mu$ выберите из интервалов по равномерному закону (в соответствии с номером компьютера):

№ 1: (–1, +1); № 2: (–2.9,  –2); № 3: (–3.9, –3); № 4: (–4.9, –4); № 5 (0.5, 1.59);
№ 6: (2.6, 4.69); № 7: (6.7, 7.79); № 8: (8, 11.8): № 9: (9, 11.9); № 10: (10, 12).

Доверительную вероятность 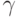$\gamma$ примите равной (в зависимости от номера компьютера)
№ 1: $\gamma=0.91$ ; № 2: $\gamma=0.92$ ; № 3: $\gamma=0.93$ ; № 4: $\gamma=0.94$ ; № 5: $\gamma=0.95$ ;

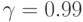№ 6: $\gamma=0.96$ ; № 7: $\gamma=0.97$ ; № 8: $\gamma=0.98$ ; № 9: $\gamma=0.99$ ; № 10: $\gamma=0.995$ .

Контрольные вопросы

Что такое коэффициент доверия?
Что называется квантилью функции распределения случайной величины?
Как связана длина доверительного интервала с доверительной вероятностью при оценке параметра экспоненциального распределения?
В чем смысл применения распределения Стьюдента?
В какой функциональной связи находится интервальная оценка математического ожидания нормально распределенной случайной величины с параметрами интервала и другими параметрами нормального закона?

Дальше >>

Авторизоваться

Моделирование систем

Построение интервальных оценок параметров вероятностных распределений

2. Интервальная оценка математического ожидания нормально распределенной случайной величины

2.1. Случай с известной дисперсией

2.2. Случай с неизвестной дисперсией

Контрольные вопросы

Вопросы и ответы